Với giải sách bài tập Toán 10 Bài 5: Phương trình đường tròn sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:
Giải SBT Toán lớp 10 Bài 5: Phương trình đường tròn
Giải SBT Toán 10 trang 88 Tập 2
Bài 47 trang 88 SBT Toán 10 Tập 2: Phương trình nào sau đây không là phương trình đường tròn?
A. x2+y2=4;
B. x2+y2+2x-1=0;
C. 2x2+3y2+2x+3y=9;
D. x2+y2+4y+3=0.
Lời giải:
Câu A: x2+y2=4 là phương trình đường tròn tâm O(0; 0) bán kính R = 2.
Câu B: x2+y2+2x-1=0(x+1)2+y2=1 là phương trình đường tròn có tâm (-1; 0) bán kính R = .
Câu C: không thể biến đổi về dạng của phương trình đường tròn.
Câu D: x2+y2+4y+3=0x2+(y+2)2=1 là phương trình đường tròn có tâm (0; -2) và bán kính R = 1.
Vậy chọn đáp án C.
A. (8; - 10);
B. (- 8; 10);
C. (- 10; 8);
D. (10; - 8).
Lời giải:
Dễ dàng ta thấy theo dạng phương trình đường tròn (x-a)2+(y-b)2=R2 thì tâm I của (C) có tọa độ là I(-8; 10).
Vậy chọn đáp án B.
A. 4;
B. 16;
C. 2;
D. 1.
Lời giải:
Dễ dàng ta thấy theo dạng phương trình đường tròn (x-a)2+(y-b)2=R2 thì bán kính của đường tròn là R = =2
Vậy chọn đáp án C.
Giải SBT Toán 10 trang 89 Tập 2
A. (x-4)2+(y+2)2=81;
B. (x+4)2+(y-2)2=9;
C. (x-4)2+(y+2)2=9;
D. (x+4)2+(y-2)2=81.
Lời giải:
Đường tròn tâm I(- 4; 2) bán kính R = 9 có phương trình là: (x+4)2+(y-2)2=81
Vậy chọn đáp án D.
A. =(-3;4);
B. =(3;4);
C. =(4;-3);
D. =(4;3).
Lời giải:
Đường tròn có tâm I(3; 4).
Tiếp tuyến tại M của đường tròn có vectơ pháp tuyến là vectơ =(-3;4)
Vậy chọn đáp án A.
A. 16;
B. 8;
C. 4;
D. 256.
Lời giải:
Do M, N chuyển động trên đường tròn nên khoảng cách lớn nhất giữa 2 điểm M, N chính bằng đường kính của đường tròn.
Bán kính của đường tròn (C) là: R==4.
Vậy độ dài lớn nhất của MN = 2R = 8. Chọn đáp án B.
Lời giải:
Ta biến đổi như sau:
x2 + y2 – 6x + 2ky + 2k + 12 = 0
⇔ (x – 3)2 + (y + k)2 = k2 – 2k – 3
Để phương trình trên là phương trình đường tròn thì
k2 – 2k – 3>0
Vậy k < – 1 hoặc k > 3.
Bài 54 trang 89 SBT Toán 10 Tập 2: Viết phương trình đường tròn (C) trong mỗi trường hợp sau:
a) (C) có tâm I(- 6; 2) bán kính 7.
b) (C) có tâm I(3; - 7) và đi qua điểm A(4; 1)
c) (C) có tâm I(1; 2) và tiếp xúc với đường thẳng 3x + 4y + 19 = 0.
d) (C) có đường kính AB với A(- 2; 3) và B(0; 1)
e) (C) có tâm I thuộc đường thẳng :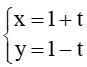
Lời giải:
a) Phương trình (C) có tâm I(- 6; 2) bán kính 7 là: (x + 6)2 + (y – 2)2 = 72.
b) Bán kính của đường tròn (C) là: IA =|| =
Phương trình đường tròn là: (x-3)2+(y+7)2 =65.
c) Bán kính của đường tròn chính bằng khoảng cách từ I đến đường thẳng d: 3x + 4y + 19 = 0.
Suy ra R=d(I,d)= 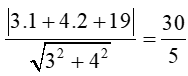
Phương trình đường tròn là: (x -1)2 + (y – 2)2 = 36.
d) Gọi I là tâm của đường tròn thì IA = R và I là trung điểm của AB
Suy ra I(-1; 2), IA =|| =
Phương trình đường tròn là: (x +1)2 + (y – 2)2 = 2.
e) Tâm I thuộc đường thẳng :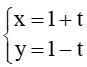
Đường tròn có 2 tiếp tuyến nên khoảng cách từ I đến 2 tiếp tuyến bằng nhau và bằng bán kính của đường tròn.
Ta có: d(I,)=d(I,)
|t-6|=|7t+1|
Với t = thì I và R = d(I; ∆2) = 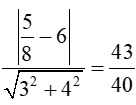
Với t = thì I và R = d(I; ∆2) = 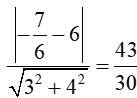
a) ∆ tiếp xúc (C) tại điểm có tung độ bằng 3.
b) ∆ vuông góc với đường thẳng 5x – 12y + 1 = 0.
c) ∆ đi qua điểm D(0; 4).
Lời giải:
Đường tròn có tâm I(-2; 3) và bán kính R = 2.
a) Hoành độ của điểm có tung độ bằng 3 là:
(x+2)2+(3-3)2=4
Suy ra ta có 2 điểm M(0; 3) và điểm N(-4; 3).
Vectơ pháp tuyến của đường thẳng IM là: =(2;0).
Phương trình đường thẳng IM: 2(x – 0) = 0 hay x = 0.
Vectơ pháp tuyến của đường thẳng IN là: =(-2;0).
Phương trình đường thẳng IN: - 2(x + 4) = 0 hay x + 4 = 0.
Vậy phương trình đường thẳng là: x = 0 hoặc x + 4 = 0.
b) ∆ vuông góc với đường thẳng 5x – 12y + 1 = 0
nên ∆ có dạng: 12x + 5y + c = 0.
Khoảng cách từ I đến ∆ bằng R nên d(I,∆)=2
Với c = 35 thì phương trình tiếp tuyến là: 12x + 5y + 35 =0
Với c = - 17 thì phương trình tiếp tuyến là: 12x + 5y – 17 =0
c) Gọi H(a ;b) là tiếp điểm.
Do D(0; 4) thuộc nên DH vuông góc với IH và IH = R = 2.
Ta có: =(a;b-4) và =(a+2;b-3)
⇒ IH = ||==2
⇔ a2 + 4a + 4 + b2 – 6b + 9 = 4
⇔ a2 + 4a + b2 – 6b + 9 = 0 (1)
Ta lại có: .=0 a(a+2)+(b-4)(b-3)=0
⇔ a2 + 2a + b2 – 7b + 12 = 0 (2)
Từ (1) và (2) ta có hệ phương trình:
Với a = 0, b = 3 thì H(0; 3)
Suy ra =(2;0)
Do đó phương trình tiếp tuyến cần tìm là: 2(x – 0) = 0 ⇔ x = 0.
Với a=; b=
Suy ra =
Do đó phương trình tiếp tuyến cần tìm là: 3(x – 0) + 4(y – 4) = 0 ⇔ 3x + 4y – 16 = 0.
Vậy có hai đường thẳng ∆ thỏa mãn yêu cầu là x = 0 hoặc 3x + 4y – 16 = 0.
a) Xác định vị trí tương đối của điểm A đối với đường tròn (C).
b) Đường thẳng d thay đổi đi qua A cắt đường tròn tại M và N. Viết phương trình đường thẳng d sao cho MN ngắn nhất.
Lời giải:
a) Đường tròn (C) có tâm I(-2; 4) và bán kính R = = 5.
Ta có: IA=||= < 5
Do đó A nằm trong đường tròn (C).
b) Dây cung MN ngắn nhất khi khoảng cách từ tâm I đến dây cung là lớn nhất
Do d đi qua A cố định nên khi d thay đổi thì khoảng cách lớn nhất từ I đến d chính bằng IA.
Hay IA vuông góc với d.
Vectơ pháp tuyến của đường thẳng d: =(1;-1)
Phương trình đường thẳng d: (x + 1) – (y – 3) = 0 ⇔ x – y + 4 = 0.
Giải SBT Toán 10 trang 90 Tập 2
Lời giải:
Đường tròn (C) có tâm I(-3; 1) và bán kính R = 3.
Ta có: d(I,)=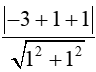
d(I,)=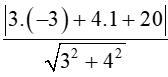
d(I,)=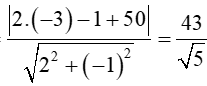
Lời giải:
Gọi H là hình chiếu của M lên ∆
Suy ra MH là khoảng cách từ M đến ∆
MH = 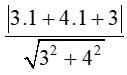
Xét tam giác MNH vuông tại H có:
MN =
Mà R = MN =
Phương trình đường tròn là: (x-1)2 +(y-1)2 =.
Xem thêm các bài giải SBT Toán 10 Cánh diều hay, chi tiết khác:
SBT Toán 10 Bài 3: Phương trình đường thẳng
SBT Toán 10 Bài 5: Phương trình đường tròn
SBT Toán 10 Bài 6: Ba đường conic
SBT Toán 10 Bài tập cuối chương 7