Với giải Bài 8 trang 58 Toán lớp 7 Chân trời sáng tạo chi tiết trong Bài 2: Tam giác bằng nhau giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Bài 2: Tam giác bằng nhau

Bài 8 trang 58 Toán lớp 7 Tập 2: Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng:

a) AD = BC.

b) $△$EAB = $△$ECD.

c) OE là tia phân giác của góc xOy.

Lời giải:

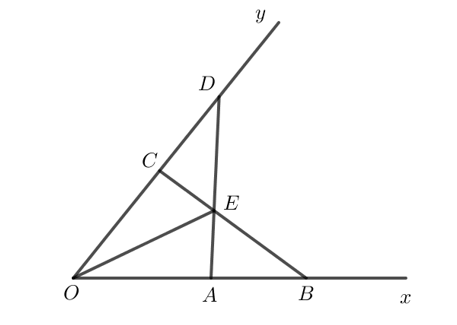
a) Xét hai tam giác OAD và OCB có:

OA = OC (theo giả thiết).

$\hat{O}$chung.

OD = OB (theo giả thiết).

Do đó $△$OAD = $△$OCB (c.g.c).

Suy ra AD = BC (2 cạnh tương ứng).

b) Do OA = OC, OB = OD nên OB - OA = OD - OC hay AB = CD.

Do $△$OAD = $△$OCB (c.g.c) nên $\widehat{O\text{D}A}=\widehat{OBC}$(2 góc tương ứng).

$\widehat{EC\text{D}}$là góc ngoài tại đỉnh C của tam giác OBC nên $\widehat{EC\text{D}}=\widehat{COB}+\widehat{OBC}$(1).

$\widehat{EAB}$là góc ngoài tại đỉnh A của tam giác OAD nên $\widehat{EAB}=\widehat{AOD}+\widehat{ODA}$(2).

Từ (1) và (2) suy ra $\widehat{EC\text{D}}=\widehat{E\text{A}B}$.

Xét hai tam giác EAB và ECD có:

$\widehat{E\text{A}B}=\widehat{EC\text{D}}$(chứng minh trên).

AB = CD (chứng minh trên).

$\widehat{EBA}=\widehat{E\text{DC}}$(chứng minh trên).

Do đó $△$EAB = $△$ECD (g.c.g).

c) Do $△$EAB = $△$ECD (g.c.g) nên BE = DE (2 cạnh tương ứng).

Xét hai tam giác ODE và OBE có:

OD = OB (theo giả thiết).

OE chung.

DE = BE (theo giả thiết).

Do đó $△$ODE = $△$OBE (c.c.c).

Suy ra $\widehat{EOD}=\widehat{EOB}$(2 góc tương ứng).

Vậy OE là tia phân giác của $\widehat{xOy}$.