Với giải Bài 7 trang 98 SGK Toán lớp 10 Cánh diều chi tiết trong Bài 6: Tích vô hướng của hai vectơ giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SGK Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 6: Tích vô hướng của hai vectơ

Bài 7 trang 98 Toán lớp 10: Một máy bay đang bay từ hướng đông sang hướng tây với tốc độ 700 km/h thì gặp luồng gió thổi từ hướng đông bắc sang hướng tây nam với tốc độ 40 km/h (Hình 68). Máy bay bị thay đổi vận tốc sau khi gặp gió thổi.

Tìm tốc độ mới của máy bay (làm tròn kết quả đến hàng phần trăm theo đơn vị km/h).

Lời giải:

Giả sử vận tốc của máy bay theo hướng đông sang tây là $\overrightarrow{v_1}$, vận tốc của luồng gió theo hướng đông bắc sang tây nam là $\overrightarrow{v_2}$ và vận tốc mới của máy bay chính là $\overrightarrow{v}$ thỏa mãn $\overrightarrow{v}=\overrightarrow{v_1}+\overrightarrow{v_2}$.  Ta cần tính độ dài vectơ $\overrightarrow{v}$. 

Theo bài ra ta có: $\left|\overrightarrow{v_1}\right|=700$km/h, $\left|\overrightarrow{v_2}\right|=40$ km/h, $\left(\overrightarrow{v_1},\overrightarrow{v_2}\right)=45°$.

Biểu diễn bài toán như hình vẽ dưới đây:

Khi đó ta có: ABCD là hình bình hành có $\widehat{ABC}=45°$. 

Suy ra: $\widehat{DAB}=180°-45°=135°$; $AD=\left|\overrightarrow{v_2}\right|=40$, $AB=\left|\overrightarrow{v_1}\right|=700$. 

Ta cần tính độ dài đoạn thẳng BD, đây chính là độ dài vectơ $\overrightarrow{v}$. 

Áp dụng định lí sin trong tam giác ABD, ta có: 

BD² = AD² + AB² – 2 . AD . AB . cosA

          = 40² + 700² – 2 . 40 . 700 . cos135°

          ≈ 531 197, 98

Suy ra BD ≈ 728,83 (km/h). 

Vậy tốc độ mới của máy bay sau khi gặp gió thổi là 728,83 km/h. 

Bài tập vận dụng:

Bài 1. Cho đoạn thẳng AB có trung điểm O, điểm M tùy ý khác O, A, B và không thuộc AB, biết 4OM² = AB². Sử dụng các kiến thức về vectơ, chứng minh MA ⊥ MB.

Hướng dẫn giải:

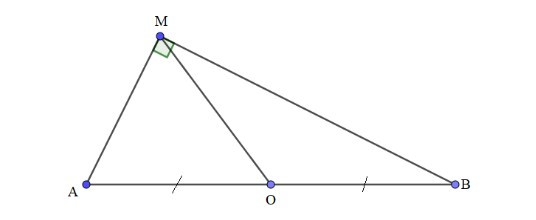
Ta có:

4OM² = AB² ⟺ (2OM)² = AB²

⇔ ${\left(2\overrightarrow{\mathrm{OM}}\right)}^2={\overrightarrow{\mathrm{AB}}}^2$

⇔ ${\left(\overrightarrow{\mathrm{MA}}+\overrightarrow{\mathrm{MB}}\right)}^2={\left(\overrightarrow{\mathrm{AM}}+\overrightarrow{\mathrm{MB}}\right)}^2$ 

⇔ ${\overrightarrow{\mathrm{MA}}}^2+2\overrightarrow{\mathrm{MA}}.\overrightarrow{\mathrm{MB}}+{\overrightarrow{\mathrm{MB}}}^2={\overrightarrow{\mathrm{AM}}}^2+2\overrightarrow{\mathrm{AM}}.\overrightarrow{\mathrm{MB}}+{\overrightarrow{\mathrm{MB}}}^2$

⇔ ${\left|\overrightarrow{\mathrm{MA}}\right|}^2+2\overrightarrow{\mathrm{MA}}.\overrightarrow{\mathrm{MB}}+{\left|\overrightarrow{\mathrm{MB}}\right|}^2={\left|\overrightarrow{\mathrm{AM}}\right|}^2+2\overrightarrow{\mathrm{AM}}.\overrightarrow{\mathrm{MB}}+{\left|\overrightarrow{\mathrm{MB}}\right|}^2$

⇔ ${\mathrm{MA}}^2+2\overrightarrow{\mathrm{MA}}.\overrightarrow{\mathrm{MB}}+{\mathrm{MB}}^2={\mathrm{AM}}^2+2\overrightarrow{\mathrm{AM}}.\overrightarrow{\mathrm{MB}}+{\mathrm{MB}}^2$

⇔ ${\mathrm{MA}}^2+2\overrightarrow{\mathrm{MA}}.\overrightarrow{\mathrm{MB}}+{\mathrm{MB}}^2={\mathrm{AM}}^2-2\overrightarrow{\mathrm{MA}}.\overrightarrow{\mathrm{MB}}+{\mathrm{MB}}^2$

⇔ $4\overrightarrow{\mathrm{MA}}.\overrightarrow{\mathrm{MB}}=0$

⇔ $\overrightarrow{\mathrm{MA}}.\overrightarrow{\mathrm{MB}}=0$

⇒ $\overrightarrow{\mathrm{MA}}\perp \overrightarrow{\mathrm{MB}}$ ⇒ MA ⊥ MB (đpcm).

Bài 2. Cho tam giác ABC bất kì có I là trung điểm của AB. Chứng minh đẳng thức:

CA² + CB² = 2CI² + $\frac{{\mathrm{AB}}^2}{2}$.

Hướng dẫn giải:

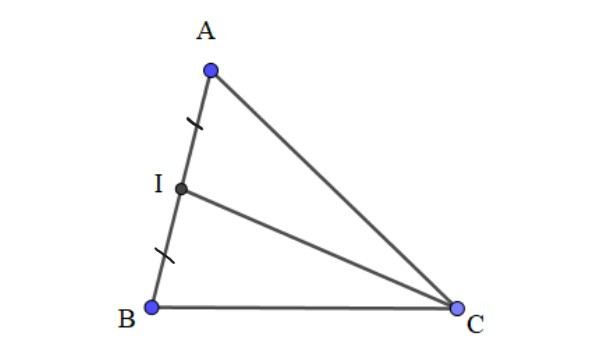
Ta có:

VP = 2CI² + $\frac{{\mathrm{AB}}^2}{2}$

⇔ 2VP = 4CI² + AB²

⇔ 2VP= (2CI)² + AB²

⇔ 2VP =  ${\left(2\overrightarrow{\mathrm{CI}}\right)}^2+{\overrightarrow{\mathrm{AB}}}^2$

⇔ 2VP = ${\left(\overrightarrow{\mathrm{CA}}+\overrightarrow{\mathrm{CB}}\right)}^2+{\left(\overrightarrow{\mathrm{AC}}+\overrightarrow{\mathrm{CB}}\right)}^2$  

⇔ 2VP = ${\overrightarrow{\mathrm{CA}}}^2+2\overrightarrow{\mathrm{CA}}.\overrightarrow{\mathrm{CB}}+{\overrightarrow{\mathrm{CB}}}^2+{\overrightarrow{\mathrm{AC}}}^2+2\overrightarrow{\mathrm{AC}}.\overrightarrow{\mathrm{CB}}+{\overrightarrow{\mathrm{CB}}}^2$

⇔ 2VP = ${\overrightarrow{\mathrm{CA}}}^2+2\overrightarrow{\mathrm{CA}}.\overrightarrow{\mathrm{CB}}+{\overrightarrow{\mathrm{CB}}}^2+{\overrightarrow{\mathrm{AC}}}^2-2\overrightarrow{\mathrm{CA}}.\overrightarrow{\mathrm{CB}}+{\overrightarrow{\mathrm{CB}}}^2$

⇔ 2VP = $2{\overrightarrow{\mathrm{CA}}}^2+2{\overrightarrow{\mathrm{CB}}}^2$

⇔ 2VP = $2{\mathrm{CA}}^2+2{\mathrm{CB}}^2$= VT

⇒ CA² + CB² = 2CI² + $\frac{{\mathrm{AB}}^2}{2}$(đpcm).

Bài 3. Cho tam giác ABC, biết AB = a, AC = 2a, $\widehat{\mathrm{A}}$= 60°. Sử dụng các kiến thức về vectơ, tính độ dài cạnh BC.

Hướng dẫn giải:

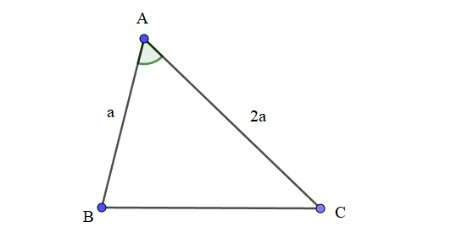
Áp dụng quy tắc hiệu hai vectơ ta có:

$\overrightarrow{\mathrm{BC}}=\overrightarrow{\mathrm{AC}}-\overrightarrow{\mathrm{AB}}$

⇒ ${\overrightarrow{\mathrm{BC}}}^2={\left(\overrightarrow{\mathrm{AC}}-\overrightarrow{\mathrm{AB}}\right)}^2$= ${\overrightarrow{\mathrm{AC}}}^2-2\overrightarrow{\mathrm{AC}}.\overrightarrow{\mathrm{AB}}+{\overrightarrow{\mathrm{AB}}}^2$

Ta có:

${\overrightarrow{\mathrm{AC}}}^2={\left|\overrightarrow{\mathrm{AC}}\right|}^2$= AC² = (2a)² = 4a²

${\overrightarrow{\mathrm{AB}}}^2={\left|\overrightarrow{\mathrm{AB}}\right|}^2$= AB² = a²

$\overrightarrow{\mathrm{AC}}.\overrightarrow{\mathrm{AB}}$ = $\left|\overrightarrow{\mathrm{AC}}\right|.\left|\overrightarrow{\mathrm{AB}}\right|.\cos \left(\overrightarrow{\mathrm{AC}},\overrightarrow{\mathrm{AB}}\right)$ = AC.AB.cos$\widehat{\mathrm{BAC}}$ = 2a.a.cos60° = 2.a.a.$\frac{1}{2}$ = a²

⇒ ${\overrightarrow{\mathrm{BC}}}^2$= 4a² – 2a² + a² = 3a²

⇒ BC² = ${\left|\overrightarrow{\mathrm{BC}}\right|}^2$ = ${\overrightarrow{\mathrm{BC}}}^2$= 3a²

⇒ BC = $\sqrt{3{\mathrm{a}}^2}$= $\mathrm{a}\sqrt{3}$.