Với giải Luyện tập 1 trang 93 SGK Toán lớp 10 Cánh diều chi tiết trong Bài 6: Tích vô hướng của hai vectơ giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SGK Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 6: Tích vô hướng của hai vectơ
Luyện tập 1 trang 93 Toán lớp 10: Cho tam giác ABC vuông tại A có, AB = 3 cm. Tính.
Lời giải:
Ta có tam giác ABC vuông ở A nên
.
Lại có: tan B = ⇒ AC = AB . tan0B = 3 . tan 30° = .
Và sin B = ⇒ BC = .
Ta có: = = .
= = = 6 . cos 60° = 3.
Vậy và .
Lý thuyết Định nghĩa
1.1. Tích vô hướng của hai vectơ có cùng điểm đầu
– Góc giữa hai vectơ , là góc giữa hai tia OA, OB và được kí hiệu là
– Tích vô hướng của hai vectơ và là một số thực, kí hiệu là ., được xác định bởi công thức: .
Ví dụ: Cho tam giác ABC đều cạnh 2a có đường cao AH. Tính tích vô hướng của .
Hướng dẫn giải:
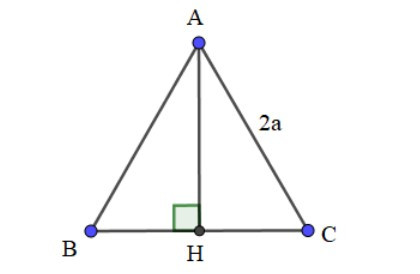
Vì tam giác ABC đều nên = 60°
⇒ = = 60°
Ta có:
=
⇒ = AB.AC.cos = AB.AC.cos60° = 2a.2a. = 2a2.
1.2. Tích vô hướng của hai vectơ tùy ý
Định nghĩa:
Cho hai vectơ , khác Lấy một điểm O và vẽ vectơ (Hình vẽ).
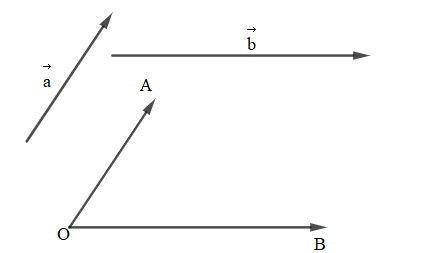
+ Góc giữa hai vectơ , , kí hiệu , là góc giữa hai vectơ , .
+ Tích vô hướng của hai vectơ và , kí hiệu . là tích vô hướng của hai vectơ và . Như vậy, tích vô hướng của hai vectơ và là một số thực được xác định bởi công thức: . = .
Quy ước: Tích vô hướng của một vectơ bất kì với vectơ là số 0.
Chú ý:
+) =
+) Nếu = 90° thì ta nói hai vectơ , vuông góc với nhau, kí hiệu ⊥ hoặc ⊥ . Khi đó . = = 0.
+) Tích vô hướng của hai vectơ cùng hướng bằng tích hai độ dài của chúng.
+) Tích vô hướng của hai vectơ ngược hướng bằng số đối của tích hai độ dài của chúng.
Ví dụ: Cho tam giác vuông cân ABC có AB = AC = a. Tính các tích vô hướng ,.
Hướng dẫn giải:
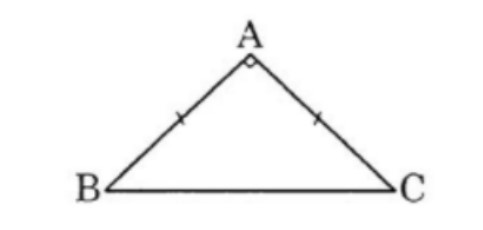
+ Vì tam giác ABC vuông cân, mà AB = AC
⇒ Tam giác ABC vuông cân tại A.
⇒ AB ⊥ AC
⇒ = = = 0
+ Ta có: BC = = = a.
⇒ = = a. a.cos135° = a. a. = –a2.
Xem thêm lời giải bài tập SGK Toán 10 Cánh diều hay, chi tiết khác:
Luyện tập 1 trang 93 Toán lớp 10: Cho tam giác ABC vuông tại A có, AB = 3 cm. Tính.....
Luyện tập 2 trang 95 Toán lớp 10: Cho tam giác ABC đều cạnh a, AH là đường cao. Tính:....
Luyện tập 3 trang 96 Toán lớp 10: Chứng minh rằng với hai vectơ bất kì , ta có:.....
Bài 1 trang 97 Toán lớp 10: Nếu hai điểm M, N thỏa mãn thì độ dài đoạn thẳng MN bằng bao nhiêu?.....
Bài 2 trang.98 Toán lớp 10: Phát biểu nào sau đây là đúng?......
Bài 3 trang 98 Toán lớp 10: Tính trong mỗi trường hợp sau:...
Bài 4 trang 98 Toán lớp 10: Cho hình vuông ABCD cạnh a. Tính các tích vô hướng sau:...
Bài 5 trang 98 Toán lớp 10: Cho tam giác ABC. Chứng minh:....
Bài 6 trang 98 Toán lớp 10: Cho tam giác nhọn ABC, kẻ đường cao AH. Chứng minh rằng:...
Xem thêm các bài giải SGK Toán 10 Cánh diều hay, chi tiết khác:
Bài 5: Tích của một số với một vectơ
Bài 6: Tích vô hướng của hai vectơ
Bài 1: Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây
Giải SGK Toán 10 Bài 2: Hoán vị. Chỉnh hợp