Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài 1: Tọa độ của vectơ chi tiết sách Toán 10 Tập 2 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài 1: Tọa độ của vectơ

Giải Toán 10 trang 60 Tập 2

Câu hỏi khởi động trang 60 Toán lớp 10 Tập 2: Hình 1 minh họa hoạt động của một màn hình ra đa ở trạm kiểm soát không lưu của sân bay, đang theo dõi một máy bay hạ cánh. Máy bay xuất hiện trên màn hình ra đa bởi một đốm sáng, kí hiệu là M. Dựa trên sự thay đổi của tọa độ vectơ $\overrightarrow{OM}$ , trạm kiểm soát có thể xác định được đường bay của máy bay.

Tọa độ của vectơ $\overrightarrow{OM}$ là gì?

Lời giải:

Sau bài học này ta sẽ biết tọa độ của vectơ $\overrightarrow{OM}$ chính là tọa độ của điểm M.

I. Tọa độ của một điểm

Hoạt động 1 trang 60 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy (Hình 2), hãy:

a) Tìm hoành độ và tung độ của điểm A.

b) Nêu cách xác định tọa độ của điểm M tùy ý.

Lời giải:

a) Từ điểm A, kẻ đường thẳng vuông góc với trục hoành và ta thấy đường thẳng này cắt trục hoành tại điểm ứng với số 2. Tương tự, từ A kẻ đường thẳng vuông góc với trục tung và ta thấy đường thẳng này cắt trục tung tại điểm ứng với số 2.

Vậy hoành độ của điểm A là 2 và tung độ của điểm A là 2.

b) Để xác định tọa độ của một điểm M tùy ý trong mặt phẳng tọa độ Oxy, ta làm như sau:

- Từ M kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm H ứng với số a. Số a là hoành độ của điểm M.

- Từ M kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm K ứng với số b. Số b là tung độ của điểm M.

Cặp số (a; b) là tọa độ của điểm M trong mặt phẳng tọa độ Oxy. Ta kí hiệu là M(a; b).

II. Tọa độ của một vectơ

Giải Toán 10 trang 61 Tập 2

Hoạt động 2 trang 61 Toán lớp 10 Tập 2: Cho điểm M trong mặt phẳng tọa độ Oxy.

a) Vẽ vectơ $\overrightarrow{OM}$.

b) Nêu cách xác định tọa độ của điểm M.

Lời giải:

a) Ta vẽ vectơ $\overrightarrow{OM}$ như sau:

b) Để xác định tọa độ của một điểm M trong mặt phẳng tọa độ Oxy, ta làm như sau:

- Từ M kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm H ứng với số a. Số a là hoành độ của điểm M.

- Từ M kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm K ứng với số b. Số b là tung độ của điểm M.

Cặp số (a; b) là tọa độ của điểm M trong mặt phẳng tọa độ Oxy. Ta kí hiệu là M(a; b).

Hoạt động 3 trang 61 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho vectơ (Hình 7). Hãy xác định điểm A sao cho $\overrightarrow{OA}=\overrightarrow{u}$.

Lời giải:

Để xác định điểm A, ta làm như sau:

- Qua O kẻ đường thẳng d song song với giá của vectơ $\overrightarrow{u}$.

- Lấy điểm A trên đường thẳng d sao cho hai vectơ $\overrightarrow{OA},\overrightarrow{u}$ cùng hướng và độ dài đoạn thẳng OA bằng độ dài vectơ $\overrightarrow{u}$.

Vậy ta xác định được điểm A thỏa mãn yêu cầu.

Giải Toán 10 trang 62 Tập 2

Luyện tập 1 trang 62 Toán lớp 10 Tập 2: Tìm tọa độ của các vectơ $\overrightarrow{c},\overrightarrow{d}$ trong Hình 11.

Lời giải:

- Giá của vectơ $\overrightarrow{c}$ song song với trục Ox, trên trục Ox, lấy điểm A sao cho hai vectơ $\overrightarrow{OA},\overrightarrow{c}$ cùng hướng và độ dài đoạn thẳng OA bằng độ dài vectơ $\overrightarrow{c}$ và bằng 3 (đơn vị ô vuông).

Ta có: $\overrightarrow{c}=\overrightarrow{OA}$ và A(– 3; 0); tọa độ vectơ $\overrightarrow{OA}$ chính là tọa độ điểm A nên $\overrightarrow{c}=\left(-3;0\right)$ .

- Giá của vectơ $\overrightarrow{d}$ song song với trục Oy, trên trục Oy, lấy điểm B sao cho hai vectơ $\overrightarrow{OB},\overrightarrow{d}$ cùng hướng và độ dài đoạn thẳng OB bằng độ dài vectơ $\overrightarrow{d}$ và bằng 2 (đơn vị ô vuông).

Ta có: $\overrightarrow{d}=\overrightarrow{OB}$ và B(0; 2); tọa độ vectơ $\overrightarrow{OB}$ chính là tọa độ điểm B nên $\overrightarrow{d}=\left(0;2\right)$.

Giải Toán 10 trang 63 Tập 2

Hoạt động 4 trang 63 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho vectơ$\overrightarrow{u}=\left(a;b\right)$. Ta chọn điểm A sao cho$\overrightarrow{OA}=\overrightarrow{u}$.

Xét vectơ đơn vị $\overrightarrow{i}$ trên trục hoành Ox và vectơ đơn vị $\overrightarrow{j}$ trên trục tung Oy (Hình 12).

a) Tìm hoành độ và tung độ của điểm A.

b) Biểu diễn vectơ $\overrightarrow{OH}$ qua vectơ $\overrightarrow{i}$.

c) Biểu diễn vectơ $\overrightarrow{OK}$ qua vectơ $\overrightarrow{j}$.

d) Chứng tỏ rằng $\overrightarrow{u}=a\overrightarrow{i}+b\overrightarrow{j}$.

Lời giải:

a) Ta có: $\overrightarrow{OA}=\overrightarrow{u}$, mà (a; b) là tọa độ của vectơ $\overrightarrow{u}$ nên điểm A có hoành độ là a và tung độ là b.

b) Điểm H biểu diễn số a trên trục Ox nên $\overrightarrow{OH}=a\overrightarrow{i}$.

c) Điểm K biểu diễn số b trên trục Oy nên $\overrightarrow{OK}=b\overrightarrow{j}$.

d) Áp dụng quy tắc hình bình hành ta có: $\overrightarrow{OA}=\overrightarrow{OK}+\overrightarrow{OH}$.

Mà $\overrightarrow{OH}=a\overrightarrow{i}$,$\overrightarrow{OK}=b\overrightarrow{j}$ nên $\overrightarrow{OA}=a\overrightarrow{i}+b\overrightarrow{j}$.

Theo bài ra ta có: $\overrightarrow{OA}=\overrightarrow{u}$.

Vậy $\overrightarrow{u}=a\overrightarrow{i}+b\overrightarrow{j}$.

Luyện tập 2 trang 63 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho điểm B(– 1; 0) và vectơ $\overrightarrow{v}$ = (0; – 7).

a) Biểu diễn $\overrightarrow{v}$ vectơ qua hai vectơ $\overrightarrow{i}$ và $\overrightarrow{j}$.

b) Biểu diễn $\overrightarrow{OB}$ vectơ qua hai vectơ $\overrightarrow{i}$ và $\overrightarrow{j}$.

Lời giải:

a) Vì $\overrightarrow{v}$ = (0; – 7) nên$\overrightarrow{v}=0.\overrightarrow{i}+\left(-7\right).\overrightarrow{j}=-7\overrightarrow{j}$.

b) Vì điểm B có tọa độ là (– 1; 0) nên $\overrightarrow{OB}=\left(-1;0\right)$. Do đó:

$\overrightarrow{OB}=\left(-1\right).\overrightarrow{i}+0.\overrightarrow{j}=-\overrightarrow{i}$.

III. Liên hệ giữa tọa độ của điểm và tọa độ của vectơ

Giải Toán 10 trang 64 Tập 2

Hoạt động 5 trang 64 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho hai điểm A, B (Hình 13).

a) Tìm hoành độ x_A và tung độ y_A­ của điểm A; hoành độ x_B và tung độ y_B của điểm B.

b) Tìm điểm M sao cho $\overrightarrow{OM}=\overrightarrow{AB}$ . Từ đó, tìm hoành độ a và tung độ b của vectơ $\overrightarrow{AB}$ .

c) So sánh: x_B – x_A và a; y_B – y_A và b.

Lời giải:

a) Từ A và B ta kẻ các đường thẳng vuông góc với trục tung và trục hoành.

Ta xác định được tọa độ của các điểm A và B.

Hoành độ của điểm A là x_A = 2, tung độ của điểm A là y_A = 2.

Hoành độ của điểm B là x_B = 4, tung độ của điểm B là y_B = 3.

b) Để xác định điểm M, ta làm như sau:

- Từ đểm O, kẻ đường thẳng d song song với giá của vectơ $\overrightarrow{AB}$ (chính là đường thẳng AB).

- Lấy điểm M trên đường thẳng d sao cho hai vectơ $\overrightarrow{AB},\overrightarrow{OM}$ cùng hướng và độ dài đoạn thẳng OM bằng độ dài vectơ $\overrightarrow{AB}$ (chính là độ dài đoạn thẳng AB).

Ta xác định được điểm M thỏa mãn $\overrightarrow{OM}=\overrightarrow{AB}$ như hình vẽ:

Từ điểm M, kẻ đường thẳng vuông góc với trục hoành, đường thẳng này cắt trục hoành tại điểm ứng với số 2, nên hoành độ của điểm M là x_M = 2.

Từ điểm M, kẻ đường thẳng vuông góc với trục tung, đường thẳng này cắt trục tung tại điểm ứng với số 1, nên tung độ của điểm M là y_M = 1.

Tọa độ của điểm M chính là tọa độ của vectơ $\overrightarrow{OM}$ nên $\overrightarrow{OM}=\left(2;1\right)$.

Lại có $\overrightarrow{OM}=\overrightarrow{AB}$ , do đó tọa độ của vectơ $\overrightarrow{AB}$ là (2; 1).

Vậy hoành độ của vectơ $\overrightarrow{AB}$ là a = 2 và tung độ của vectơ $\overrightarrow{AB}$ là b = 1.

c) Ta có: x_B – x_A = 4 – 2 = 2 và a = 2 nên x_B – x_A = a.

Và y_B – y_A = 3 – 2 = 1 và b = 1 nên y_B – y_A = b.

Luyện tập 3 trang 64 Toán lớp 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho các điểm: A(1; 3), B(5; – 1), C(2; – 2), D(– 2; 2).

Chứng minh $\overrightarrow{AB}=\overrightarrow{DC}$.

Lời giải:

Ta có: $\overrightarrow{AB}=\left(5-1;\left(-1\right)-3\right)$. Do đó $\overrightarrow{AB}=\left(4;-4\right)$.

Lại có: $\overrightarrow{DC}=\left(2-\left(-2\right);\left(-2\right)-2\right)$. Do đó $\overrightarrow{DC}=\left(4;-4\right)$

Vậy $\overrightarrow{AB}=\overrightarrow{DC}$ .

Bài tập

Giải Toán 10 trang 65 Tập 2

Bài 1 trang 65 Toán lớp 10 Tập 2: Tìm tọa độ của các vectơ trong Hình 16 và biểu diễn mỗi vectơ đó qua hai vectơ $\overrightarrow{i}$và $\overrightarrow{j}$.

Lời giải:

Từ O, vẽ các đường thẳng song song với giá của các vectơ $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c},\overrightarrow{d}$.

Trên các đường thẳng đó, lần lượt lấy các điểm A, B, C, D sao cho $\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$, $\overrightarrow{OC}=\overrightarrow{c}$, $\overrightarrow{OD}=\overrightarrow{d}$ (như hình vẽ trên).

Từ các điểm A, B, C, D, kẻ các đường thẳng vuông góc với các trục tọa độ Ox, Oy để xác định tọa độ các điểm này. Ta xác định được tọa độ của các điểm là: A(– 5; – 3), B(3; – 4), C(– 1; 3) và D(2; 5).

+) Ta có $\overrightarrow{OA}=\overrightarrow{a}$ và tọa độ A là A(– 5; – 3), tọa độ của vectơ $\overrightarrow{OA}$ chính là tọa độ của điểm A, do đó tọa độ của vectơ $\overrightarrow{a}$ là (– 5; – 3) và $\overrightarrow{a}=\left(-5\right).\overrightarrow{i}+\left(-3\right).\overrightarrow{j}=-5\overrightarrow{i}-3\overrightarrow{j}$.

+) Ta có $\overrightarrow{OA}=\overrightarrow{a}$ và tọa độ của B(3; – 4), tọa độ của vectơ $\overrightarrow{OB}$ chính là tọa độ của điểm B, do đó tọa độ của vectơ $\overrightarrow{b}$ là (3; – 4) và $\overrightarrow{b}=3.\overrightarrow{i}+\left(-4\right).\overrightarrow{j}=3\overrightarrow{i}-4\overrightarrow{j}$.

+) Ta có $\overrightarrow{OC}=\overrightarrow{c}$ và tọa độ của C(– 1; 3), tọa độ của vectơ $\overrightarrow{OC}$ chính là tọa độ của điểm C, do đó tọa độ của vectơ $\overrightarrow{c}$ là (– 1; 3) và $\overrightarrow{c}=\left(-1\right).\overrightarrow{i}+3.\overrightarrow{j}=-\overrightarrow{i}+3\overrightarrow{j}$.

+) Ta có $\overrightarrow{OD}=\overrightarrow{d}$ và tọa độ của D(2; 5), tọa độ của vectơ $\overrightarrow{OD}$ chính là tọa độ của điểm D, do đó tọa độ của vectơ $\overrightarrow{d}$ là (2; 5) và $\overrightarrow{d}=2.\overrightarrow{i}+5.\overrightarrow{j}=2\overrightarrow{i}+5\overrightarrow{j}$.

Bài 2 trang 65 Toán lớp 10 Tập 2: Tìm tọa độ của các vectơ sau:

a) $\overrightarrow{a}=3\overrightarrow{i}$;

b) $\overrightarrow{b}=-\overrightarrow{j}$;

c) $\overrightarrow{c}=\overrightarrow{i}-4\overrightarrow{j}$;

d) $\overrightarrow{d}=0,5\overrightarrow{i}+\sqrt{6}\overrightarrow{j}$.

Lời giải:

Bài 3 trang 65 Toán lớp 10 Tập 2: Tìm các số thực a và b sao cho mỗi cặp vectơ sau bằng nhau:

a) $\overrightarrow{u}=\left(2a-1;-3\right)$ và $\overrightarrow{v}=\left(3;4b+1\right)$ ;

b) $\overrightarrow{x}=\left(a+b;-2a+3b\right)$ và $\overrightarrow{y}=\left(2a-3;4b\right)$ .

Lời giải:

Hai vectơ bằng nhau khi hoành độ của vectơ này bằng hoành độ của vectơ kia và tung độ của vectơ này bằng tung độ của vectơ kia.

Từ (1) và (2) ta được: a – 3 = – 2a ⇔ a + 2a = 3 ⇔ 3a = 3 ⇔ a = 1.

Thay vào (1) ta được: b = 1 – 3 = – 2.

Vậy a = 1 và b = – 2.

Giải Toán 10 trang 66 Tập 2

Bài 4 trang 66 Toán lớp 10 Tập 2: Trong mặt phẳng toạ độ Oxy, cho ba điểm A(2; 3), B(– 1; 1), C(3; – 1).

a) Tìm toạ độ điểm M sao cho $\overrightarrow{AM}=\overrightarrow{BC}$ .

b) Tìm toạ độ trung điểm N của đoạn thẳng AC. Chứng minh rằng $\overrightarrow{BN}=\overrightarrow{NM}$.

Lời giải:

Bài 5 trang 66 Toán lớp 10 Tập 2: Trong mặt phẳng toạ độ Oxy, cho điểm M(– 1; 3).

a) Tìm toạ độ điểm A đối xứng với điểm M qua gốc O.

b) Tìm toạ độ điểm B đối xứng với điểm M qua trục Ox.

c) Tìm toạ độ điểm C đối xứng với điểm M qua trục Oy

Lời giải:

a) Điểm A đối xứng với điểm M qua gốc O nên O là trung điểm của AM.

Do đó $\overrightarrow{AO}=\overrightarrow{OM}$.

Gọi tọa độ điểm A(a; b).

Ta có: $\overrightarrow{AO}=\left(0-a;0-b\right)=\left(-a;-b\right)$; $\overrightarrow{OM}=\left(-1;3\right)$ (tọa độ vectơ $\overrightarrow{OM}$ chính là tọa độ điểm M).

Vậy tọa độ điểm A là A(1; – 3).

b) Vì điểm B đối xứng với điểm M qua trục Ox nên hoành độ của điểm B giữ nguyên và tung độ của điểm B đối nhau với trung độ của điểm M.

Vậy ta có tọa độ của B là B(– 1; – 3).

c) Điểm C đối xứng với điểm M qua trục Oy nên tung độ của điểm C giữ nguyên và hoành độ của điểm C đối nhau với hoành độ của điểm M.

Vậy tọa độ của điểm C là C(1; 3).

Bài 6 trang 66 Toán lớp 10 Tập 2: Trong mặt phẳng toạ độ Oxy, cho ba điểm không thẳng hàng A(– 3; 1), B(– 1; 3), I(4; 2). Tìm toạ độ của hai điểm C, D sao cho tứ giác ABCD là hình bình hành nhận I làm tâm đối xứng.

Lời giải:

Gọi tọa độ điểm C(x_C; y_C), tọa độ điểm D(x_D; y_D).

Khi đó ta có: $\overrightarrow{AI}=\left(4-\left(-3\right);2-1\right)=\left(7;1\right)$, $\overrightarrow{IC}=\left(x_C-4;y_C-2\right)$.

Vì I là tâm đối xứng của hình bình hành ABCD nên I là trung điểm của AC, do đó

Vậy tọa độ điểm C là C(11; 3).

Ta có: $\overrightarrow{AB}=\left(\left(-1\right)-\left(-3\right);3-1\right)=\left(2;2\right)$, $\overrightarrow{DC}=\left(11-x_D;3-y_D\right)$.

Vì ABCD là hình bình hành nên $\overrightarrow{AB}=\overrightarrow{DC}$$\iff \overrightarrow{DC}=\left(2;2\right)$

Vậy tọa độ điểm D là D(9; 1).

Bài 7 trang 66 Toán lớp 10 Tập 2: Trong mặt phẳng toạ độ Oxy, cho tam giác ABC. Các điểm M(1; – 2), N(4; – 1) và P(6; 2) lần lượt là trung điểm của các cạnh BC, CA, AB. Tìm tọa độ của các điểm A, B, C.

Lời giải:

Gọi tọa độ điểm A(x_A; y_A), B(x_B; y_B), C(x_C; y_C).

Xem thêm các bài giải SGK Toán 10 Cánh diều hay, chi tiết khác:

Bài tập cuối chương 6

Bài 1: Tọa độ của vectơ

Bài 2: Biểu thức tọa độ của các phép toán

Bài 3: Phương trình đường thẳng

Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

Lý thuyết Tọa độ của vectơ

I. Tọa độ của một điểm

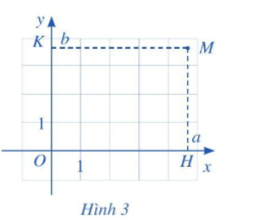
Để xác định tọa độ của một điểm M tùy ý trong mặt phẳng tọa độ Oxy, ta làm như sau (Hình 3):

+ Từ M kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm H ứng với số a. Số a là hoành độ của điểm M.

+ Từ M kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm K ứng với số b. Số b là tung độ của điểm M.

Cặp số (a; b) là tọa độ của điểm M trong mặt phẳng tọa độ Oxy. Ta kí hiệu là M(a ; b).

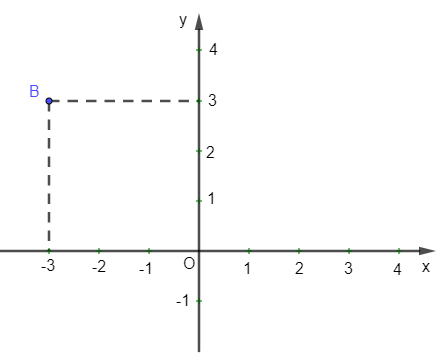
Ví dụ: Xác định tọa độ của điểm B trong hình vẽ sau:

Hướng dẫn giải

+ Từ B kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm ứng với số –3. Số –3 là hoành độ của điểm B.

+ Từ B kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm ứng với số 3. Số 3 là tung độ của điểm M.

Khi đó, cặp số (–3; 3) là tọa độ của điểm B.

Vậy điểm B có tọa độ là B(–3; 3).

II. Tọa độ của một vectơ

Tọa độ của điểm M được gọi là tọa độ của vectơ $\overrightarrow{OM}$.

Nếu $\overrightarrow{OM}$ có tọa độ (a; b) thì ta viết $\overrightarrow{OM}$ = (a; b) hay $\overrightarrow{OM}$ (a; b), trong đó a gọi là hoành độ của vectơ $\overrightarrow{OM}$ và b gọi là tung độ của vectơ $\overrightarrow{OM}$ (Hình 4).

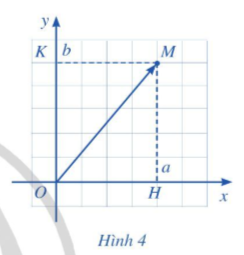
Chú ý: Trong mặt phẳng tọa độ Oxy, ta có:

+ $\overrightarrow{OM}$ = (a; b) ⇔ M(a ; b).

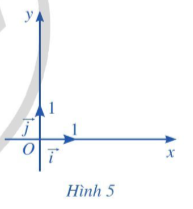
+ Vectơ $\overrightarrow{i}$ có điểm gốc là O và có tọa độ (1; 0) gọi là vectơ đơn vị trên trục Ox.

Vectơ $\overrightarrow{j}$ có điểm gốc là O và có tọa độ (0; 1) gọi là vectơ đơn vị trên trục Oy (Hình 4).

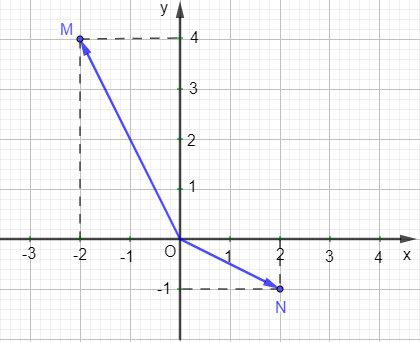
Ví dụ: Tìm tọa độ của vectơ $\overrightarrow{OM}$, $\overrightarrow{ON}$ trong hình sau:

Hướng dẫn giải

Ta thấy điểm M có tọa độ là (–2 ; 4)

Suy ra $\overrightarrow{OM}$ = (–2 ; 4).

Điểm N có tọa độ là (2 ; –1)

Suy ra $\overrightarrow{ON}$ = (2 ; –1).

Vậy $\overrightarrow{OM}$ = (–2 ; 4) và $\overrightarrow{ON}$ = (2 ; –1).

Nhận xét:

– Với mỗi vectơ $\overrightarrow{u}$, ta xác định được duy nhất một điểm A sao cho $\overrightarrow{OA}$ = $\overrightarrow{u}$.

– Với mỗi vectơ $\overrightarrow{u}$ trong mặt phẳng tọa độ Oxy, tọa độ của vectơ $\overrightarrow{u}$ là tọa độ của điểm A, trong đó A là điểm sao cho $\overrightarrow{OA}$ = $\overrightarrow{u}$.

– Nếu $\overrightarrow{u}$ có tọa độ (a; b) thì ta viết $\overrightarrow{u}$ = (a; b) hay $\overrightarrow{u}$(a; b), trong đó a gọi là hoành độ của vectơ $\overrightarrow{u}$ và b gọi là tung độ của vectơ $\overrightarrow{u}$.

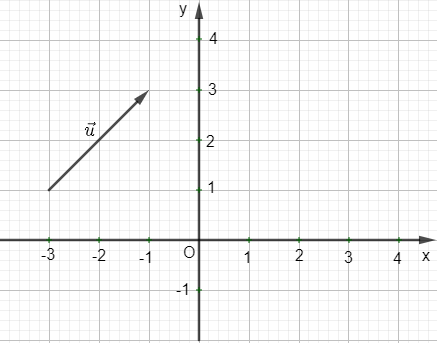
Ví dụ: Tìm tọa độ của vectơ $\overrightarrow{u}$ trong hình vẽ sau:

Hướng dẫn giải

Ta xác định vectơ $\overrightarrow{u}$ = $\overrightarrow{OA}$ như hình sau:

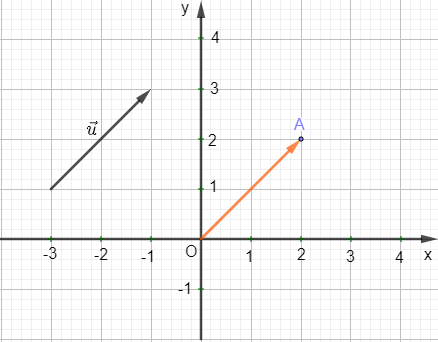
Ta thấy điểm A(2 ; 2) nên $\overrightarrow{OA}$ = (2 ; 2).

Suy ra $\overrightarrow{u}$ = (2 ; 2).

Vậy $\overrightarrow{u}$ = (2 ; 2).

Định lí: Trong mặt phẳng tọa độ Oxy, nếu $\overrightarrow{u}$ = (a ; b)  thì $\overrightarrow{u}$ = a$\overrightarrow{i}$ + b$\overrightarrow{j}$. Ngược lại, nếu $\overrightarrow{u}$ = a$\overrightarrow{i}$ + b$\overrightarrow{j}$ thì $\overrightarrow{u}$ = (a ; b).

Chú ý: Với $\overrightarrow{a}$ = (x₁ ; y₁) và $\overrightarrow{b}$ = (x₂ ; y₂), ta có $\overrightarrow{a}$ = $\overrightarrow{b}$ ⇔ $\left\{\begin{array}{l}{x}_1=x_2\\ y_1=y_2\end{array}\right.$ 

Như vậy, mỗi vectơ hoàn toàn được xác định khi biết tọa độ của nó.

Ví dụ: Trong mặt phẳng tọa độ Oxy, cho điểm M(2; 3) và vectơ $\overrightarrow{u}$ = (1; – 3).

a) Biểu diễn vectơ $\overrightarrow{u}$ qua hai vectơ $\overrightarrow{i}$ và $\overrightarrow{j}$.

b) Biểu diễn vectơ $\overrightarrow{OM}$  qua hai vectơ $\overrightarrow{i}$ và $\overrightarrow{j}$.

Hướng dẫn giải

a) Vì vectơ $\overrightarrow{u}$ = (1; – 3) nên $\overrightarrow{u}$ = 1$\overrightarrow{i}$ + (– 3)$\overrightarrow{j}$ = $\overrightarrow{i}$ – 3$\overrightarrow{j}$

Vậy $\overrightarrow{u}$ = $\overrightarrow{i}$ – 3$\overrightarrow{j}$

b) Vì điểm M có tọa độ là (2 ; 3) nên $\overrightarrow{OM}$ = (2 ; 3).

Do đó: $\overrightarrow{OM}$ = 2$\overrightarrow{i}$ + 3$\overrightarrow{j}$.

Vậy $\overrightarrow{OM}$ = 2$\overrightarrow{i}$ + 3$\overrightarrow{j}$.

III. Liên hệ giữa tọa độ của điểm và tọa độ của vectơ

Trong mặt phẳng tọa độ Oxy, cho hai điểm A(x_A; y_A) và B(x_B; y_B).

Ta có $\overrightarrow{AB}$  = (x_B – x_A ; y_B – y_A).

Ví dụ: Cho hai điểm A(2; –4) và B(1; 5). Hãy tìm tọa độ của vectơ $\overrightarrow{AB}$.

Hướng dẫn giải

Ta có $\overrightarrow{AB}$ = (1 – 2; 5 – (–4)) = (–1 ; 9).

Vậy $\overrightarrow{AB}$ = (–1 ; 9).