Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài tập cuối chương 6 chi tiết sách Toán 10 Tập 2 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài tập cuối chương 6

Giải Toán 10 trang 53 Tập 2

Bài 1 trang 53 Toán lớp 10 Tập 2: Cho mẫu số liệu:

a) Số trung bình cộng của mẫu số liệu trên là:

A. 5.

B. 5,5.

C. 6.

D. 6,5.

b) Trung vị của mẫu số liệu trên là:

A. 5.

B. 5,5.

C. 6.

D. 6,5.

c) Tứ phân vị của mẫu số liệu trên là:

A. Q1 = 4, Q2 = 5, Q3 = 9.

B. Q1 = 1, Q2 = 5,5, Q3 = 11.

C. Q1 = 1, Q2 = 5, Q3 = 11.

D. Q1 = 2, Q2 = 5, Q3 = 10.

d) Khoảng biến thiên của mẫu số liệu trên là:

A. 5.

B. 6.

C. 10.

D. 11.

e) Khoảng tứ phân vị của mẫu số liệu trên là:

A. 7.

B. 8.

C. 9.

D. 10.

g) Phương sai của mẫu số liệu trên là:

A. $\sqrt{\frac{96}{7}}$.

B. $\frac{96}{7}$.

C. 96.

D. $\sqrt{96}$.

h) Độ lệch chuẩn của mẫu số liệu trên là:

A. $\sqrt{\frac{96}{7}}$.

B. $\frac{96}{7}$.

C. 96.

D. $\sqrt{96}$.

Lời giải:

a) Đáp án đúng là: C.

Số trung bình cộng của mẫu số liệu đã cho là:

$\overline{x}=\frac{1+2+4+5+9+10+11}{7}=6$

b) Đáp án đúng là: A.

Mẫu số liệu đã được xếp theo thứ tự không giảm.

Cỡ mẫu là 7 nên trung vị mẫu là Me = 5.

c) Đáp án đúng là: D.

Tứ phân vị thứ hai là Q2 = Me = 5.

Tứ phân vị thứ nhất là trung vị của dãy 124 nên Q1 = 2.

Tứ phân vị thứ ba là trung vị của dãy 91011 nên Q3 = 10.

Vậy Q1 = 2, Q2 = 5, Q3 = 10.

d) Đáp án đúng là: C.

Khoảng biến thiên của mẫu số liệu là R = 11 – 1 = 10.

e) Đáp án đúng là: B.

Khoảng tứ phân vị của mẫu số liệu là ∆Q = Q3 – Q1 = 10 – 2 = 8.

g) Đáp án đúng là: B.

Phương sai của mẫu số liệu là:

s2 = $\frac{1}{7}$[(1 – 6)2 + (2 – 6)2 + (4 – 6)2 + (5 – 6)2 + (9 – 6)2 + (10 – 6)2 + (11 – 6)2]

= $\frac{96}{7}$.

h) Đáp án đúng là: A.

Độ lệch chuẩn của mẫu số liệu là s = $\sqrt{s^2}=\sqrt{\frac{96}{7}}$.

Bài 2 trang 53 Toán lớp 10 Tập 2: Bảng 6 thống kê số áo sơ mi nam bán được của một cửa hàng trong một tháng.

Mốt của mẫu số liệu trên là bao nhiêu?

A. 42.

B. 47.

C. 32.

D. 39.

Lời giải:

Đáp án đúng là: D.

Quan sát bảng tần số ta thấy cỡ áo 39 có tần số lớn nhất (47) nên mốt của mẫu số liệu là M_o = 39.

Bài 3 trang 53 Toán lớp 10 Tập 2: Biểu đồ đoạn thẳng ở Hình 6 cho biết lượng khách du lịch quốc tế đến Việt Nam trong một số năm (từ 1990 đến 2019).

a) Viết mẫu số liệu thống kê số lượt khách du lịch quốc tế đến Việt Nam nhận được từ biểu đồ bên.

b) Viết mẫu số liệu theo thứ tự tăng dần. Tìm số trung bình cộng, trung vị và tứ phân vị của mẫu số liệu đó.

c) Tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu đó.

d) Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.

Lời giải:

a) Mẫu số liệu thống kê số lượt khách du lịch quốc tế đến Việt Nam nhận được từ biểu đồ trên là:

b) Sắp xếp mẫu số liệu theo thứ tự tăng dần là:

Giải Toán 10 trang 54 Tập 2

Bài 4 trang 54 Toán lớp 10 Tập 2: Lớp 10A có 40 học sinh. Tỉ số phần trăm về phương tiện mà các bạn đến trường được mô tả như biểu đồ ở Hình 7.

a) Có bao nhiêu bạn đi xe đạp đến trường?

b) Chọn ngẫu nhiên một bạn để phân công vào đội xung kích của trường. Tính xác suất của biến cố “Bạn được chọn là bạn đến trường bằng xe đạp”.

Lời giải:

a) Quan sát biểu đồ Hình 7 ta thấy, số bạn đi xe đạp đến trường chiếm 40% tổng số bạn học sinh của lớp 10A.

Mà lớp 10A có 40 học sinh.

Nên số bạn đi xe đạp đến trường là: 40 . 40% = $40.\frac{40}{100}=16$(bạn).

Vậy có 16 bạn đi xe đạp đến trường.

b) Chọn 1 bạn trong 40 bạn của lớp để phân công vào đội xung kích, có 40 cách chọn hay số phần tử của không gian mẫu trong phép thử này là n(Ω) = 40.

Gọi biến cố A: “Bạn được chọn là bạn đến trường bằng xe đạp”.

Theo câu a, có 16 bạn đi xe đạp đến trường, ta chọn 1 bạn trong 16 bạn này, có 16 cách chọn hay n(A) = 16.

Vậy xác suất của biến cố A là $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{16}{40}=\frac{2}{5}$.

Bài 5 trang 54 Toán lớp 10 Tập 2: Em hãy tìm hiểu chiều cao của tất cả các bạn trong tổ và lập mẫu số liệu với kết quả tăng dần. Với mẫu số liệu đó, hãy tìm:

a) Số trung bình cộng, trung vị và tứ phân vị;

b) Khoảng biến thiên và khoảng tứ phân vị;

c) Phương sai và độ lệch chuẩn.

Lời giải:

Bài toán này sẽ có nhiều kết quả phụ thuộc vào chiều cao của các bạn trong tổ.

Bài 6 trang 54 Toán lớp 10 Tập 2: Trong một hội thảo quốc tế có 10 chuyên gia đến từ các nước ở châu Á, 12 chuyên gia đến từ các nước ở châu Âu. Chọn ngẫu nhiên 2 chuyên gia vào ban tổ chức. Xác suất của biến cố “Chọn được 2 chuyên gia ở hai châu lục khác nhau vào ban tổ chức” bằng bao nhiêu?

Lời giải:

Tổng số chuyên gia ở các nước châu Á và châu Âu là: 10 + 12 = 22 (chuyên gia).

Mỗi cách chọn ngẫu nhiên 2 chuyên gia vào ban tổ chức là một tổ hợp chập 2 của 22 phần tử. Do đó không gian mẫu Ω là số các tổ hợp chập 2 của 22 phần tử.

Khi đó n(Ω) = $C_{22}^2=231$.

Gọi biến cố A: “Chọn được 2 chuyên gia ở hai châu lục khác nhau vào ban tổ chức”.

Để chọn được 2 chuyên gia ở 2 châu lục khác nhau, ta chọn 1 chuyên gia ở châu Á và 1 chuyên gia ở châu Âu.

Chọn 1 chuyên gia ở châu Á trong 10 chuyên gia, có 10 cách chọn.

Chọn 1 chuyên gia ở châu Âu trong 12 chuyên gia, có 12 cách chọn.

Theo quy tắc nhân, số cách chọn 2 chuyên gia ở hai châu lục khác nhau là 10 . 12 = 120 cách chọn. Do đó n(A) = 120.

Vậy xác xuất của biến cố A là $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{120}{231}=\frac{40}{77}$.

Bài 7 trang 54 Toán lớp 10 Tập 2: Trong một buổi khiêu vũ có đúng 10 cặp vợ chồng. Chọn ngẫu nhiên 2 người lên khiêu vũ đầu tiên. Xác suất của biến cố “Chọn được 2 người là vợ chồng” bằng bao nhiêu?

Lời giải:

10 cặp vợ chồng thì có tất cả 20 người.

Mỗi cách chọn ngẫu nhiên 2 người lên khiêu vũ là một tổ hợp chập 2 của 20 phần tử. Do đó không gian mẫu Ω là số các tổ hợp chập 2 của 20 phần tử.

Khi đó n(Ω) = $C_{20}^2=190$.

Gọi biến cố A: “Chọn được 2 người là vợ chồng”.

Vì có đúng 10 cặp vợ chọn nên chọn được 2 người là vợ chồng thì có 10 cách chọn. Do đó n(A) = 10.

Vậy xác xuất của biến cố A là $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{10}{190}=\frac{1}{19}$.

Bài 8 trang 54 Toán lớp 10 Tập 2: Một lô hàng có 20 sản phẩm bao gồm 16 chính phẩm và 4 phế phẩm. Chọn ngẫu nhiên 3 sản phẩm.

a) Có bao nhiêu kết quả xảy ra khi chọn ngẫu nhiên 3 sản phẩm?

b) Xác suất của biến cố “Cả 3 sản phẩm được chọn là chính phẩm” bằng bao nhiêu?

Lời giải:

a) Mỗi cách chọn ngẫu nhiên 3 sản phẩm trong 20 sản phẩm là một tổ hợp chập 3 của 20 phần tử. Do đó số cách chọn ngẫu nhiên 3 sản phẩm là số các tổ hợp chập 2 của 20 phần tử và là $C_{20}^3=1140$.

Vậy có 1 140 kết quả xảy ra khi chọn ngẫu nhiên 3 sản phẩm.

b) Từ câu a ta có n(Ω) = 1 140.

Gọi biến cố A: “Cả 3 sản phẩm được chọn là chính phẩm”.

Chọn 3 sản phẩm là chính phẩm trong 16 chính phẩm, số cách chọn là $C_{16}^3=560$.

Do đó n(A) = 560.

Vậy xác xuất của biến cố A là $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{560}{1140}=\frac{28}{57}$.

Bài 9 trang 54 Toán lớp 10 Tập 2: Trong một hộp có 20 chiếc thẻ cùng loại được viết các số 1, 2, 3, ..., 20 sao cho mỗi thẻ chỉ viết một số và hai thẻ khác nhau viết hai số khác nhau. Chọn ngẫu nhiên 2 chiếc thẻ. Tính xác suất của biến cố “Hai thẻ được chọn có tích của hai số được viết trên đó là số lẻ”.

Lời giải:

Mỗi cách chọn ngẫu nhiên 2 thẻ trong 20 chiếc thẻ là một tổ hợp chập 2 của 20 phần tử. Do đó không gian mẫu Ω là số các tổ hợp chập 2 của 20 phần tử.

Vậy n(Ω) = $C_{20}^2=190$.

Gọi biến cố A: “Hai thẻ được chọn có tích của hai số được viết trên đó là số lẻ”.

Tích của hai số là số lẻ khi cả hai số đó đều là số lẻ.

Các số tự nhiên lẻ từ 1 đến 20 là: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19. Có 10 số.

Do đó có 10 chiếc thẻ ghi số lẻ.

Số cách chọn 2 thẻ ghi số lẻ trong 10 thẻ ghi số lẻ là $C_{10}^2=45$.

Khi đó n(A) = 45.

Vậy xác xuất của biến cố A là $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{45}{190}=\frac{9}{38}$.

Xem thêm các bài giải SGK Toán 10 Cánh diều hay, chi tiết khác:

Bài 5: Xác suất của biến cố

Bài tập cuối chương 6

Bài 1: Tọa độ của vectơ

Bài 2: Biểu thức tọa độ của các phép toán

Bài 3: Phương trình đường thẳng

Lý thuyết 

1. Số gần đúng

Trong đo đạc và tính toán, ta thường chỉ nhận được các số gần đúng.

Ví dụ: Dân số Việt Nam năm 2017 ước tính là 93,7 triệu người. Khi đó con số 93,7 triệu người là số gần đúng.

2. Sai số của số gần đúng

a. Sai số tuyệt đối

Nếu a là số gần đúng của số đúng $\overline{a}$ thì ∆_a = $\left|\overline{a}-a\right|$ được gọi là sai số tuyệt đối của số gần đúng a (Hình vẽ).

Chú ý: Sai số tuyệt đối của số gần đúng nhận được trong một phép đo đạc, tính toán càng bé thì kết quả của phép đo đạc, tính toán đó càng chính xác.

Ví dụ: Hai bạn Nam và Long muốn tính chu vi của một đường tròn có bán kính 1 cm. Bạn Nam lấy π là 3,14 còn Long lấy π là 3,1. Hỏi kết quả của bạn nào chính xác hơn.

Hướng dẫn giải

Gọi chu vi đường tròn bán kính r = 1 cm là C = 2πr (cm).

Bạn Nam tính được chu vi của đường tròn khi lấy π = 3,14 là:

C₁ = 2πr = 2.3,14.1 = 6,28 (cm).

Bạn Long tính được chu vi của đường tròn khi lấy π = 3,1 là:

C₂ = 2πr = 2.3,1.1 = 6,2 (cm).

Ta thấy 3,1 < 3,14 < π nên 2.3,1.1 < 2.3,14.1 < 2.π.1

Tức là C₂ < C₁ < C.

Suy ra ${\Delta }_{C_1}=\left|C-C_1\right|<\left|C-C_2\right|={\Delta }_{C_2}$.

⇒ ${\Delta }_{C_1}<{\Delta }_{C_2}$.

⇒ Kết quả của bạn Nam chính xác hơn kết quả của bạn Long.

Vậy kết quả tính chu vi đường tròn của bạn Nam chính xác hơn kết quả của bạn Long.

b. Độ chính xác của một số gần đúng

Nhận xét:

- Giả sử a là số gần đúng của số đúng $\overline{a}$ sao cho ∆_a = $\left|\overline{a}-a\right|$≤ d.

Khi đó ∆_a = $\left|\overline{a}-a\right|$ ≤ d ⇔ –d ≤ $\overline{a}-a$ ≤ d ⇔ a – d ≤ $\overline{a}$ ≤ a + d.

- Ta nói a là số gần đúng của số đúng $\overline{a}$ với độ chính xác d nếu ∆_a = $\left|\overline{a}-a\right|$ ≤ d và quy ước viết gọn là $\overline{a}$ = a ± d.

- Nếu ∆_a ≤ d thì số đúng $\overline{a}$ nằm trong đoạn [a – d; a + d]. Bởi vậy, d càng nhỏ thì độ sai lệch của số gần đúng a so với số đúng $\overline{a}$ càng ít. Điều đó giải thích vì sao d được gọi là độ chính xác của số gần đúng.

Ví dụ: Tính độ chính xác của kết quả phép tính chu vi đường tròn bán kính 1 cm khi lấy π là 3,14.

Hướng dẫn giải

Khi lấy π là 3,14 ta có chu vi đường tròn bán kính r = 1 cm là

C₁ = 2.3,14.1 = 6,28 (cm).

Vì 3,14 < π < 3,15 nên 2.3,14.1 < 2π.1 < 2.3,15.1

⇒ 6,28 < C < 6,3

${\Delta }_{C_1}$ = |C – 6,28| < 6,3 – 6,28 = 0,02.

Vậy độ chính xác của phép tính này là 0,02.

c. Sai số tương đối

Tỉ số δ_a = $\frac{{\Delta }_a}{\left|a\right|}$ được gọi là sai số tương đối của số gần đúng a.

Nhận xét:

- Nếu $\overline{a}$ = a ± d thì ∆_a ≤ d. Do đó δ_a ≤ $\frac{d}{\left|a\right|}$. Vì vậy, nếu $\frac{d}{\left|a\right|}$ càng bé thì chất lượng của phép đo đạc, tính toán càng cao.

- Người ta thường viết sai số tương đối dưới dạng phần trăm.

Chẳng hạn, trong phép đo thời gian Trái Đất quay một vòng quanh Mặt Trời thì sai số tương đối không vượt quá $\frac{\frac{1}{4}}{365}=\frac{1}{1\text{ 460}}\approx 0,068\%$ .

Ví dụ: Trong phép đo chiều dài của một đoạn đường thu được kết quả là 13,1 m với độ chính xác là 0,1 m. Hãy đánh giá sai số tương đối của số gần đúng này.

Hướng dẫn giải

Ta có số gần đúng a = 13,1 m và độ chính xác d = 0,1 m.

Do đó sai số tương đối là: ${\delta }_a\le \frac{d}{\left|a\right|}=\frac{0,1}{13,1}\approx 0,76\%$.

Vậy sai số tương đối không vượt quá 0,76%.

3. Số quy tròn. Quy tròn số đúng và số gần đúng

a. Số quy tròn

Khi quy tròn một số nguyên hoặc một số thập phân đến một hàng nào đó thì số nhận được gọi là số quy tròn của số ban đầu.

Ví dụ: Quy tròn số 5,123 đến hàng phần trăm ta được số 5,12. Khi đó số 5,12 được gọi là số quy tròn của số 5,123.

b. Quy tròn số đến một hàng cho trước

Nhận xét: Khi quy tròn số nguyên hoặc số thập phân đến một hàng cho trước thì sai số tuyệt đối của số quy tròn không vượt quá nửa đơn vị của hàng quy tròn. Như vậy, ta có thể lấy độ chính xác của số quy tròn bằng nửa đơn vị của hàng quy tròn.

Ví dụ: Quy tròn số 2,516 đến hàng phần trăm rồi ước lượng độ chính xác của số đó.

Hướng dẫn giải

Quy tròn số 2,516 đến hàng phần trăm ta được số 2,52.

Sai số tuyệt đối là |2,516 – 2,52| = 0,004 < 0,005.

Vậy số quy tròn 2,52 là số gần đúng của 2,516 với độ chính xác 0,005.

c. Quy tròn số gần đúng căn cứ vào độ chính xác cho trước

Quy ước: Cho a là số gần đúng với độ chính xác d. Giả sử a là số nguyên hoặc số thập phân. Khi được yêu cầu quy tròn số a mà không nói rõ quy tròn đến hàng nào thì ta quy tròn a đến hàng thấp nhất mà d nhỏ hơn một đơn vị của hàng đó.

Ví dụ: Viết số quy tròn của số 1 348 với d = 300.

Hướng dẫn giải

Vì độ chính xác d = 300 thỏa mãn 100 < d = 300 < 1 000 nên hàng thấp nhất mà d nhỏ hơn một đơn vị của hàng đó là hàng nghìn.

Vì vậy, ta quy tròn số 1 348 đến hàng nghìn.

Quy tròn số 1 348 đến hàng nghìn ta được số 1 000.

Vậy số quy tròn của số 1 348 với độ chính xác d = 300 là 1 000.

4. Số trung bình cộng (Số trung bình)

a. Định nghĩa

Số trung bình cộng của một mẫu n số liệu thống kê bằng tổng của các số liệu chia cho số các số liệu đó. Số trung bình cộng $\overline{x}$ của mẫu số liệu x₁, x₂, …, x_n là:

$\overline{x}=\frac{x_1+x_2+\mathrm{...}+x_n}{n}$ .

Ví dụ: Tìm số trung bình cộng của các số 13, 15, 17, 20.

Hướng dẫn giải

Mẫu trên có 4 số liệu.

Khi đó, số trung bình cộng là $\overline{x}=\frac{13+15+17+20}{4}=16,25$.

Vậy trung bình cộng của các số đã cho là 16,25.

Nhận xét:

- Đối với bảng tần số:

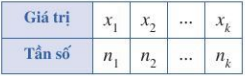
Số trung bình cộng $\overline{x}$ của mẫu số liệu thống kê trong bảng phân bố tần số là:

 $\overline{x}=\frac{n_1{x}_1+n_2{x}_2+\mathrm{...}+n_k{x}_k}{n_1+n_2+\mathrm{...}+n_k}$

- Đối với bảng tần số tương đối:

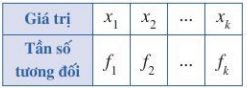
Số trung bình cộng $\overline{x}$ của mẫu số liệu thống kê trong bảng phân bố tần số tương đối là: $\overline{x}=f_1{x}_1+f_2{x}_2+\mathrm{...}+f_k{x}_k,$

trong đó $f_1=\frac{n_1}{n}$ , $f_2=\frac{n_2}{n}$, …, $f_k=\frac{n_k}{n}$, với n = n₁ + n₂ + …+ n_k.

Ví dụ:

a) Thời gian giải một bài toán (đơn vị: phút) của 30 học sinh được ghi lại trong bảng tần số sau:

Tính thời gian trung bình để giải bài toán trên.

b) Số cân nặng (đơn vị: kg) của 20 học sinh được ghi lại trong bảng tần số tương đối sau:

Hãy tính cân nặng trung bình của 20 học sinh.

Hướng dẫn giải

a) Thời gian trung bình để giải bài toán trên là

$\overline{x}=\frac{5.5+4.6+2.7+3.8+4.9+1.10+3.12+5.13+3.15}{5+4+2+3+4+1+3+5+3}=9,3$.

Vậy thời gian trung bình để giải bài toán trên là 9,3 phút.

b) Ta có cân nặng trung bình của 20 học sinh là:

$\overline{x}=\frac{1}{10}.28+\frac{3}{20}.29+\frac{1}{5}.30+\frac{3}{10}.35+\frac{1}{5}.37+\frac{1}{20}.42=33,15$.

Vậy cân nặng trung bình của 20 học sinh là 33,15 kg.

b. Ý nghĩa

Khi các số liệu trong mẫu ít sai lệch với số trung bình cộng, ta có thể giải quyết được vấn đề trên bằng cách lấy số trung bình cộng làm đại diện cho mẫu số liệu.

Ví dụ: Để dự báo lượng mưa trong tháng 8 tại Hà Nội người ta tiến hành đo lượng mưa của từng ngày của tháng 8 gồm 31 số liệu. Số trung bình cộng của mẫu số liệu đó được xem như lượng mưa trung bình tháng 8 tại Hà Nội. Thống kê lượng mưa trung bình tháng 8 tại Hà Nội trong nhiều năm liên tiếp sẽ cho ta những dự báo lượng mưa trung bình tháng 8 tại Hà Nội trong những năm sắp tới.

5. Trung vị

a. Định nghĩa

Sắp thứ tự mẫu số liệu gồm n số liệu thành một dãy không giảm (hoặc không tăng).

- Nếu n là số lẻ thì số liệu đứng ở vị trí thứ $\frac{n+1}{2}$ (số đứng chính giữa) gọi là trung vị.

- Nếu n là số chẵn thì số trung bình cộng của hai số liệu đứng ở vị trí thứ $\frac{n}{2}$ và  $\frac{n}{2}+1$ gọi là trung vị.

Trung vị kí hiệu là M_e.

Nhận xét:

- Trung vị không nhất thiết là một số trong mẫu số liệu và dễ tính toán.

- Khi các số liệu trong mẫu không có sự chênh lệch lớn thì số trung bình cộng và trung vị xấp xỉ nhau.

Ví dụ: Điểm kiểm tra Toán của 7 bạn học sinh tổ 1 lớp 10B như sau: 9; 5; 4; 5; 8; 7; 9. Tìm trung vị M_e của mẫu số liệu trên.

Hướng dẫn giải

 - Sắp xếp số liệu của mẫu theo thứ tự không giảm:

4        5        5        7        8        9        9

- Xác định xem số các số liệu là chẵn hay lẻ để tìm số trung vị:

Mẫu có 7 số liệu. Giá trị chính giữa là 7. Vì thế, trung vị của mẫu là 7.

Vậy M_e = 7.

b. Ý nghĩa

Nếu những số liệu trong mẫu có sự chênh lệch lớn thì ta nên chọn thêm trung vị làm đại diện cho mẫu số liệu đó nhằm điều chỉnh một số hạn chế khi sử dụng số trung bình cộng. Những kết luận về đối tượng thống kê rút ra khi đó sẽ tin cậy hơn.

Ví dụ: Thời gian giải một bài tập (đơn vị: phút) của nhóm học sinh như sau:

20      3        2        5        6        1

Tính trung vị của mẫu và số trung bình cộng của mẫu.

Ta nên chọn trung vị hay số trung bình cộng để đại diện cho mẫu thì kết luận về thời gian giải một bài tập của nhóm học sinh sẽ đáng tin cậy hơn?

Hướng dẫn giải

Sắp xếp các số liệu theo thứ tự không giảm:

1        2        3        5        6        20

Mẫu có 6 số liệu, khi đó trung vị của mẫu là trung bình cộng của 3 và 5.

Ta có M_e = $\frac{3+5}{2}=4$.

Trung bình cộng của mẫu số liệu: $\overline{x}=\frac{1+2+3+5+6+20}{6}\approx 6,2$.

Ta thấy nên lựa chọn trung vị M_e = 4 đại diện cho mẫu thì kết luận thời gian giải một bài tập của nhóm học sinh sẽ đáng tin cậy hơn.

Vậy trung vị của mẫu là M_e = 4; số trung bình cộng là 6,2 và nên lựa chọn trung vị M_e = 4 đại diện cho mẫu thì kết luận thời gian giải một bài tập của nhóm học sinh sẽ đáng tin cậy hơn.

6. Tứ phân vị

a. Định nghĩa

Sắp thứ tự mẫu số liệu gồm n số liệu thành một dãy không giảm.

Tứ phân vị của mẫu số liệu trên là bộ ba giá trị: tứ phân vị thứ nhất, tứ phân vị thứ hai và tứ phân vị thứ ba; ba giá trị này chia mẫu số liệu thành bốn phần có số lượng phần tử bằng nhau.

- Tứ phân vị thứ hai Q₂ bằng trung vị.

- Nếu n là số chẵn thì tứ phân vị thứ nhất Q₁ bằng trung vị của nửa dãy phía dưới và tứ phân vị thứ ba Q₃ bằng trung vị của nửa dãy phía trên.

- Nếu n là số lẻ thì tứ phân vị thứ nhất Q₁ bằng trung vị của nửa dãy phía dưới (không bao gồm Q₂) và tứ phân vị thứ ba Q₃ bằng trung vị của nửa dãy phía trên (không bao gồm Q₂).

Ta minh họa tứ phân vị của mẫu số liệu gồm 11 số liệu trên trục số như sau:

Ví dụ: Tìm tứ phân vị của mẫu số liệu sau:

21      32      10      45      11      35      24      8

Hướng dẫn giải

Mẫu số liệu trên được sắp xếp theo thứ tự tăng dần như sau:

8        10      11      21      24      32      35      45

Dãy số liệu trên gồm 8 số liệu, là số chẵn.

Do đó ta có:

• Trung vị của mẫu số liệu trên là: Q₂ = $\frac{21+24}{2}=22,5$.

• Trung vị của dãy 8, 10, 11, 21 là  Q₁ = $\frac{10+11}{2}=10,5$.

• Trung vị của dãy 24, 32, 35, 45 là  Q₃ = $\frac{32+35}{2}=33,5$.

Vậy Q₁ = 10,5, Q₂ = 22,5, Q₃ = 33,5.

Tứ phân vị đó được biểu diễn trên trục số như sau:

b. Ý nghĩa

- Trong thực tiễn, có những mẫu số liệu mà nhiều số liệu trong mẫu đó vẫn còn sự chênh lệch lớn so với trung vị. Ta nên chọn thêm những số khác cùng làm đại diện cho mẫu đó. Bằng cách lấy thêm trung vị của từng dãy số liệu tách ra bởi trung vị của mẫu nói trên, ta nhận được tứ phân vị đại diện cho mẫu số liệu đó.

- Bộ ba giá trị Q₁, Q₂, Q₃ trong tứ phân vị phản ánh độ phân tán của mẫu số liệu. Nhưng mỗi giá trị Q₁, Q₂, Q₃ lại đo xu thế trung tâm của phần số liệu tương ứng của mẫu đó.

7. Mốt

a. Định nghĩa

Mốt của mẫu số liệu là giá trị có tần số lớn nhất trong bảng phân bố tần số và kí hiệu là M_o.

Chú ý: Một mẫu số liệu có thể có nhiều mốt.

Ví dụ: Cho bảng tần số sau:

Tìm mốt của mẫu số liệu trên.

Hướng dẫn giải

Quan sát bảng tần số ta thấy giá trị 4 và 5 có tần số lớn nhất bằng 25.

Suy ra mốt của dấu hiệu là M_o = 4 và M_o = 5.

Vậy mốt của dấu hiệu là M_o = 4 và M_o = 5.

b. Ý nghĩa

Mốt của một mẫu số liệu đặc trưng cho số lần lặp đi lặp lạ nhiều nhất tại một vị trí của mẫu số liệu đó. Dựa vào mốt, ta có thể đưa ra những kết luận (có ích) về đối tượng thống kê.

Ví dụ: Một cửa hàng bán 5 loại quạt với giá tiền là 150; 200; 350; 400; 500 (nghìn đồng). Số quạt bán ra trong mùa hè vừa qua được thống kê trong bảng sau:

Năm nay cửa hàng nên nhập nhiều số lượng loại quạt có giá tiền bao nhiêu để bán?

Hướng dẫn giải

Quan sát bảng thống kê trên ta thấy quạt có giá 400 nghìn đồng có số lượng bán được nhiều nhất, nghĩa là quạt giá 400 nghìn có tần số lớn nhất.

Suy ra M_o = 400.

Vậy năm nay của hàng nên nhập nhiều quạt có giá tiền 400 nghìn đồng về để bán.

8. Tính hợp lí của số liệu thống kê

Sau khi thu thập, tổ chức, phân loại và biểu diễn số liệu bằng bảng hoặc biểu đồ, ta cần phân tích và xử lí các số liệu đó để xem xét tính hợp lí của số liệu thống kê, đặc biệt chỉ ra được những số liệu bất thường (hay còn gọi là dị biệt, trong tiếng Anh là Outliers). Ta có thể sử dụng các số liệu đặc trưng đo xu thế trung tâm cho mẫu số liệu không ghép nhóm để thực hiện điều đó.

Ví dụ: Chiều cao của một nhóm học sinh nữ 6 tuổi (đơn vị cm) được ghi lại như sau:

a) Tìm tứ phân vị của mẫu trên.

b) Từ kết quả câu a) bước đầu xác định những giá trị bất thường của mẫu số liệu trên.

Hướng dẫn giải

a) Ta sắp xếp các số liệu theo thứ tự tăng dần như sau:

Mẫu trên có 15 số liệu.

Trung vị của mẫu số liệu trên là Q₂ = 117.

Trung vị nửa phía dưới 97, 100, 112, 113, 115, 115, 116 là Q₁ = 113.

Trung vị nửa phía trên 118, 120, 122, 122, 123, 125, 145 là Q₃ = 122.

Vậy tứ phân vị của mẫu là Q₁ = 113; Q₂ = 117; Q₃ = 122.

b) Dựa vào trung vị và tứ phân vị của mẫu số liệu, bước đầu ta thấy những số liệu bất thường trong mẫu là 97 và 145.

9. Khoảng biến thiên. Khoảng tứ phân vị

a. Định nghĩa

- Trong một mẫu số liệu, khoảng biến thiên là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó.

Ta có thể tính khoảng biến thiên R của mẫu số liệu theo công thức sau: R = x_max – x_min, trong đó x_max là giá trị lớn nhất, x_min là giá trị nhỏ nhất của mẫu số liệu đó.

- Giả sử Q₁, Q₂, Q₃ là tứ phân vị của mẫu số liệu. Ta gọi hiệu ∆_Q = Q₃ – Q₁ là khoảng tứ phân vị của mẫu số liệu đó.

Chú ý: Khoảng tứ phân vị của mẫu số liệu còn gọi là khoảng trải giữa (tiếng Anh là InterQuartile Range – IQR) của mẫu số liệu đó.

Ví dụ: Mẫu số liệu thống kê cân nặng (đơn vị: kg) của 8 học sinh trong một tổ như sau:

45      52      41      37      50      52      66      49

a) Tìm khoảng biến thiên của mẫu số liệu trên.

b) Tìm khoảng tứ phân vị của mẫu số liệu trên.

Hướng dẫn giải

a) Trong mẫu có số liệu lớn nhất là 66, số liệu nhỏ nhất là 37.

Khi đó, khoảng biến thiên của mẫu là R = x_max­ – x_min = 66 – 37 = 29 (kg).

Vậy khoảng biến thiên của mẫu là R = 29 kg.

b) Sắp xếp mẫu theo thứ tự tăng dần, ta được:

37      41      45      49      50      52      52      66

Khi đó, trung vị của mẫu là: Q₂ = $\frac{49+50}{2}=49,5$.

Q₁ là trung vị của mẫu 37, 41, 45, 49 nên Q₁ = $\frac{41+45}{2}=43$.

Q₃ là trung vị của mẫu 50, 52, 52, 66 nên Q₃ = $\frac{52+52}{2}=52$.

Khi đó, ta có khoảng tứ phân vị là:

∆_Q = Q₃ – Q₁ = 52 – 43 = 9 (kg).

Vậy khoảng tứ phân vị của mẫu là ∆_Q = 9 kg.

b. Ý nghĩa

- Ý nghĩa của khoảng biến thiên: Khoảng biến thiên của mẫu số liệu phản ánh sự “dao động”, “sự dàn trải” của các số liệu trong mẫu đó. Khoảng biến thiên được sử dụng trong nhiều tình huống thực tiễn, chẳng hạn: tìm ra sự phân tán điểm kiểm tra của một lớp học hay xác định phạm vi giá cả của một dịch vụ …

Theo cách nhìn như ở trong vật lí, ở đó biên độ dao động phản ánh khoảng cách từ điểm cân bằng đến điểm xa nhất của dao động, nếu coi số trung bình cộng là “điểm cân bằng” của mẫu số liệu thì khoảng biến thiên của mẫu số liệu có thể xem như hai lần biên độ dao động của các số liệu trong mẫu đó quanh điểm cân bằng.

Trong các đại lượng đo mức độ phân tán của mẫu số liệu, khoảng biến thiên là đại lượng dễ hiểu, dễ tính toán và tương đối tốt đối với các mẫu số liệu nhỏ. Tuy nhiên, do khoảng biến thiên chỉ sử dụng hai giá trị x_max và x_min của mẫu số liệu nên đại lượng đó chưa diễn giải đầy đủ sự phân tán của số liệu trong mẫu. Ngoài ra, giá trị của khoảng biến thiên sẽ bị ảnh hưởng bởi các giá trị bất thường của mẫu số liệu đó. Trong những trường hợp như vậy, khoảng biến thiên của mẫu số liệu không phản ánh chính xác độ dàn trải của mẫu số liệu.

- Ý nghĩa của khoảng tứ phân vị: Khoảng tứ phân vị là đại lượng cho biết mức độ phân tán của 50% số liệu chính giữa của mẫu số liệu đã sắp xếp và có thể giúp xác định các giá trị bất thường của mẫu số liệu đó. Khoảng tứ phân vị thường được sử dụng thay cho khoảng biến thiên vì nó loại trừ hầu hết giá trị bất thường của mấu số liệu.

10. Phương sai

a. Định nghĩa

- Mỗi hiệu số giữa số liệu và số trung bình cộng gọi là độ lệch của số liệu đó đối với số trung bình cộng.

- Cho mẫu số liệu thống kê có n giá trị x₁, x₂, …, x_n và số trung bình cộng là $\overline{x}$.

Ta gọi số  $s^2=\frac{{\left(x_1-\overline{x}\right)}^2+{\left(x_2-\overline{x}\right)}^2+\mathrm{...}+{\left(x_n-\overline{x}\right)}^2}{n}$ là phương sai của mẫu số liệu trên.

Nhận xét:

- Khi có các số liệu bằng nhau, ta có thể tính phương sai theo công thức sau:

+ Đối với bảng tần số:

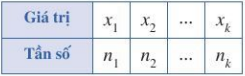
Phương sai của mẫu số liệu thống kê trong bảng phân bố tần số là:

$s^2=\frac{n_1{\left(x_1-\overline{x}\right)}^2+n_2{\left(x_2-\overline{x}\right)}^2+\mathrm{...}+n_k{\left(x_k-\overline{x}\right)}^2}{n},$

trong đó n = n₁ + n₂ + …+ n_k ; $\overline{x}$ là số trung bình cộng của các số liệu đã cho.

+ Đối với bảng phân bố tần số tương đối:

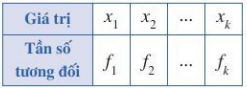
Phương sai của mẫu số liệu thống kê trong bảng phân bố tần số tương đối là:

$s^2=f_1{\left(x_1-\overline{x}\right)}^2+f_2{\left(x_2-\overline{x}\right)}^2+\mathrm{...}+f_k{\left(x_k-\overline{x}\right)}^2,$

trong đó $\overline{x}$ là số trung bình cộng của số liệu đã cho.

- Trong thực tế, người ta còn dùng công thức sau để tính phương sai của mẫu số liệu:

${\widehat{s}}^2=\frac{{\left(x_1-\overline{x}\right)}^2+{\left(x_2-\overline{x}\right)}^2+\mathrm{...}+{\left(x_n-\overline{x}\right)}^2}{n-1},$

trong đó: x_i là giá trị của quan sát thứ i; $\overline{x}$ là giá trị trung bình và n là số quan sát trong mẫu số liệu đó.

Ví dụ: Hai lớp 10A và 10B của một trường THPT đồng thời làm bài thi môn Toán theo cùng một đề thi. Kết quả được ghi lại trong bảng tần số sau:

Điểm thi của lớp 10A:

Điểm thi của lớp 10B:

a) Tính phương sai của từng mẫu số liệu ở hai bảng trên.

b) Xét xem kết quả bài thi của lớp nào đồng đều hơn.

Hướng dẫn giải

Ta có điểm thi trung bình của lớp 10A là:

${\overline{x}}_{10A}=\frac{3.5+7.6+12.7+14.8+3.9+1.10}{3+7+12+14+3+1}=7,25$

Điểm thi trung bình của lớp 10A là:

${\overline{x}}_{10B}=\frac{8.6+18.7+10.8+4.9}{8+18+10+4}=7,25$

Ta có phương sai của mẫu số liệu lớp 10A là:

$s_{10A}^2=\frac{3{\left(5-7,25\right)}^2+7{\left(6-7,25\right)}^2+\mathrm{...}+1.{\left(10-7,25\right)}^2}{3+7+12+14+3+1}=1,2875$

⇒ $s_{10A}^2$ = 1,2875

Ta có phương sai của mẫu số liệu lớp 10B là:

$s_{10B}^2=\frac{8{\left(6-7,25\right)}^2+18{\left(7-7,25\right)}^2+10.{\left(8-7,25\right)}^2+4.{\left(9-7,25\right)}^2}{8+18+10+4}=0,7875$

⇒ $s_{10B}^2$ = 0,7875.

Ta thấy điểm thi trung bình của lớp 10A và 10B bằng nhau đều bằng 7,25. Nhưng phương sai bảng điểm của lớp 10A lại lớn hơn phương sai bảng điểm lớp 10B nên kết quả làm bài thi của lớp 10B đồng đều hơn lớp 10A.

b. Ý nghĩa

Phương sai là số đặc trưng đo mức độ phân tán của mẫu số liệu. Mẫu số liệu nào có phương sai nhỏ hơn thì mức độ phân tán (so với số trung bình cộng) của các số liệu trong mẫu đó sẽ thấp hơn.

11. Độ lệch chuẩn

a. Định nghĩa 

Căn bậc hai (số học) của phương sai gọi là độ lệch chuẩn của mẫu số liệu thống kê.

Nhận xét: Vì độ lệch chuẩn có cùng đơn vị đo với số liệu thống kê nên khi cần chú ý đến đơn vị đo thì ta sử dụng độ lệch chuẩn mà không sử dụng phương sai.

Ví dụ: Cho mẫu số liệu:

23      22      20      12      35

Tính độ lệch chuẩn của mẫu trên.

Hướng dẫn giải

Mẫu trên có 5 số liệu.

Số trung bình của mẫu trên là: $\overline{x}=\frac{23+22+20+12+35}{5}=22,4$.

Phương sai của mẫu số liệu đó là:

$s^2=\frac{{\left(23-22,4\right)}^2+{\left(22-22,4\right)}^2+{\left(20-22,4\right)}^2+{\left(12-22,4\right)}^2+{(35-22,4)}^2}{5}=54,64$

⇒ s = $\sqrt{s^2}$ = $\sqrt{54,64}$ ≈ 7,39.

Vậy độ lệch chuẩn của mẫu là 7,39.

b. Ý nghĩa

Cũng như phương sai, khi hai mấu số liệu thống kê có cùng đơn vị đo và có số trung bình cộng bằng nhau (hoặc xấp xỉ nhau), mẫu số liệu nào có độ lệch chuẩn nhỏ hơn thì mức độ phân tán (so với số trung bình cộng) của các số liệu trong mẫu đó sẽ thấp hơn. Độ lệch chuẩn là số đặc trưng đo mức độ phân tán của mẫu số liệu thống kê có cùng đơn vị đo.

12. Giá trị bất thường của số liệu thống kê

Ta có thể sử dụng các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm để chỉ ra được những số liệu bất thường của mẫu số liệu đó. Ta thường sử dụng khoảng tứ phân vị để xác định số liệu bất thường của mẫu số liệu. Cụ thể như sau:

Giả sử Q₁, Q₂, Q₃ là tứ phân vị của mẫu số liệu và hiệu ∆_Q = Q₃ – Q₁ là khoảng tứ phân vị của mẫu số liệu đó. Một giá trị trong mẫu số liệu được coi là một giá trị bất thường nếu nó nhỏ hơn $Q_1-\frac{3}{2}{\Delta }_Q$ hoặc lớn hơn $Q_3+\frac{3}{2}{\Delta }_Q$. Như vậy, khoảng tứ phân vị cho ta cách nhận biết giá trị bất thường của mẫu số liệu.

Chú ý: Ta cũng có thể xác định số liệu bất thường của mẫu số liệu bằng số trung bình cộng và độ lệch chuẩn. Cụ thể như sau:

Giả sử $\overline{x}$, s lần lượt là số trung bình cộng và độ lệch chuẩn của mẫu số liệu. Một giá trị trong mẫu số liệu cũng được coi là một giá trị bất thường nếu nó nhỏ hơn $\overline{x}$ – 3s hoặc lớn hơn $\overline{x}$ + 3s. Như vậy, số trung bình cộng và độ lệch chuẩn cho ta cách nhận ra giá trị bất thường của mẫu số liệu.

Ví dụ: Hãy tìm các giá trị bất thường của mẫu số liệu sau:

12      4        10      –5      6        7        9        30

Hướng dẫn giải

Mẫu được sắp xếp theo thứ tự tăng dần là:

–5      4        6        7        9        10      12      30

Mẫu có 8 số liệu

Trung vị của mẫu là: $\frac{7+9}{2}$ = 8. Suy ra Q₂ = 8.

Trung vị nửa dưới –5, 4, 6, 7 là $\frac{4+6}{2}$ = 5. Suy ra Q₁ = 5.

Trung vị nửa trên 9, 10, 12, 30 là $\frac{10+12}{2}$ = 11. Suy ra Q₃ = 11.

Khoảng tứ phân vị là ∆_Q = Q₃ – Q₁ = 11 – 5 = 6.

Ta có: $Q_1-\frac{3}{2}{\Delta }_Q=5-\frac{3}{2}.6=-4$; $Q_3+\frac{3}{2}{\Delta }_Q=11+\frac{3}{2}.6=20$.

Ta thấy –5 < –4 và 30 > 20 nên các giá trị –5 và 30 là các giá trị bất thường của mẫu.

Vậy mẫu có hai giá trị bất thường là –5 và 30.

13. Xác suất của biến cố trong trò chơi tung đồng xu

- Trong trò chơi tung đồng xu, ta quy ước đồng xu là cân đối và đồng chất.

Nhận xét:

Khi tung một đồng xu hai lần liên tiếp:

+ Tập hợp Ω các kết quả có thể xảy ra đối với mặt xuất hiện của đồng xu sau hai lần tung là Ω = {SS; SN; NS; NN}, trong đó, chẳng hạn SN là kết quả “Lần thứ nhất đồng xu xuất hiện mặt sấp, lần thứ hai đồng xu xuất hiện mặt ngửa”.

+ Tập hợp Ω gọi là không gian mẫu trong trò chơi tung một đồng xu hai lần liên tiếp.

- Trong trò chơi tung một đồng xu hai lần liên tiếp, đối với mỗi biến cố A ta có định nghĩa cổ điển của xác suất như sau:

Xác suất của biến cố A, kí hiệu P(A), là tỉ số giữa số các kết quả thuận lợi cho biến cố A và số phần tử của không gian mẫu Ω:

P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)},$

ở đó n(A), n(Ω) lần lượt là số phần tử của hai tập hợp A và Ω.

Ví dụ: Tung một đồng xu hai lần liên tiếp.

a) Viết tập hợp Ω là không gian mẫu của trò chơi trên.

b) Xét biến cố A: “Có một lần đồng xu xuất hiện mặt sấp”. Tính xác suất của biến cố A.

Hướng dẫn giải

a) Không gian mẫu của trò chơi trên là: Ω = {SS; SN; NS; NN}.

Vậy không gian mẫu là Ω = {SS; SN; NS; NN}.

b) Từ Ω = {SS; SN; NS; NN} ⇒ n(Ω) = 4.

Có hai kết quả thuận lợi cho biến cố A là SN, NS, tức là A = {SN; NS} ⇒ n(A) = 2.

⇒ Xác suất của biến cố A là P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$= $\frac{2}{4}$ = $\frac{1}{2}$.

Vậy xác suất của biến cố A bằng $\frac{1}{2}$.

14. Xác suất của biến cố trong trò chơi gieo xúc xắc

- Trong trò chơi gieo xúc xắc, ta quy ước xúc xắc là cân đối và đồng chất.

Nhận xét: Khi gieo một xúc xắc hai lần liên tiếp, có 36 kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc sau hai lần gieo, đó là:

(1; 1)            (1; 2)          (1; 3)           (1; 4)           (1; 5)            (1; 6)

(2; 1)           (2; 2)           (2; 3)           (2; 4)           (2; 5)            (2; 6)

(3; 1)           (3; 2)           (3; 3)           (3; 4)           (3; 5)            (3; 6)

(4; 1)           (4; 2)           (4; 3)           (4; 4)           (4; 5)            (4; 6)

(5; 1)           (5; 2)           (5; 3)           (5; 4)           (5; 5)            (5; 6)

(6; 1)           (6; 2)           (6; 3)            (6; 4)          (6; 5)            (6; 6)

+ Tập hợp Ω các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc sau hai lần gieo là Ω = {(i; j)| i, j = 1, 2, 3, 4, 5, 6}, trong đó (i; j) là kết quả “Lần đầu xuất hiện mặt i chấm, lần sau xuất hiện mặt j chấm”.

+ Tập hợp Ω gọi là không gian mẫu trong trò chơi gieo một xúc xắc hai lần liên tiếp.

- Trong trò chơi gieo một xúc xắc hai lần liên tiếp, đối với mỗi biến cố C ta có định nghĩa cổ điển của xác suất như sau:

Xác suất của biến cố C, kí hiệu P(C), là tỉ số giữa số các kết quả thuận lợi cho biến cố C và số phần tử của không gian mẫu Ω:

P(C) = $\frac{n\left(C\right)}{n\left(\Omega \right)},$

ở đó n(C), n(Ω) lần lượt là số phần tử của hai tập hợp C và Ω.

Ví dụ: Gieo một con xúc xắc hai lần liên tiếp.

a) Viết tập hợp Ω là không gian mẫu của trò chơi trên.

b) Xét biến cố C: “Hai lần gieo xuất hiện ít nhất một mặt là số chẵn”. Tính xác suất của biến cố C.

Hướng dẫn giải

Không gian mẫu của trò chơi gieo một con xúc xắc hai lần là: Ω = {(i; j)| i, j = 1, 2, 3, 4, 5, 6}, trong đó (i; j) là kết quả “Lần đầu xuất hiện mặt i chấm, lần sau xuất hiện mặt j chấm”.

Vậy ta có không gian mẫu của trò chơi gieo một con xúc xắc hai lần là:

Ω = {(1; 1); (1; 2); (1; 3); (1; 4); (1; 5); (1; 6); (2; 1); (2; 2); (2; 3); (2; 4); (2; 5); (2; 6); (3; 1); (3; 2); (3; 3); (3; 4); (3; 5); (3; 6); (4; 1); (4; 2); (4; 3); (4; 4); (4; 5); (4; 6); (5; 1); (5; 2); (5; 3); (5; 4); (5; 5); (5; 6); (6; 1); (6; 2); (6; 3); (6; 4); (6; 5); (6; 6)}.

b) Từ Ω = {(1; 1); (1; 2); (1; 3); (1; 4); (1; 5); (1; 6); (2; 1); (2; 2); (2; 3); (2; 4); (2; 5); (2; 6); (3; 1); (3; 2); (3; 3); (3; 4); (3; 5); (3; 6); (4; 1); (4; 2); (4; 3); (4; 4); (4; 5); (4; 6); (5; 1); (5; 2); (5; 3); (5; 4); (5; 5); (5; 6); (6; 1); (6; 2); (6; 3); (6; 4); (6; 5); (6; 6)}.

⇒ n(Ω) = 36.

Các kết quả thuận lợi cho biến cố C là: (1; 2); (1; 4); (1; 6); (2; 1); (2; 2); (2; 3); (2; 4); (2; 5); (2; 6); (3; 2); (3; 4); (3; 6); (4; 1); (4; 2); (4; 3); (4; 4); (4; 5); (4; 6); (5; 2); (5; 4); (5; 6); (6; 1); (6; 2); (6; 3); (6; 4); (6; 5); (6; 6).

⇒ C = {(1; 2); (1; 4); (1; 6); (2; 1); (2; 2); (2; 3); (2; 4); (2; 5); (2; 6); (3; 2); (3; 4); (3; 6); (4; 1); (4; 2); (4; 3); (4; 4); (4; 5); (4; 6); (5; 2); (5; 4); (5; 6); (6; 1); (6; 2); (6; 3); (6; 4); (6; 5); (6; 6)}.

⇒ n(C) = 27.

⇒ P(C) = $\frac{n\left(C\right)}{n\left(\Omega \right)}$= $\frac{27}{36}$ = $\frac{3}{4}$.

Vậy xác suất của biến cố C là $\frac{3}{4}$.

15. Một số khái niệm về xác suất

a. Phép thử ngẫu nhiên và không gian mẫu

Có những phép thử mà ta không thể đoán được kết quả của nó, mặc dù đã biết tập hợp các kết quả có thể của phép thử đó. Những phép thử như thế gọi là phép thử ngẫu nhiên (gọi tắt là phép thử).

Tập hợp Ω các kết quả có thể xảy ra của một phép thử gọi là không gian mẫu của phép thử đó.

Ví dụ: Viết không gian mẫu của phép thử tung một đồng xu ba lần.

Hướng dẫn giải

Khi tung một đồng xu thì có hai kết quả có thể là đồng xu xuất hiện mặt sấp (S) hoặc đồng xu xuất hiện mặt ngửa (N).

Khi đó, tung ba đồng xu thì có các kết quả có thể là: SSS; SSN; SNN; SNS; NSS; NSN; NNS; NNN.

Suy ra không gian mẫu của phép thử là Ω = {SSS; SSN; SNN; SNS; NSS; NSN; NNS; NNN}.

Vậy không gian mẫu của phép thử tung đồng xu ba lần là: Ω = {SSS; SSN; SNN; SNS; NSS; NSN; NNS; NNN}.

b. Biến cố

* Định nghĩa

Nhận xét:

- Mỗi sự kiện liên quan đến phép thử T tương ứng với một (và chỉ một) tập con A của không gian mẫu Ω.

- Ngược lại, mỗi tập con A của không gian mẫu Ω có thể phát biểu dưới dạng mệnh đề nêu sự kiện liên quan đến phép thử T.

Định nghĩa:

Biến cố ngẫu nhiên (gọi tắt là biến cố) là một tập con của không gian mẫu.

Chú ý: Vì sự kiện chỉ ra tính chất đặc trưng cho các phần tử của một biến cố nên ta cũng gọi sự kiện là biến cố. Chẳng hạn “Kết quả của hai lần tung là giống nhau” trong phép thử “Tung một đồng xu hai lần liên tiếp” là một biến cố.

Ví dụ: Với phép thử tung đồng xu ba lần liên tiếp. Biến cố A: “Có ít nhất hai lần xuất hiện mặt sấp” là tập con nào của không gian mẫu.

Hướng dẫn giải

Phép thử tung đồng xu ba lần có không gian mẫu là: Ω = {SSS; SSN; SNN; SNS; NSS; NSN; NNS; NNN}.

Khi đó, biến cố A tương ứng với tập con {SSS; SSN; SNS; NSS}.

Vậy A = {SSS; SSN; SNS; NSS}.

* Biến cố không. Biến cố chắc chắn

Xét phép thử T với không gian mẫu Ω. Mỗi biến cố là một tập con của tập Ω. Vì thế, tập hợp ∅ cũng là một biến cố, gọi là biến cố không thể (gọi tắt là biến cố không). Còn tập hợp Ω gọi là biến cố chắc chắn.

Ví dụ: Khi gieo một con xúc xắc hai lần liên tiếp. Biến cố A: “Tổng số chấm của hai lần gieo bằng 1” là biến cố không. Biến cố B: “Tổng số chấm hai lần gieo nhỏ hơn 13” là biến cố chắc chắn.

* Biến cố đối

Tập con Ω\A xác định một biến cố, gọi là biến cố đối của biến cố A, kí hiệu là $\overline{A}$ .

Chú ý: Nếu biến cố A được mô tả dưới dạng mệnh đề toán học Q thì biến cố đối $\overline{A}$ được mô tả bằng mệnh đề phủ định của mệnh đề Q (tức là mệnh đề $\overline{Q}$ ).

Ví dụ: Xét phép thử “Tung một đồng xu”. Hãy xác định biến cố đối của biến cố A: “Đồng xu xuất hiện mặt ngửa”.

Hướng dẫn giải

Khi tung một đồng xu thì sẽ xuất hiện mặt sấp (S) hoặc mặt ngửa (N).

Khi đó biến cố đối của biến cố A: “Đồng xu xuất hiện mặt ngửa” là $\overline{A}$: “Đồng xu xuất hiện mặt sấp”.

Vậy biến cố đối của biến cố A là $\overline{A}$: “Đồng xu xuất hiện mặt sấp”.

c. Xác suất của biến cố

Xác suất của biến cố A, kí hiệu là P(A), bằng tỉ số $\frac{n\left(A\right)}{n\left(\Omega \right)}$, ở đó n(A), n(Ω) lần lượt là số phần tử của hai tập hợp A và Ω. Như vậy P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$.

Ví dụ: Với phép thử tung đồng xu ba lần liên tiếp. Tính xác suất của biến cố A: “Có ít nhất hai lần xuất hiện mặt sấp”.

Hướng dẫn giải

Phép thử tung đồng xu ba lần có không gian mẫu là: Ω = {SSS; SSN; SNN; SNS; NSS; NSN; NNS; NNN}.

⇒ n(Ω) = 8.

Khi đó, các kết quả thuận lợi cho biến cố A là: SSS; SSN; SNS; NSS.

⇒ A = {SSS; SSN; SNS; NSS}.

⇒ n(A) = 4.

⇒ P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}$ = $\frac{4}{8}$ = $\frac{1}{2}$.

Vậy xác suất của biến cố A: “Có ít nhất hai lần xuất hiện mặt sấp” là $\frac{1}{2}$.

16. Tính chất của xác suất

Xét phép thử T với không gian mẫu là Ω. Khi đó, ta có các tính chất sau:

+) P(∅) = 0; P(Ω) = 1;

+) 0 ≤ P(A) ≤ 1 với mỗi biến cố A;

+) $P\left(\overline{A}\right)=1-P\left(A\right)$ với mỗi biến cố A.

Ví dụ: Trong túi có 3 quả bóng màu xanh và 2 quả bóng màu vàng, các quả bóng có kích thước và khối lượng giống nhau. Lấy đồng thời ngẫu nhiên 2 quả bóng.

Tính xác suất cuả các biến cố:

A: “Hai quả bóng lấy ra không phải màu xanh và màu vàng”.

B: “Hai quả bóng lấy ra là màu xanh hoặc màu vàng”.

C: “Hai quả bóng lấy ra khác màu”.

Hướng dẫn giải

Do trong túi chỉ có hai loại bóng màu xanh và màu vàng nên khi lấy ngẫu nhiên hai quả bóng trong túi thì hai quả bóng lấy ra phải là bóng màu xanh hoặc màu vàng.

Do đó biến cố A: “Hai quả bóng lấy ra không phải màu xanh và màu vàng” là biến cố không thể, tức là A = ∅.

Suy ra P(A) = P(∅) = 0.

Biến cố B: “Hai quả bóng lấy ra là màu xanh hoặc màu vàng” luôn luôn xảy ra.

⇒ B = Ω

⇒ P(B) = P(Ω) = 1.

Ta có 3 quả bóng màu xanh, 2 quả bóng màu vàng, nên trong túi có 3 + 2 = 5 quả bóng.

Khi lấy ngẫu nhiên ra 2 trong 5 quả bóng, ta có $C_5^2=10$ (cách).

Suy ra không gian mẫu Ω có 10 phần tử.

⇒ n(Ω) = 10.

Xét biến cố C: “Hai quả bóng lấy ra khác màu”.

Ta có biến cố đối của C là $\overline{C}$: “Hai quả bóng lấy ra cùng màu”.

Suy ra hai quả bóng lấy ra cùng là màu xanh hoặc cùng là màu vàng.

+ Hai quả bóng lấy ra cùng là màu xanh, tức là lấy được 2 trong 3 quả bóng màu xanh,  có $C_3^2=3$ (cách).

+  Hai quả bóng lấy ra cùng là màu vàng, tức là lấy được 2 trong 2 quả bóng màu vàng,  có $C_2^2=1$ (cách).

Suy ra số cách lấy được hai quả bóng cùng màu là: 3 + 1 = 4 (cách)

⇒ $n\left(\overline{C}\right)$ = 4.

⇒ $P\left(\overline{C}\right)=\frac{n\left(\overline{C}\right)}{n\left(\Omega \right)}$ = $\frac{4}{10}$ = $\frac{2}{5}$.

Mặt khác $P\left(\overline{C}\right)=1-P\left(C\right)$ 

⇒ P(C) = 1 – $P\left(\overline{C}\right)$ = 1 – $\frac{2}{5}$ = $\frac{3}{5}$.

Vậy xác xuất của biến cố C là $\frac{3}{5}$.

17. Nguyên lí xác suất bé

- Nếu một biến cố ngẫu nhiên có xác suất rất bé thì thực tế có thể cho rằng trong một phép thử biến cố đó sẽ không xảy ra.

- Một xác suất như thế nào được xem là bé phải tùy thuộc vào từng bài toán cụ thể.

Ví dụ:

- Mỗi chuyến bay đều có một xác suất rất bé bị xảy ra tai nạn. Nhưng thực tế, tai nạn của một chuyến bay gần như sẽ không xảy ra.

- Xác suất để dù không mở là 0,01(dùng cho nhảy dù) thì không thể coi là bé và không thể dùng loại dù đó. Xác suất để tàu về ga chậm là 0,01 thì có thể xem là tàu về ga đúng giờ.