Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài tập cuối chương 6 chi tiết sách Toán 7 Tập 2 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Bài tập cuối chương 6

Giải Toán 7 trang 68 Tập 2

Bài 1 trang 68 Toán 7 Tập 2: Biểu thức nào sau đây là đa thức một biến? Tìm biến và bậc của đa thức đó.

a) -7x + 5.

b) 2 021x2 - 2 022x + 2 023.

c) 2y3 - $\frac{3}{y+2}$ + 4.

d) -2tm + 8t2 + t - 1, với m là số tự nhiên lớn hơn 2.

Lời giải:

a) Biểu thức -7x + 5 là đa thức một biến x, đa thức này có bậc bằng 1.

b) Biểu thức 2 021x2 - 2 022x + 2 023 là đa thức một biến x, đa thức này có bậc bằng 2.

c) Biểu thức 2y3 - $\frac{3}{y+2}$ + 4 không phải đa thức do có chứa biến ở dưới mẫu.

d) Biểu thức -2tm + 8t2 + t - 1 là đa thức một biến t, đa thức này có bậc bằng m, với m là số tự nhiên lớn hơn 2.

Bài 2 trang 68 Toán 7 Tập 2: Tính giá trị của biểu thức:

a) A = -5a - b - 20 tại a = -4, b = 18;

b) B = -8xyz + 2xy + 16y tại x = -1, y = 3, z = -2;

c) C = -x2021y2 + 9x2021 tại x = -1, y = -3.

Lời giải:

a) Thay a = -4, b = 18 vào biểu thức A = -5a - b - 20 ta được:

A = -5.(-4) - 18 - 20

A = 20 - 18 - 20

A = -18.

Vậy A = -18 khi a = -4, b = 18.

b) Thay x = -1, y = 3, z = -2 vào biểu thức B = -8xyz + 2xy + 16y ta được:

B = -8.(-1).3.(-2) + 2.(-1).3 + 16.3

B = -48 + (-6) + 48

B = -6.

Vậy B = -6 khi x = -1, y = 3, z = -2.

c) Thay x = -1, y = -3 vào biểu thức C = -x2021y2 + 9x2021 ta được:

C = - (-1)2021 .(-3)2 + 9.(-1)2021 

C = -(-1) . 9 + 9 . (-1)

C = 1.9 + (‒9)

C = 9 + (-9)

C = 0.

Vậy C = 9 khi x = -1, y = -3.

Bài 3 trang 68 Toán 7 Tập 2: Viết đa thức trong mỗi trường hợp sau:

a) Đa thức bậc nhất có hệ số của biến bằng -2 và hệ số tự do bằng 6;

b) Đa thức bậc hai có hệ số tự do bằng 4;

c) Đa thức bậc bốn có hệ số của lũy thừa bậc 3 của biến bằng 0;

d) Đa thức bậc sáu trong đó tất cả hệ số của lũy thừa bậc lẻ của biến đều bằng 0.

Lời giải:

a) Đa thức cần tìm là đa thức bậc nhất nên số mũ cao nhất của biến là 1.

Đa thức có hệ số của biến bằng -2 và hệ số tự do bằng 6 nên đa thức bậc nhất cần tìm là: -2x + 6.

b) Đa thức cần tìm là đa thức bậc hai nên số mũ cao nhất của biến là 2 và hệ số của luỹ thừa bậc 2 của biến là một số tuỳ ý khác 0.

Đa thức có hệ số của luỹ thừa bậc 1 của biến là một số tùy ý (do đề bài không đề cập đến) và hệ số tự do bằng 4.

Khi đó đa thức cần tìm có dạng ax2 + bx + 4 với a, b ∈ ℝ và a ≠ 0.

Chẳng hạn, ta có đa thức cần tìm có thể là x2 + x + 4; 2x2 + 4;…

c) Đa thức cần tìm là đa thức bậc bốn nên số mũ cao nhất của biến là 4 và hệ số của luỹ thừa bậc 4 của biến là một số tuỳ ý khác 0.

Đa thức có hệ số của lũy thừa bậc 3 của biến bằng 0 và hệ số của lũy thừa bậc 2, bậc 1 của biến là một số tùy ý, hệ số tự do là một số tùy ý.

Khi đó đa thức cần tìm có dạng ax4 + bx2 + cx + d với a, b, c, d ∈ ℝ và a ≠ 0.

Chắng hạn, ta có đa thức cần tìm có thể là: x4; x4 + 2x2 + 3x + 4;…

d) Đa thức cần tìm là đa thức bậc sáu nên số mũ cao nhất của biến là 6 và hệ số của luỹ thừa bậc 6 là một số tùy ý khác 0.

Trong đa thức này tất cả hệ số của lũy thừa bậc lẻ của biến đều bằng 0 và hệ số các lũy thừa bậc chẵn còn lại của đa thức là một số tùy ý, hệ số tự do là một số tùy ý.

Khi đó đa thức cần tìm có dạng ax6 + bx4 + cx2 + d với a, b, c, d ∈ ℝ và a ≠ 0.

Chẳng hạn, ta có đa thức cần tìm có thể là 2x6 + 3; x6 + 2x2;…

Bài 4 trang 68 Toán 7 Tập 2: Kiểm tra xem trong các số -1, 0, 1, 2, số nào là nghiệm của mỗi đa thức sau:

a) 3x - 6;

b) x4 - 1;

c) 3x2 - 4x;

d) x2 + 9.

Lời giải:

a) Ta thay lần lượt các giá trị x = -1, x = 0, x = 1, x = 2 vào đa thức 3x - 6 để kiểm tra số nào là nghiệm của đa thức đó.

+ Thay x = -1 vào đa thức ta được: 3.(-1) - 6 = -3 - 6 = -9 ≠ 0.

Do đó số -1 không là nghiệm của đa thức 3x - 6.

+ Thay x = 0 vào đa thức ta được: 3.0 - 6 = 0 - 6 = -6 ≠ 0.

Do đó số 0 không là nghiệm của đa thức 3x - 6.

+ Thay x = 1 vào đa thức ta được: 3.1 - 6 = 3 - 6 = -3 ≠ 0.

Do đó số 1 không là nghiệm của đa thức 3x - 6.

+ Thay x = 2 vào đa thức ta được: 3.2 - 6 = 6 - 6 = 0.

Do đó số 2 là nghiệm của đa thức 3x - 6.

Vậy trong các số -1, 0, 1, 2 thì số 2 là nghiệm của đa thức 3x - 6.

b) Ta thay lần lượt các giá trị x = -1, x = 0, x = 1, x = 2 vào đa thức x4 - 1 để kiểm tra số nào là nghiệm của đa thức đó.

+ Thay x = -1 vào đa thức x4 - 1 ta được: (-1)4 - 1 = 1 - 1 = 0.

Do đó số -1 là nghiệm của đa thức x4 - 1.

+ Thay x = 0 vào đa thức x4 - 1 ta có: 04 - 1 = -1 ≠ 0.

Do đó số 0 không là nghiệm của đa thức x4 - 1.

+ Thay x = 1 vào đa thức x4 - 1 ta có: 14 - 1 = 0.

Do đó số 1 là nghiệm của đa thức x4 - 1.

+ Thay x = 2 vào đa thức x4 - 1 ta có: 24 - 1 = 16 - 1 = 15 ≠ 0.

Do đó số 2 không là nghiệm của đa thức x4 - 1.

Vậy trong các số -1, 0, 1, 2 thì số - 1 và số 1 là nghiệm của đa thức x4 - 1.

c) Ta thay lần lượt các giá trị x = -1, x = 0, x = 1, x = 2 vào đa thức 3x2 - 4x để kiểm tra số nào là nghiệm của đa thức đó.

+ Thay x = -1 vào đa thức trên ta được: 3.(-1)2 - 4.(-1) = 3 + 4 = 7 ≠ 0.

Do đó số -1 không là nghiệm của đa thức 3x2 - 4x.

+ Thay x = 0 vào đa thức trên ta được : 3.02 - 4.0 = 0.

Do đó số 0 là nghiệm của đa thức 3x2 - 4x.

+ Thay x = 1 vào đa thức trên ta có: 3.12 - 4.1 = 3 - 4 = -1 ≠ 0.

Do đó số 1 không là nghiệm của đa thức 3x2 - 4x.

+ Thay x = 2 vào đa thức trên ta có: 3 . 22 - 4 . 2 = 12 - 8 = 4 ≠ 0.

Do đó số 2 không là nghiệm của đa thức x4 - 1 .

Vậy trong các số -1, 0, 1, 2 thì số 0 là nghiệm của đa thức 3x2 - 4x.

d) Ta thay lần lượt các giá trị x = -1, x = 0, x = 1, x = 2 vào đa thức x2 + 9 để kiểm tra số nào là nghiệm của đa thức đó.

+ Thay x = -1 vào đa thức trên ta có: (-1)2 + 9 = 10 ≠ 0.

Do đó số -1 không là nghiệm của đa thức x2 + 9.

+ Thay x = 0 vào đa thức trên ta có: 02+ 9 = 9 ≠ 0.

Do đó số 0 không là nghiệm của đa thức x2 + 9.

+ Thay x = 1 vào đa thức trên ta có: 12 + 9 = 10 ≠ 0.

Do đó số 1 không là nghiệm của đa thức x2 + 9.

+ Thay x = 2 vào đa thức trên ta có: 22 + 9 = 13 ≠ 0.

Do đó số 2 không là nghiệm của đa thức x2 + 9.

Vậy trong các số -1, 0, 1, 2 thì không có số nào là nghiệm của đa thức x2 + 9.

Bài 5 trang 68 Toán 7 Tập 2: Cho đa thức P(x) = -9x6 + 4x + 3x5 + 5x + 9x6- 1.

a) Thu gọn đa thức P(x).

b) Tìm bậc của đa thức P(x).

c) Tính giá trị của đa thức P(x) tại x = -1; x = 0; x = 1.

Lời giải:

a) Thu gọn đa thức P(x):

P(x) = -9x6 + 4x + 3x5 + 5x + 9x6 - 1

P(x) = (-9x6 + 9x6) + 3x5 + (4x + 5x) - 1

P(x) = 3x5 + 9x - 1.

b) Đa thức P(x) có số mũ cao nhất của biến là 5 nên bậc của đa thức P(x) bằng 5.

c) Với P(x) = 3x5 + 9x - 1:

+ Thay x = ‒1 vào đa thức ta có:

P(-1) = 3.(-1)5 + 9.(-1) - 1 = 3.(-1) + (-9) - 1 = -3 - 9 - 1 = -13.

+ Thay x = 0 vào đa thức ta có:

P(0) = 3.05 + 9.0 - 1 = 0 + 0 -1 = -1.

+ Thay x = 1 vào đa thức ta có:

P(1) = 3.15 + 9.1 - 1 = 3 + 9 - 1 = 11.

Vậy P(-1) = -13; P(0) = -1 và P(1) = 11.

Bài 6 trang 68 Toán 7 Tập 2: Tính:

a) -2x2 + 6x2;

b) 4x3 - 8x3;

c) 3x4(-6x2);

d) (-24x6) : (-4x3).

Lời giải:

a) -2x2 + 6x2 = (-2 + 6).x2 = 4x2.

b) 4x3 - 8x3 = (4 - 8).x3 = -4x3.

c) 3x4(-6x2) = 3.(-6).x4.x2 = -18x4+2 = -18x6.

d) (-24x6) : (-4x3) = [-24 : (-4)].(x6 : x3) = 6x6-3 = 6x3.

Bài 7 trang 68 Toán 7 Tập 2: Tính:

a) (x2 + 2x + 3) + (3x2 - 5x + 1);

b) (4x3 - 2x2 - 6) - (x3 - 7x2 + x - 5);

c) -3x2(6x2 - 8x + 1);

d) (4x2 + 2x + 1)(2x - 1);

e) (x6 - 2x4 + x2) : (-2x2);

g) (x5 - x4 - 2x3) : (x2 + x).

Lời giải:

a) (x2 + 2x + 3) + (3x2 - 5x + 1)

= x2 + 2x + 3 + 3x2 - 5x + 1

= (x2 + 3x2) + (2x - 5x) + (3 + 1)

= (1 + 3)x2 + (2 – 5)x + 4

= 4x2 - 3x + 4.

b) (4x3 - 2x2 - 6) - (x3 - 7x2 + x - 5)

= 4x3 - 2x2 - 6 - x3 + 7x2 - x + 5

= (4x3 - x3) + (-2x2 + 7x2) - x + (-6 + 5)

= (4 – 1)x3 + (‒2 + 7)x2 – x ‒ 1

= 3x3 + 5x2 - x - 1.

c) -3x2(6x2 - 8x + 1)

= -3x2.6x2 - (-3x2).8x + (-3x2).1

= (-3).6.x2+2 – (–3).8.x2+1 + (–3).1.x2

= -18x4 - (-24)x3 + (-3)x2

= - 18x4 + 24x3 - 3x2.

d) (4x2 + 2x + 1)(2x - 1)

= 4x2.2x - 4x2.1 + 2x.2x - 2x.1 + 1.2x - 1.1

= 4.2.x2+1 - 4.1.x2 + 2.2.x1+1 - 2x + 2x - 1

= 8x3 - 4x2 + 4x2 + (-2x + 2x) - 1

= 8x3 + (-4x2 + 4x2) - 1

= 8x3 - 1.

e) (x6 - 2x4 + x2) : (-2x2)

= x6 : (-2x2) - 2x4 : (-2x2) + x2 : (-2x2)

= $\frac{1}{-2}{x}^{6-2}-\frac{2}{-2}{x}^{4-2}+\frac{1}{-2}{x}^{2-2}$

= $\frac{-1}{2}{x}^4+x^2-\frac{1}{2}{x}^0$

$=\frac{-1}{2}{x}^4+x^2-\frac{1}{2}$

g) Thực hiện phép chia đa thức ta được:

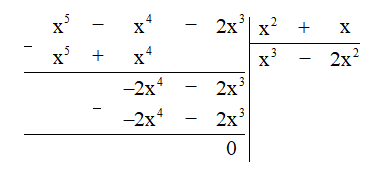
Vậy (x5 - x4 - 2x3) : (x2 + x) = x3 - 2x2.

Giải Toán 7 trang 69 Tập 2

Bài 8 trang 69 Toán 7 Tập 2: Cho hai đa thức: A(x) = 4x4 + 6x2 - 7x3 - 5x - 6 và B(x) = -5x2 + 7x3 + 5x + 4 - 4x4.

a) Tìm đa thức M(x) sao cho M(x) = A(x) + B(x).

b) Tìm đa thức C(x) sao cho A(x) = B(x) + C(x).

Lời giải:

a) M(x) = A(x) + B(x)

= (4x4 + 6x2 - 7x3 - 5x - 6) + (-5x2 + 7x3 + 5x + 4 - 4x4)

= 4x4 + 6x2 - 7x3 - 5x - 6 - 5x2 + 7x3 + 5x + 4 - 4x4

= (4x4 - 4x4) + (-7x3 + 7x3) + (6x2 - 5x2) + (-5x + 5x) + (-6 + 4)

= 0.x4 + 0.x3 + (6 – 5).x2 + 0.x + (‒2)

= x2 - 2.

Vậy M(x) = x2 - 2.

b) Ta có: A(x) = B(x) + C(x)

Suy ra C(x) = A(x) - B(x)

= (4x4 + 6x2 - 7x3 - 5x - 6) - (-5x2 + 7x3 + 5x + 4 - 4x4)

= 4x4 + 6x2 - 7x3 - 5x - 6 + 5x2 - 7x3 - 5x - 4 + 4x4

= (4x4 + 4x4) + (-7x3 - 7x3) + (6x2 + 5x2) + (-5x - 5x) + (-6 - 4)

= (4 + 4).x4 + (-7 - 7).x3 + (6 + 5).x2 + (-5 - 5).x + (-10)

= 8x4 - 14x3 + 11x2 - 10x - 10.

Vậy C(x) = 8x4 - 14x3 + 11x2 - 10x - 10.

Bài 9 trang 69 Toán 7 Tập 2: Cho P(x) = x3 + x2 + x + 1 và Q(x) = x4 - 1. Tìm đa thức A(x) sao cho P(x).A(x) = Q(x).

Lời giải:

Ta có: P(x).A(x) = Q(x)

Suy ra A(x) = Q(x) : P(x).

Thực hiện phép chia đa thức ta được:

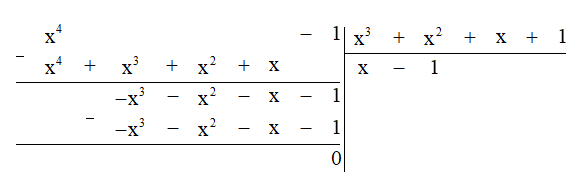
Do đó Q(x) : P(x) = x – 1

Vậy A(x) = x - 1.

Bài 10 trang 69 Toán 7 Tập 2: Nhân dịp lễ Giáng sinh, một cửa hàng bán quần áo trẻ em thông báo khi mua mỗi bộ quần áo sẽ được giảm giá 30% so với giá niêm yết. Giả sử giá niêm yết một bộ quần áo là x (đồng). Viết biểu thức tính số tiền phải trả khi mua loại quần áo đó với số lượng:

a) 1 bộ;

b) 3 bộ;

c) y bộ.

Lời giải:

Do mỗi bộ quần áo được giảm giá 30% so với giá niêm yết (x đồng) nên giá sau khi đã giảm sẽ bằng 100% - 30% = 70% giá niêm yết.

Vậy ta có giá một bộ quần áo sau khi giảm 30% là: 70% . x = 0,7.x (đồng).

a) Số tiền phải trả khi mua 1 bộ là: 0,7x.1 = 0,7x (đồng).

Vậy biểu thức tính số tiền khi mua 1 bộ loại quần áo đó là 0,7x đồng.

b) Số tiền phải trả khi mua 3 bộ là: 0,7x.3 = 2,1x (đồng).

Vậy biểu thức tính số tiền khi mua 3 bộ loại quần áo đó là 2,1x đồng.

c) Số tiền phải trả khu mua y bộ là: 0,7xy (đồng).

Vậy biểu thức tính số tiền khi mua y bộ loại quần áo đó là 0,7xy đồng.

Bài 11 trang 69 Toán 7 Tập 2: Một doanh nghiệp kinh doanh cà phê cho biết: Sau khi rang xong, khối lượng cà phê giảm 12% so với trước khi rang.

a) Tìm số thích hợp cho $\boxed{?}$ ở bảng sau:

 

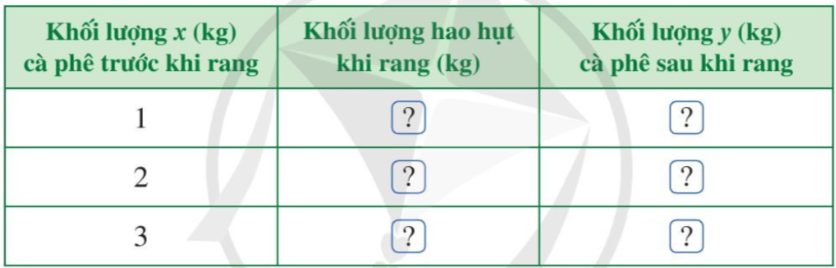
b) Tìm công thức chỉ mối liên hệ giữa x và y.

c) Để có được 2 tấn cà phê sau khi rang thì doanh nghiệp đó cần sử dụng bao nhiêu tấn cà phê trước khi rang?

Lời giải:

a) - Khối lượng cà phê trước khi rang là 1 kg thì:

 + Khối lượng hao hụt khi rang là: 1.12% = 0,12 kg;

+ Khối lượng cà phê sau khi rang là: 1 - 0,12 = 0,88 kg.

- Khối lượng cà phê trước khi rang là 2 kg thì:

+ Khối lượng hao hụt khi rang là: 2.12% = 0,24 kg;

+ Khối lượng cà phê sau khi rang là: 2 - 0,24 = 1,76 kg.

- Khối lượng cà phê trước khi rang là 3 kg thì:

+ Khối lượng hao hụt khi rang là: 3.12% = 0,36 kg;

+ Khối lượng cà phê sau khi rang là: 3 - 0,36 = 2,64 kg.

Ta có bảng sau:

b) Sau khi rang xong, khối lượng cà phê giảm 12% so với trước khi rang nên khối lượng cà phê sau khi rang bằng 100% - 12% = 88% khối lượng cà phê lúc đầu.

Do đó: y = 88%x = 0,88x.

Vậy công thức chỉ mối liên hệ giữa x và y là: y = 0,88x.

c) Số tấn cà phê cần dùng để có được 2 tấn cà phê sau khi rang là:

2 : 88% = 2 : $\frac{88}{100}$ = 2 . $\frac{100}{88}$ = $\frac{25}{11}$ ≈ 2,27 tấn.

Vậy doanh nghiệp đó cần sử dụng khoảng 2,27 tấn cà phê trước khi rang để thu được 2 tấn cà phê sau khi rang.

Bài 12 trang 69 Toán 7 Tập 2: Một công ty sau khi tăng giá 50 nghìn đồng mỗi sản phẩm so với giá ban đầu là x (nghìn đồng) với x < 60 thì có doanh thu là -5x2 + 50x + 15 000 (nghìn đồng). Tính số sản phẩm mà công ty đã bán được theo x.

Lời giải:

Sau khi tăng giá 50 nghìn đồng mỗi sản phẩm so với giá ban đầu là x (nghìn đồng) (x < 60) thì giá của mỗi sản phẩm sau khi tăng giá là x + 50 (nghìn đồng).

Khi đó số sản phẩm đã bán được là: (-5x2 + 50x + 15 000) : (x + 50)

Thực hiện phép chia đa thức ta được:

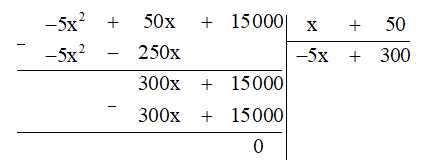
Do đó (-5x2 + 50x + 15 000) : (x + 50) = ‒5x + 300

Vậy công ty đã bán được -5x + 300 sản phẩm với x < 60.

Bài 13 trang 69 Toán 7 Tập 2: Một công ty du lịch dự định dùng 2 xe ô tô để chở khách đi tham quan, mỗi xe chở tối đa 35 khách, mức giá cho chuyến đi là 900 nghìn/người và đã có 50 người đăng kí tham quan. Công ty đặt chính sách khuyến mãi như sau: Sẽ giảm giá cho mỗi người trong đoàn tham quan là 10 nghìn đồng khi cứ có thêm 1 khách tham quan ngoài 50 khách trên.

a) Giả sử số khách tham quan thêm là x (x ≤ 20). Tính số tiền mà công ty thu được theo x.

b) Nếu 2 xe ô tô của công ty đều chở tối đa số khách thì số tiền công ty thu được tổng cộng là bao nhiêu?

Lời giải:

a) Số tiền giảm giá cho mỗi người khi có thêm x khách tham quan là: 10x (nghìn đồng).

Khi đó số tiền mỗi người cần trả khi được giảm giá là: 900 - 10x (nghìn đồng).

Ban đầu có 50 khách, có thêm x khách thì tổng số khách tham quan là x + 50 (khách).

Số tiền công ty thu được là (x + 50)(900 - 10x) (nghìn đồng).

b) Mỗi xe được chở tối đa 35 khách nên nếu cả 2 xe ô tô đều chở tối đa khách thì tổng số khách tham quan là: 2.35 = 70 (khách).

Khi đó có thêm 20 khách so với 50 khách ban đầu.

Tức là ta có x = 20.

Thay x = 20 vào biểu thức (x + 50)(900 - 10x) ta có số tiền công ty thu được là:

(20 + 50). (900 – 10.20) = 70.(900 – 200) = 70.700 = 49 000 (nghìn đồng) = 49 triệu đồng.

Vậy công ty thu được tổng cộng là 49 triệu đồng.

Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:

Giải SGK Toán 7 Bài 4: Phép nhân đa thức một biến

Giải SGK Toán 7: Bài tập cuối chương 6

Giải SGK Toán 7 Bài 1: Tổng các góc của một tam giác

Giải SGK Toán 7 Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

Giải SGK Toán 7 Bài 3: Hai tam giác bằng nhau

Lý thuyết Toán 7 Chương 6: Biểu thức đại số

1. Biểu thức số

– Các số được nối với nhau bởi dấu các phép tính (cộng, trừ, nhân, chia, nâng lên luỹ thừa) tạo thành một biểu thức số. Đặc biệt, mỗi số cũng được coi là một biểu thức số.

– Trong biểu thức số có thể có các dấu ngoặc để chỉ thứ tự thực hiện các phép tính.

– Khi thực hiện các phép tính trong một biểu thức số, ta nhận được một số. Số đó được gọi là giá trị của biểu thức số đã cho.

Ví dụ: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) 2022 không phải là biểu thức số.

b) Biểu thức số phải có đầy đủ các phép tính cộng, trừ, nhân, chia, nâng lên luỹ thừa.

Hướng dẫn giải

a) Sai. Vì một số cũng được coi là một biểu thức số nên 2022 là biểu thức số.

b) Sai. Vì trong biểu thức số không nhất thiết phải có đầy đủ các phép tính cộng, trừ, nhân, chia, nâng lên luỹ thừa.

Chẳng hạn: 2² + 1 chỉ có phép nâng lên luỹ thừa và phép cộng cũng là một biểu thức số.

Ví dụ: Viết biểu thức số biểu thị:

a) Chu vi hình chữ nhật có chiều dài là 30 cm, chiều rộng là 20 cm.

b) Diện tích của hình tròn có bán kính 40 cm.

Hướng dẫn giải:

a) Biểu thức biểu thị chu vi hình chữ nhật có chiều dài 30 cm, chiều rộng 20 cm là:

2(30 + 20) (cm).

b) Biểu thức biểu thị diện tích hình tròn có bán kính 40 cm là: p. 40² (cm²).

Ví dụ: Một trường THCS cử một đoàn giáo viên tham gia tập huấn gồm: 1 trưởng đoàn, mỗi khối 6, 7, 8, 9 đều có 2 giáo viên toán, 1 giáo viên văn. Biểu thức số nào dưới đây biểu thị tổng số thành viên của đoàn?

a) 1 + 4. 2 + 1 (thành viên);

b) 1 + 4. (2 + 1) (thành viên).

Hướng dẫn giải

Biểu thức biểu thị số thành viên của mỗi khối là: 2 + 1 (thành viên).

Biểu thức biểu thị số thành viên của 4 khối là: 4. (2 + 1) (thành viên).

Biểu thức biểu thị tổng số thành viên của đoàn là: 1 + 4. (2 + 1) (thành viên).

2. Biểu thức đại số

– Biểu thức gồm các số và các biến số (đại diện cho số) được nối với nhau bởi các kí hiệu phép toán cộng, trừ, nhân, chia, nâng lên luỹ thừa được gọi là biểu thức đại số.

– Biểu thức số cũng là biểu thức đại số.

– Trong biểu thức đại số có thể có các dấu ngoặc để chỉ thứ tự thực hiện các phép tính.

– Chú ý: Để cho gọn, khi viết các biểu thức đại số ta thường:

+ Không viết dấu nhân giữa các chữ, cũng như giữa số và chữ.

Chẳng hạn: viết xy thay cho x.y; viết 2x thay cho 2.x.

+ Viết x thay cho 1. x; viết –x thay cho (–1). x.

– Trong biểu thức đại số, vì chữ đại diện cho số nên khi thực hiện các phép tính trên các chữ, ta có thể áp dụng những tính chất, quy tắc phép tính như trên các số.

Chẳng hạn:

2x + x = 3x;           5x – 2x = 3x;                             

x.x² = x³;                x + y = y + x;        

xy = yx;                 x(yz) = (xy)z;                            

x + (y + z) = (x + y) + z;           

x(y + z) = xy + xz;

–x(y – z) = –xy + xz; …

Ví dụ: Trong các biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) 2. 3 – 3. 5 là biểu thức đại số;

b) 3x² + 5x + 2 là biểu thức đại số;

c) 2x + 3y + z không phải là biểu thức đại số.

Hướng dẫn giải:

a) Đúng. Vì 2. 3 – 3. 5 là biểu thức số nên cũng là biểu thức đại số;

b) Đúng. Vì 3x² + 5x + 2 được nối với nhau bởi các phép toán và x đại diện cho số nên biểu thức này là biểu thức đại số.

c) Sai. Vì 2x + 3y + z được nối với nhau bởi các phép toán và x, y, z đại diện cho các số nên biểu thức này là biểu thức đại số.

Ví dụ: Viết biểu thức biểu thị diện tích toàn phần (tổng diện tích tất cả các mặt) của hình hộp chữ nhật có ba kích thước là 4 (cm), x (cm), y (cm) như hình vẽ dưới đây:

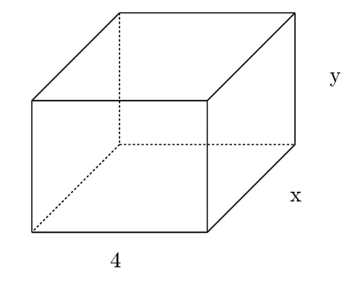
Hướng dẫn giải:

Diện tích xung quanh của hình hộp chữ nhật là:

2(4 + x). y (cm²)

Diện tích đáy của hình hộp chữ nhật là: 4x (cm²)

Diện tích toàn phần của hình hộp chữ nhật là:

2(4 + x). y + 2.4x (cm²)

Vậy biểu thức biểu thị diện tích toàn phần của hình hộp chữ nhật trên là: 2(4 + x). y + 2.4x (cm²).

3. Giá trị của biểu thức đại số

Để  tính  giá  trị  của  một  biểu  thức  đại  số  tại  những giá trị cho trước của các biến, ta thay các giá trị cho trước đó vào biểu thức rồi thực hiện các phép tính.

Ví dụ: Tính giá trị của biểu thức x² – 5y + 1 khi x = 4 và y = 2.

Hướng dẫn giải

Thay x = 4 và y = 2 vào biểu thức trên ta được:

4² – 5.2 + 1 = 16 – 10 + 1 = 7

Vậy khi x = 4 và y = 2 thì giá trị của biểu thức x² – 5y + 1 bằng 7.

Ví dụ: Bác Hoa mua một túi rau và một số quả cam. Biết rằng mỗi kilôgam cam có giá 40 nghìn đồng và túi rau có giá 15 nghìn đồng.

a) Hãy viết biểu thức biểu thị tổng số tiền bác Hoa phải trả nếu số cam bác Hoa mua là x kilôgam.

b) Giả sử số cam bác Hoa mua là 2,5 kilôgam. Sử dụng kết quả câu a, em hãy tính xem bác Hoa phải trả tất cả bao nhiêu tiền.

Hướng dẫn giải

a) Số tiền bác Hoa phải trả cho x kilôgam cam là 40x (nghìn đồng).

Số tiền bác Hoa phải trả cho một túi rau là 15 nghìn đồng.

Vậy biểu thức biểu thị tổng số tiền bác Hoa phải trả là:

40x + 15 (nghìn đồng)

b) Thay x = 2,5 vào biểu thức 40x + 15, ta được:

40. 2,5 + 15 = 115 (nghìn đồng)

Vậy bác Hoa phải trả tất cả là 115 nghìn đồng.

4. Đơn thức một biến. Đa thức một biến

4.1. Đơn thức một biến

– Đơn thức một biến là biểu thức đại số chỉ gồm một số hoặc một tích của một số với luỹ thừa có số mũ nguyên dương của biến đó.

Chẳng hạn: x², 2x³ là các đơn thức một biến x.

– Chú ý:

+ Mỗi đơn thức (một biến x) nếu không phải là một số thì có dạng ax^k, trong đó a là số thực khác 0 và k là số nguyên dương. Lúc đó, số a được gọi là hệ số của đơn thức ax^k.

+ Để thuận tiện cho việc thực hiện các phép tính (trên các đơn thức, đa thức, …), một số thực khác 0 được coi là đơn thức với số mũ của biến bằng 0.

Ví dụ: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) x + 1 là đơn thức một biến x;

b) 2x² là đơn thức một biến x;

c) 0 không là đơn thức một biến.

Hướng dẫn giải

a) Sai. Vì đơn thức một biến chỉ gồm một số hoặc một tích của một số với luỹ thừa của biến đó nên x² + 1 không phải là đơn thức một biến mà là đa thức một biến.

b) Đúng. Vì 2x² là tích của 2 với luỹ thừa 2 của biến x nên 2x² là đơn thức một biến x.

c) Sai. Vì một số cũng là đơn thức nên 0 là đơn thức một biến.

4.2. Đa thức một biến

– Đa thức một biến là tổng những đơn thức của cùng một biến.

Chẳng hạn: 3x² + 2x là đa thức của biến x.

– Chú ý:

+ Mỗi số được xem là một đa thức (một biến).

+ Số 0 được gọi là đa thức không.

+ Mỗi đơn thức cũng là một đa thức.

+ Thông thường ta kí hiệu đa thức một biến x là P(x), Q(x), A(x), B(x), …

Ví dụ: Biểu thức nào sau đây là đa thức một biến x?

a) x² – 9;

b) 2022;

c) 3x + y;

d) $\frac{25}{{\text{x}}^2}$+ 2x + 1.

Hướng dẫn giải

a) x² – 9 là đa thức một biến x vì là hiệu của 2 đơn thức một biến x là x² và 9.

b) 2022 là một số nên cũng được xem là một đa thức một biến.

c) 3x + y không phải là đa thức một biến x vì có cả biến y.

d) $\frac{25}{{\text{x}}^2}$+ 2x + 1 không phải là đa thức một biến x vì $\frac{25}{{\text{x}}^2}$ không phải là tích của một số với luỹ thừa có số mũ nguyên dương của biến x.

5. Cộng trừ đơn thức có cùng số mũ của biến

– Để cộng (trừ) hai đơn thức có cùng số mũ của biến, ta cộng (hay trừ) hai hệ số với nhau và giữ nguyên phần biến:

• ax^k + bx^k = (a + b)x^k;

• ax^k – bx^k = (a – b)x^k (k ∈ ℕ*).

Ví dụ: Thực hiện mỗi phép tính sau:

a) 13x² + 7x²;

b) 4x³ – 3x³;

c) a⁴ + 1,5a⁴ + 0,5a⁴.

Hướng dẫn giải

a) 13x² + 7x² = (13 + 7)x² = 20x²;

b) 4x³ – 3x³ = (4 – 3)x³ = 1.x³ = x³;

c) a⁴ + 1,5a⁴ + 0,5a⁴ = (1 + 1,5 + 0,5)a⁴ = 3a⁴.

6. Sắp xếp đa thức một biến

6.1. Thu gọn đa thức

Thu gọn đa thức một biến là làm cho đa thức đó không còn hai đơn thức nào có cùng số mũ của biến.

Ví dụ: Thu gọn đa thức:

a) P(x) = 3x² – 4x² + x³ + 3x³ – 4x + x + 1;

b) Q(x) = 2 – 3,5x⁴ – 5x² + 3x² + x + $\frac{7}{2}$x⁴ – 2x³ – 1.

Hướng dẫn giải

a) P(x) = 3x² – 4x² + x³ + 3x³ – 4x + x + 1

= (3 – 4)x² + (1 + 3)x³ + (–4 + 1)x + 1

= –x² + 4x³ – 3x + 1

Vậy dạng thu gọn của đa thức P(x) là –x² + 4x³ – 3x + 1.

b) Q(x) = 2 – 3,5x⁴ – 5x² + 3x² + x + $\frac{7}{2}$x⁴ – 2x³ – 1

= (2 – 1) + (–3,5x⁴ + $\frac{7}{2}$x⁴) + (– 5x² + 3x²) + x – 2x³

= 1 + $\left(-3,5+\frac{7}{2}\right)$x⁴ + (– 5 + 3)x² + x – 2x³

= 1 + 0x⁴ – 2x² + x – 2x³

 = 1 – 2x² + x – 2x³

Vậy dạng thu gọn của đa thức Q(x) là 1 – 2x² + x – 2x³.

6.2. Sắp xếp một đa thức

– Sắp xếp đa thức (một biến) theo số mũ giảm dần (hoặc tăng dần) của biến là sắp xếp các đơn thức trong dạng thu gọn của đa thức đó theo số mũ giảm dần (hoặc tăng dần) của biến.

– Chú ý: Trong dạng thu gọn của đa thức, hệ số của mỗi đơn thức được gọi là hệ số của đa thức đó.

Ví dụ: Sắp xếp đa thức A(x) = 3x² + 5x⁴ – x⁵ + 2x – 1 theo số mũ giảm dần của biến.

Hướng dẫn giải

A(x) = 3x² + 5x⁴ – x⁵ + 2x – 1

= –x⁵ + 5x⁴ + 3x² + 2x – 1.

Vậy sắp xếp đa thức A(x) theo số mũ giảm dần của biến ta được A(x) = –x⁵ + 5x⁴ + 3x² + 2x – 1.

Ví dụ: Cho đa thức P(x) = 3x² + 5x³ – 10x + 2x³ – 8x² + 9 + 6x.

Hãy thu gọn sau đó sắp xếp đa thức theo số mũ giảm dần của biến.

Hướng dẫn giải

P(x) = 3x² + 5x³ – 10x + 2x³ – 8x² + 9 + 6x

= (5x³ + 2x³) + (3x² – 8x²) + (–10x + 6x) + 9

= 7x³ – 5x² – 4x + 9

Vậy P(x) = = 7x³ – 5x² – 4x + 9.

7. Bậc của đa thức một biến

– Bậc của đa thức một biến (khác đa thức không, đa thu gọn) là số mũ cao nhất của biến trong đa thức đó.

– Chú ý:

+ Trong dạng thu gọn của đa thức, hệ số của luỹ thừa với số mũ cao nhất của biến còn gọi là hệ số cao nhất của đa thức; số hạng không chứa biến còn gọi là hệ số tự do của đa thức.

+ Một số khác 0 là đa thức bậc 0.

+ Đa thức không (số 0) không có bậc.

Ví dụ: Cho đa thức P(x) = x² + 2x² + 6x + 2x – 3.

a) Sắp xếp đa thức P(x) theo số mũ giảm dần của biến;

b) Tìm bậc của đa thức P(x);

c) Tìm hệ số cao nhất và hệ số tự do của đa thức P(x).

Hướng dẫn giải

a) P(x) = x² + 2x² + 6x + 2x – 3

= (x² + 2x²) + (6x + 2x) – 3

= (1 + 2)x² + (6 + 2)x – 3

= 3x² + 8x – 3

Vậy P(x) = 3x² + 8x – 3.

b) Bậc của đa thức P(x) là 2 vì số mũ cao nhất của x trong đa thức P(x) là 2.

c) Đa thức P(x) có hệ số cao nhất là 3 và hệ số tự do là –3.

8. Nghiệm của đa thức một biến

– Giá trị của đa thức P(x) tại x = a được kí hiệu là P(a).

– Nếu tại x = a, đa thức P(x) có giá trị bằng 0 thì a (hoặc x = a) gọi là một nghiệm của đa thức đó.

– Chú ý:

• x = a là nghiệm của đa thức P(x) nếu P(a) = 0.

• Một đa thức (khác đa thức không) có thể có một nghiệm, hai nghiệm, … hoặc không có nghiệm. Số nghiệm của một đa thức không vượt quá bậc của đa thức đó.

Ví dụ: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) x = 1 là nghiệm của đa thức A(x) = 2x – 2;

b) y = 3 là nghiệm của đa thức B(y) = 4y – 3;

c) z = 1 không là nghiệm của đa thức C(z) = z² + 1.

Hướng dẫn giải

a) Đúng. Vì A(1) = 2.1 – 2 = 0 nên x = 1 là nghiệm của đa thức A(x).

b) Sai. Vì B(3) = 4.3 – 3 = 9 ≠ 0 nên y = 3 không phải là nghiệm của B(y).

c) Đúng. Vì C(1) = 1² + 1 = 2 ≠ 0 nên z = 1 không phải là nghiệm của C(z).

Ví dụ: Cho P(x) = x² – 1. Tìm nghiệm của đa thức P(x).

Hướng dẫn giải

Ta có: P(x) = 0

Suy ra x² – 1 = 0

Do đó x² = 1

Hay x² = 1² = (–1)²

Suy ra x = 1 hoặc x = –1.

Vậy P(x) có nghiệm là x = 1, x = –1.

9. Phép cộng đa thức một biến

– Để cộng hai đa thức một biến (theo cột dọc), ta có thể làm như sau:

+ Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;

+ Đặt hai đơn thức có cùng số mũ của biến ở cùng cột;

+ Cộng hai đơn thức trong từng cột, ta có tổng cần tìm.

– Chú ý: Khi cộng đa thức theo cột dọc, nếu một đa thức khuyết số mũ nào của biến thì khi viết đa thức đó, ta bỏ trống cột tương ứng với số mũ trên.

Ví dụ: Cho hai đa thức: P(x) = x³ – 6x² + 1 và Q(x) = –3x² – 2x – 7. Tính tổng P(x) + Q(x) theo cột dọc.

Hướng dẫn giải

Ta thực hiện đặt phép tính cộng hai đa thức như sau:

$\begin{array}{l}\underset{¯}{+\begin{array}{c}\begin{array}{l}\mathrm{P}\left(\mathrm{x}\right)={\mathrm{x}}^3-6{\mathrm{x}}^2+1\\ \mathrm{Q}\left(\mathrm{x}\right)=-3{\text{x}}^2-2\mathrm{x}-7\end{array}\end{array}}\\ \mathrm{P}\left(\mathrm{x}\right)+\mathrm{Q}\left(\mathrm{x}\right)={\mathrm{x}}^3-9{\mathrm{x}}^2-2\mathrm{x}-6\end{array}$

Vậy P(x) + Q(x) = x³ – 9x² – 2x – 6.

– Để cộng hai đa thức một biến (theo hàng ngang), ta có thể làm như sau:

+ Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;

+ Viết tổng hai đã thức theo hàng ngang;

+ Nhóm các đơn thức có cùng số mũ của biến với nhau;

+ Thực hiện phép tính trong từng nhóm, ta được tổng cần tìm.

Ví dụ: Cho hai đa thức: P(x) = x³ – 6x² + 1 và Q(x) = –3x² – 2x – 7. Tính tổng P(x) + Q(x) theo hàng ngang.

Hướng dẫn giải

Ta có:

P(x) + Q(x) = (x³ – 6x² + 1) + (–3x² – 2x – 7)

= x³ – 6x² + 1 – 3x² – 2x – 7

= x³ + (– 6x² – 3x²) – 2x + (1 – 7)

= x³ – 9x² – 2x – 6.

Vậy P(x) + Q(x) = x³ – 9x² – 2x – 6.

10. Trừ hai đa thức một biến

– Để trừ đa thức P(x) cho đa thức Q(x) (theo cột dọc), ta có thể làm như sau:

+ Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;

+ Đặt hai đơn thức có cùng số mũ của biến ở cùng cột sao cho đơn thức của P(x) ở trên và đơn thức của Q(x) ở dưới;

+ Trừ hai đơn thức trong từng cột, ta có hiệu cần tìm.

Ví dụ: Cho M(x) = 5x⁴ + 7x³ – 2x và N(x) = –2x³ – 4x² + 6x + 8. Tính hiệu M(x) – N(x) theo cột dọc.

Hướng dẫn giải

Ta thực hiện đặt phép tính trừ hai đa thức như sau:

$\begin{array}{l}\underset{¯}{-\begin{array}{c}\begin{array}{l}\mathrm{M}\left(\mathrm{x}\right)=5{\mathrm{x}}^4+7{\mathrm{x}}^3–2\mathrm{x}\\ \mathrm{N}\left(\mathrm{x}\right)=–2{\mathrm{x}}^3–4{\mathrm{x}}^2+6\mathrm{x}+8\end{array}\end{array}}\\ \mathrm{M}\left(\mathrm{x}\right)-\mathrm{N}\left(\mathrm{x}\right)=5{\mathrm{x}}^4+9{\mathrm{x}}^3+4{\mathrm{x}}^2-8\mathrm{x}-8\end{array}$

Vậy M(x) – N(x) = 5x⁴ + 9x³ + 4x² – 8x – 8.

– Để trừ đa thức P(x) cho đa thức Q(x) (theo hàng ngang), ta có thể làm như sau:

+ Thu gọn mỗi đa thức và sắp xếp hai đa thức đó cùng theo số mũ giảm dần (hoặc tăng dần) của biến;

+ Viết hiệu P(x) – Q(x) theo hàng ngang, trong đó đa thức Q(x) được đặt trong dấu ngoặc;

+ Sau khi bỏ dấu ngoặc và đổi dấu mỗi đơn thức trong dạng thu gọn của đa thức Q(x), nhóm các đơn thức có cùng số mũ của biến với nhau;

+ Thực hiện phép tính trong từng nhóm, ta được hiệu cần tìm.

Ví dụ: Cho M(x) = 5x⁴ + 7x³ – 2x và N(x) = –2x³ – 4x² + 6x + 8. Tính hiệu M(x) – N(x) theo hàng ngang.

Hướng dẫn giải

Ta có:

M(x) – N(x) = (5x⁴ + 7x³ – 2x) – (–2x³ – 4x² + 6x + 8)

= 5x⁴ + 7x³ – 2x + 2x³ + 4x² – 6x – 8

= 5x⁴ + (7x² + 2x³) + 4x² + (–2x – 6x) – 8

= 5x⁴ + 9x³ + 4x² – 8x – 8

Vậy M(x) – N(x) = 5x⁴ + 9x³ + 4x² – 8x – 8.

Ví dụ: Xác định bậc của hai đa thức là tổng, hiệu của:

A(x) = –4x⁴ – 3x² + 7 và B(x) = 4x⁴ – 5x² + 8x – 1.

Hướng dẫn giải

Ta có:

• A(x) + B(x) = (–4x⁴ – 3x² + 7) + (4x⁴ – 5x² + 8x – 1)

= –4x⁴ – 3x² + 7 + 4x⁴ – 5x² + 8x – 1

= (–4x⁴ + 4x⁴) + (–3x² – 5x²) + 8x + (7 – 1)

= –8x² + 8x + 6

Do đó A(x) + B(x) = – 8x² + 8x + 6.

Vậy bậc của A(x) + B(x) là 2.

• A(x) – B(x) = (–4x⁴ – 3x² + 7) – (4x⁴ – 5x² + 8x – 1)

= –4x⁴ – 3x² + 7 – 4x⁴ + 5x² – 8x + 1

= (–4x⁴ – 4x⁴) + (–3x² + 5x²) – 8x + (7 + 1)

= –8x⁴ + 2x² – 8x + 8

A(x) + B(x) = –8x⁴ + 2x² – 8x + 8.

Vậy bậc của A(x) – B(x) là 4.

11. Nhân đơn thức với đơn thức

– Muốn nhân đơn thức A với đơn thức B, ta làm như sau:

+ Nhân hệ số của đơn thức A với hệ số của đơn thức B;

+ Nhân luỹ thừa của biến A với luỹ thừa của biến đó trong B;

+ Nhân các kết quả vừa tìm được với nhau.

– Tổng quát: Với a ≠ 0, b ≠ 0; m, n ∈ ℕ ta có:

ax^m. bxⁿ = a.b. x^m. xⁿ = abx^{m + n}.

Ví dụ: Tính:

a) 3x². 5x⁶;

b) – 4x³. 4x²;

c) 2x^{m + 2}. x^{n – 2} (m, n ∈ ℕ, n > 2).

Hướng dẫn giải

a) 3x². 5x⁶ = 3.5. x². x⁶ = 15x^{2 + 6} = 15x⁸;

b) – 4x³. 4x² = – 4.4. x³. x² = –16x^{3 + 2} = –16x⁵;

c) 2x^{m + 2}. x^{n – 2} = 2. x^{m + 2}. x^{n – 2} = 2x^{m + 2 + n – 2} = 2x^{m + n}.

12. Nhân đơn thức với đa thức

Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức đó với từng đơn thức của đa thức rồi cộng các tích với nhau.

A(B + C) = AB + AC

A(B – C) = AB – AC

Ví dụ: Tính:

a) x(2x + 1);

b) –2x²(2x² + 2x – 1);

c) –2x³($\frac{1}{2}$x² + 3x – 5).

Hướng dẫn giải

a) x(2x + 1) = x.2x + x.1 = 2x² + x;

b) –2x²(2x² + 2x – 1)

= –2x².2x² –2x².2x –2x².(–1)

= –4x⁴ – 4x³ + 2x²;

c) –2x³($\frac{1}{2}$x² + 3x – 5)

= –2x³.$\frac{1}{2}$x² –2x³.3x – 2x³.(–5)

= –x⁵ – 6x⁴ + 10x³.

13. Nhân đa thức với đa thức

– Muốn nhân một đa thức với một đa thức, ta nhân mỗi đơn thức của đa thức này với từng đơn thức của đa thức kia rồi cộng các tích với nhau.

(A + B)(C + D) = AC + AD + BC + BD

– Tích của hai đa thức là một đa thức.

– Sau khi thực hiện phép nhân hai đa thức, ta thường viết đa thức tích ở dạng thu gọn và sắp xếp các đơn thức theo số mũ tăng dần hoặc giảm dần của biến.

Ví dụ: Thực hiện phép nhân (4x – 3)(2x² – 5x + 6).

Hướng dẫn giải

Ta có: (4x – 3)(2x² – 5x + 6)

= 4x(2x² – 5x + 6) – 3(2x² – 5x + 6)

= 4x.2x² – 4x.5x + 4x.6 – 3.2x² – 3.(–5x) – 3.6

= 8x³ – 20x² + 24x – 6x² + 15x – 18

= 8x³ – 26x² + 39x – 18

Vậy (4x – 3)(2x² – 5x + 6) = 8x³ – 26x² + 39x – 18.

– Chúng ta có thể trình bày phép nhân đa thức theo cột dọc.

Chú ý: Khi thực hiện phép nhân hai đa thức theo cột dọc, các đơn thức có cùng số mũ (của biến) được xếp vào cùng một cột.

Ví dụ: Thực hiện phép nhân (4x – 3)(2x² – 5x + 6) theo cột dọc.

Hướng dẫn giải

Ta có: (4x – 3)(2x² – 5x + 6) = (2x² – 5x + 6).(4x – 3)

Thực hiện phép nhân theo cột dọc như sau:

$\begin{array}{l}\times \underset{¯}{\begin{array}{l}2{\mathrm{x}}^2-5\mathrm{x}+6\\ 4\mathrm{x}-3\end{array}}\\ \underset{¯}{\begin{array}{l}-6{\mathrm{x}}^2+15\mathrm{x}-18\\ 8{\mathrm{x}}^3-20{\mathrm{x}}^2+24\mathrm{x}\end{array}}\\ 8{\mathrm{x}}^3-26{\mathrm{x}}^2+39\mathrm{x}-18\end{array}$

Vậy (4x – 3)(2x² – 5x + 6) = 8x³ – 26x² + 39x – 18.

14. Chia đơn thức cho đơn thức

Muốn chia đơn thức A cho đơn thức B (B ≠ 0) khi số mũ của biến trong A lớn hơn hoặc bằng số mũ của biến đó trong B, ta làm như sau:

+ Chia hệ số của đơn thức A cho hệ số của đơn thức B.

+ Chia luỹ thừa của biến trong A cho luỹ thừa của biến đó trong B.

+ Nhân các kết quả vừa tìm được với nhau.

Tổng quát: Với a ≠ 0; b ≠ 0, m, n ∈ ℕ, m ≥ n ta có:

(ax^m) : (bxⁿ) = $\frac{\mathrm{a}}{\mathrm{b}}$.(x^m : xⁿ) = $\frac{\mathrm{a}}{\mathrm{b}}$.x^{m – n}

Ví dụ: Tính:

a) 14x² : 7x;

b) 3x⁶ : 2x²;

c) –5yⁿ : 10y² (với n ∈ ℕ, n > 2);

d) (–20x^{m + 1}) : (5x^{n + 1}) (với m, n ∈ ℕ, m > n).

Hướng dẫn giải

a) 14x² : 7x = (14 : 7). (x² : x) = 2x^{2 – 1} = 2x;

b) 3x⁶ : 2x² = $\frac{3}{2}.$x^{6 – 2} = $\frac{3}{2}.$x⁴;

c) Với n ∈ ℕ, n > 2 ta có:

–5yⁿ : 10y² = $\frac{-5}{10}$.y^{n – 2} = $-\frac{1}{2}$y^{n – 2}.

d) Với m, n ∈ ℕ, m > n ta có:

(–20x^{m + 1}) : (5x^{n + 1})

= (–20 : 5). (x^{m + 1} : x^{n + 1})

= –4x^{m + 1 – n – 1} = –4x^{m – n}.

15. Chia đa thức cho đơn thức

Muốn chia đa thức P cho đơn thức Q (Q ≠ 0) khi số mũ của biến ở mỗi đơn thức của P lớn hơn hoặc bằng số mũ của biến đó trong Q, ta chia mỗi đơn thức của đa thức P cho đơn thức Q rồi cộng các thương với nhau.

(A + B) : C = A : C + B : C

(A – B) : C = A : C – B : C

Ví dụ: Tính

a) (20x⁵ – 18x⁴ + 6x² – 4x) : (–2x);

b) (45x⁵ + 10x³ – 5x²) : 5x².

Hướng dẫn giải

a) (20x⁵ – 18x⁴ + 6x² – 4x) : (–2x)

= 20x⁵ : (–2x) – 18x⁴ : (–2x) + 6x² : (–2x) – 4x : (–2x)

= [20 : (–2)](x⁵ : x) – [18 : (–2)](x⁴ : x) + [6 : (–2)](x² : x) – [4 : (–2)](x : x)

= –10x⁴ + 9x³ – 3x + 2.

b) (45x⁵ + 10x³ – 5x²) : 5x²

= 45x⁵ : 5x² + 10x³ : 5x² – 5x² : 5x²

= (45 : 5)(x⁵ : x²) + (10 : 5)(x³ : x²) – (5 : 5)(x² : x²)

= 9x³ + 2x – 1.

16. Chia đa thức một biến đã sắp xếp

* Để chia một đa thức cho một đa thức khác đa thức không (cả hai đa thức đều đã thu gọn và sắp xếp các đơn thức theo số mũ giảm dần của biến) khi bậc của đa thức bị chia lớn hơn hoặc bằng bậc của đa thức chia, ta làm như sau:

– Bước 1.

+ Chia đơn thức bậc cao nhất của đa thức bị chia cho đơn thức bậc cao nhất của đa thức chia.

+ Nhân kết quả trên với đa thức chia và đặt tích dưới đa thức bị chia sao cho hai đơn thức có cùng số mũ của biến ở cùng cột.

+ Lấy đa thức bị chia trừ đi tích đặt dưới để được đa thức mới.

– Bước 2. Tiếp tục quá trình trên cho đến khi nhận được đa thức không hoặc đa thức

có bậc nhỏ hơn bậc của đa thức chia.

* Nhận xét

– Khi chia đa thức A cho đa thức B của cùng một biến (B ≠ 0), có hai khả năng xảy ra:

+ Phép chia có dư bằng 0. Trong trường hợp này ta nói đa thức A chia hết cho đa thức B.

+ Phép chia có dư là đa thức R (R ≠ 0) với bậc của R nhỏ hơn bậc của B. Phép chia trong trường hợp này được gọi là phép chia có dư.

– Người ta chứng minh được rằng đối với hai đa thức tuỳ ý A và B của cùng một biến (B ≠ 0), tồn tại duy nhất một cặp đa thức Q và R sao cho A = B . Q + R, trong đó R bằng 0 hoặc bậc của R nhỏ hơn bậc của B. Như vậy, đã thức A chia hết cho đa thức B khi và chỉ khi R = 0.

Ví dụ: Tính:

a) (9x³ + 6x² + 3x – 3) : (3x + 1)

b) (6x² + 4) : (– 2x – 1)

Hướng dẫn giải

a) Ta thực hiện đặt tính chia đa thức như sau:

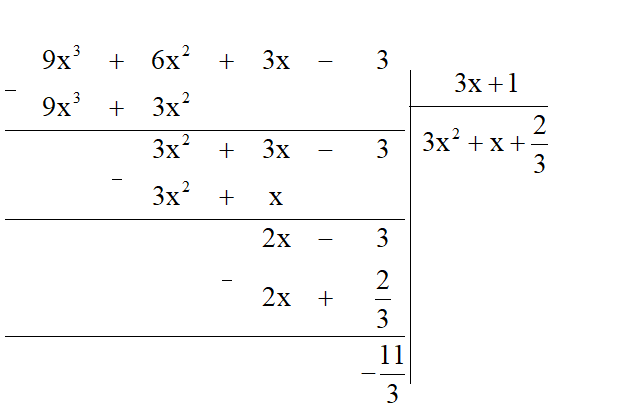
Vậy (9x³ + 6x² + 3x – 3) : (3x + 1) = 3x² + x + $\frac{3}{2}$(dư $\frac{-11}{3}$).

b) Ta thực hiện đặt tính chia đa thức như sau:

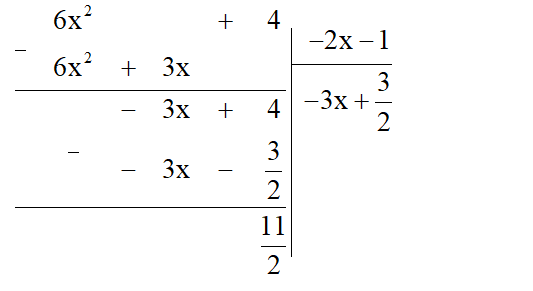
Vậy (6x² + 4) : (–2x – 1) = $-3\text{x}+\frac{3}{2}$ (dư $\frac{11}{2}$).