Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác chi tiết sách Toán 7 Tập 2 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

A. Câu hỏi trong bài

Giải Toán 7 trang 74 Tập 2

Câu hỏi khởi động trang 74 Toán 7 Tập 2: Hình 15 minh hoạ vị trí của ba khu du lịch Yên Tử, Tuần Châu và Vân Đồn (ở tỉnh Quảng Ninh).

 

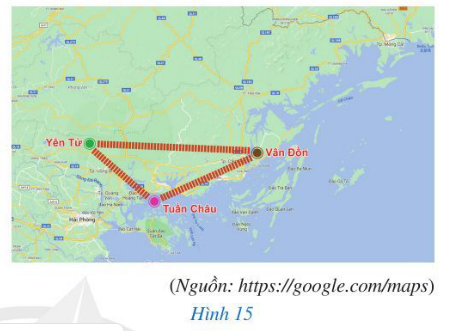
Trong hai vị trí Yên Tử và Tuần Châu, vị trí nào gần Vân Đồn hơn?

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Giả sử ba vị trí Vân Đồn, Yên Tử và Tuần Châu được mô tả bởi các điểm A, B, C như hình vẽ dưới đây:

 

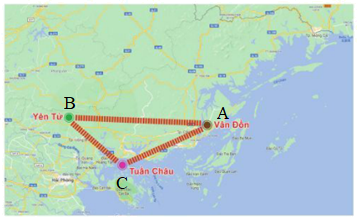
Để biết được trong hai vị trí Yên Tử và Tuần Châu, vị trí nào gần Vân Đồn hơn thì ta đi so sánh độ dài cạnh AB và độ dài cạnh AC.

Xét tam giác ABC ta có góc C là góc tù nên cạnh AB đối diện với góc C là cạnh lớn nhất.

Do đó AB > AC.

Vậy vị trí Tuần Châu gần Vân Đồn hơn.

Hoạt động 1 trang 74 Toán 7 Tập 2: Quan sát tam giác ABC ở Hình 17.

 

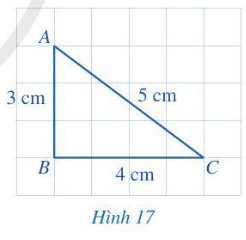
a) So sánh hai cạnh AB và AC.

b) So sánh góc B (đối diện với cạnh AC) và góc C (đối diện với cạnh AB).

Lời giải:

a) Quan sát Hình 17 ta thấy AB = 3 cm, AC = 4 cm.

Vì 3 cm < 4 cm nên AB < AC.

Vậy AB < AC.

b) Tam giác ABC là tam giác vuông tại B nên $\widehat{B}=90°,\widehat{C}$ là góc nhọn nên $\widehat{C}<90°$ 

Do đó $\widehat{B}>\widehat{C}$ 

Vậy $\widehat{B}>\widehat{C}$

Luyện tập 1 trang 74 Toán 7 Tập 2: Cho tam giác MNP có MN = 4 cm, NP = 5 cm, MP = 6 cm. Tìm góc nhỏ nhất, góc lớn nhất của tam giác MNP.

Lời giải:

 

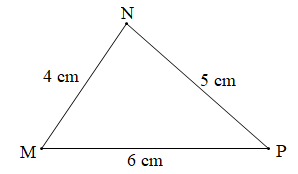
Trong tam giác ABC có MN = 4 cm, NP = 5 cm, MP = 6 cm (giả thiết)

Suy ra MN < NP < MP

Do đó $\widehat{P}<\widehat{M}<\widehat{N}$ 

Vậy trong tam giác MNP thì $\widehat{P}$ là góc nhỏ nhất và $\widehat{N}$ là góc lớn nhất.

Giải Toán 7 trang 75 Tập 2

Hoạt động 2 trang 75 Toán 7 Tập 2: Quan sát tam giác ABC ở Hình 19.

 

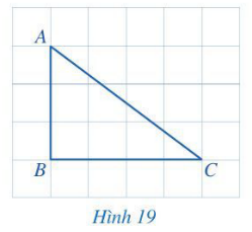
a) So sánh hai góc B và C.

b) So sánh cạnh AB (đối diện với góc C) và cạnh AC (đối diện với góc B).

Lời giải:

a) Quan sát Hình 19 ta thấy tam giác ABC là tam giác vuông tại B nên $\widehat{B}=90°,\widehat{C}$ là góc nhọn nên $\widehat{C}<90°$ 

Do đó $\widehat{B}>\widehat{C}$ 

Vậy $\widehat{B}>\widehat{C}$

b) Quan sát hình vẽ, nếu ta coi độ dài mỗi cạnh hình vuông nhỏ trong hình bằng 1 thì:

+ Độ dài cạnh AB gấp 3 lần độ dài cạnh hình vuông nhỏ nên AB = 3;

+ Độ dài cạnh BC gấp 4 lần độ dài cạnh hình vuông nhỏ nên BC = 4.

Khi đó AB < AC.

Vậy AB < AC.

Luyện tập 2 trang 75 Toán 7 Tập 2: a) Cho tam giác DEG có góc E là góc tù. So sánh DE và DG.

b) Cho tam giác MNP có $\widehat{M}=56°,\widehat{N}=65°.$ Tìm cạnh nhỏ nhất, cạnh lớn nhất của tam giác MNP.

Lời giải:

a)

 

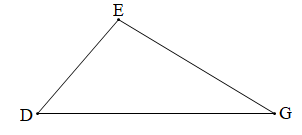
Xét tam giác DEG có góc E là góc tù (giả thiết) nên cạnh DG đối diện với góc E là cạnh lớn nhất.

Do đó DG > DE.

b)

 

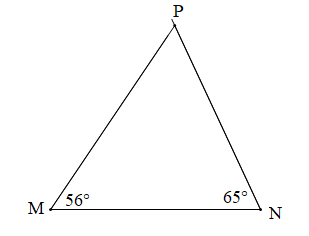
Xét tam giác MNP có $\widehat{M}+\widehat{N}+\widehat{P}=180°$ (tổng ba góc trong một tam giác)

Suy ra $\widehat{P}=180°-\widehat{M}-\widehat{N}$ 

Hay $\widehat{P}=180°-56°-65°=59°$

Ta có: 56° < 59° < 65° hay $\widehat{M}<\widehat{P}<\widehat{N}$ 

Mặt khác: cạnh NP đối diện với góc M, cạnh MP đối diện với góc N, cạnh MN đối diện với góc P.

Suy ra NP < MN < MP

Vậy trong tam giác MNP thì cạnh NP là cạnh nhỏ nhất, cạnh MP là cạnh lớn nhất.

Hoạt động 3 trang 75 Toán 7 Tập 2: Bạn An có hai con đường đi từ nhà đến trường. Đường đi thứ nhất là đường đi thẳng từ nhà đến trường, đường đi thứ hai là đường đi thẳng từ nhà đến hiệu sách rồi đi thẳng từ hiệu sách đến trường (Hình 20). Theo em, bạn An đi từ nhà đến trường theo đường nào sẽ gần hơn?

 

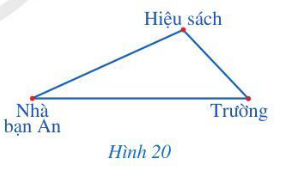
Lời giải

Theo em, bạn An đi từ nhà đến trường theo đường đi thứ nhất (đường thẳng từ nhà đến trường) sẽ gần hơn.

Hoạt động 4 trang 75 Toán 7 Tập 2: Bạn Thảo cho rằng tam giác ABC trong Hình 21 có AB = 3 cm, BC = 2 cm, AC = 4 cm.

 

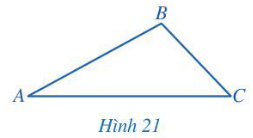
a) Hãy sử dụng thước thẳng (có chia đơn vị) để kiểm tra lại các số đo độ dài ba cạnh của tam giác ABC mà bạn Thảo đã nói.

b) So sánh AB + BC và AC.

Lời giải:

a) Dùng thước thẳng (có chia đơn vị) ta đo được AB = 3cm, BC = 2cm , AC = 4 cm.

Vậy độ dài ba cạnh của tam giác ABC bạn Thảo đã nói đúng.

b) Ta có: AB + BC = 3 + 2 = 5 (cm)

Vì 5 cm > 4 cm nên AB + BC > AC.

Vậy AB + BC > AC.

Giải Toán 7 trang 76 Tập 2

Luyện tập 3 trang 76 Toán 7 Tập 2: Cho tam giác ABC có AB = 2 cm, BC = 4cm. So sánh hai cạnh AC và AB.

Lời giải:

 

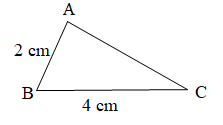
Xét tam giác ABC có: AB = 2 cm, BC = 4 cm (giả thiết)

Theo bất đẳng thức tam giác ta có: AB + AC > BC

Hay 2 + AC > 4 suy ra AC > 4 – 2

Do đó AC > 2 (cm)

Mà AB = 2 cm nên AC > AB.

Vậy AC > AB.

B. Bài tập

Bài 1 trang 76 Toán 7 Tập 2: Cho tam giác MNP có MN = 6 cm, NP = 8 cm, PM = 7 cm. Tìm góc nhỏ nhất, góc lớn nhất của tam giác MNP.

Lời giải:

 

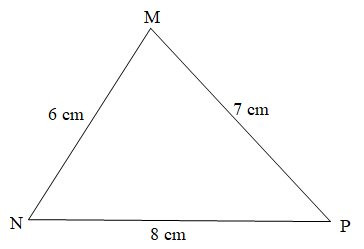
Xét tam giác MNP có MN = 6 cm, NP = 8 cm, PM = 7 cm

Mà 6 cm < 7 cm < 8 cm

Nên MN < MP < NP

Lại có:

+ Cạnh MN đối diện với góc P;

+ Cạnh MP đối diện với góc N;

+ Cạnh NP đối diện với góc M.

Do đó $\widehat{P}<\widehat{N}<\widehat{M}$ 

Vậy trong tam giác MNP thì góc P là góc nhỏ nhất và góc M là góc lớn nhất.

Bài 2 trang 76 Toán 7 Tập 2: Bạn Hoa đi học từ nhà đến trường bằng cách đi xe buýt dọc theo đường Lê Quý Đôn và xuống xe tại một trong hai điểm dừng N hoặc P, rồi từ đó đi bộ đến trường T (Hình 22). Bạn Hoa nên xuống ở điểm dừng nào để quãng đường đi bộ đến trường ngắn hơn?

 

 

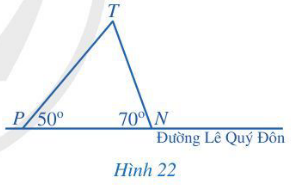
Lời giải:

Ta sẽ so sánh hai quãng đường đi bộ từ điểm dừng N, P đến trường, tức là so sánh NT và PT.

Xét tam giác NPT có:

+ Cạnh NT đối diện với góc P;

+ Cạnh PT đối diện với góc N.

Mà $\widehat{P}<\widehat{N}$ (do 50° < 70°)

Do đó NT < PT.

Vậy bạn Hoa nên xuống ở điểm dừng N để quãng đường đi bộ đến trường ngắn hơn.

Bài 3 trang 76 Toán 7 Tập 2: Theo https://vietnamnet.vn ngày 01/10/2020, sóng 4G có thể phủ đến bán kính 100 km. Người ta đặt một trạm phát sóng 4G tại vị trí A. Có một đảo nhỏ (tại vị trí B) chưa biết khoảng cách đến vị trí A nhưng lại biết khoảng cách từ đảo đó đến một khách sạn (tại vị trí C) là 75 km và khách sạn đó cách vị trí A là 20 km (Hình 23). Sóng 4G của trạm phát sóng tại vị trí A có thể phủ đến đảo đó được không? Vì sao?

 

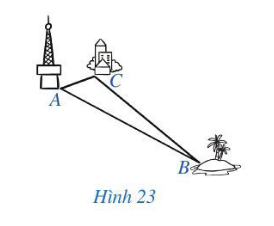
Lời giải:

Quan sát Hình 23 ta có AC = 20 km, BC = 75 km.

Để sóng 4G của trạm phát sóng tại vị trí A có thể phủ đến đảo tại vị trí B thì AB ≤ 100 (km).

Xét tam giác ABC ta có: AC + BC > AB (bất đẳng thức tam giác)

Hay AB < AC + BC

AB < 20 + 75

AB < 95 < 100.

Do đó sóng 4G của trạm phát sóng tại vị trí A có thể phủ đến đảo tại vị trí B.

Giải Toán 7 trang 77 Tập 2

Bài 4 trang 77 Toán 7 Tập 2: Bộ ba số đo độ dài nào trong mỗi trường hợp sau không thể là độ dài ba cạnh của một tam giác?

a) 8 cm, 5 cm, 3 cm;

b) 8 cm, 5 cm, 4 cm;

c) 8 cm, 5 cm, 2 cm.

Lời giải:

Xét các trường hợp:

- Bộ ba số đo độ dài ba cạnh 8 cm, 5 cm, 3 cm:

Ta tính tổng độ dài hai cạnh: 5 + 3 = 8 (cm)

Mà độ dài cạnh còn lại bằng 8 cm

Do đó bộ ba số đo độ dài ba cạnh 8 cm, 5 cm, 3 cm không thể là độ dài ba cạnh của một tam giác.

- Bộ ba số đo độ dài ba cạnh 8 cm, 5 cm, 4 cm:

Ta tính tổng độ dài hai cạnh: 5 + 4 = 9 (cm)

Mà độ dài cạnh còn lại bằng 8 cm và 9 cm > 8 cm

Do đó bộ ba số đo độ dài ba cạnh 8 cm, 5 cm, 4 cm là độ dài ba cạnh của một tam giác.

- Bộ ba số đo độ dài ba cạnh 8 cm, 5 cm, 2 cm:

Ta tính tổng độ dài hai cạnh: 5 + 2 = 7 (cm)

Mà độ dài cạnh còn lại bằng 8 cm và 7 cm < 8 cm

Do đó bộ ba số đo độ dài ba cạnh 8 cm, 5 cm, 2 cm không thể là độ dài ba cạnh của một tam giác.

Vậy trong ba trường hợp thì bộ ba số đo đọ dài của trường hợp a) và c) không thể là độ dài ba cạnh của một tam giác.

Bài 5 trang 77 Toán 7 Tập 2: Con mèo của bạn Huê bị mắc kẹt trên gờ tường cao 4 m. Bác bảo vệ sử dụng một cái thang để đưa mèo xuống giúp bạn Huê. Bác đặt thang dựa vào gờ tường (Hình 24a), khoảng cách từ chân thang đến điểm chạm vào gờ tường là AB = 4,5 m.

 

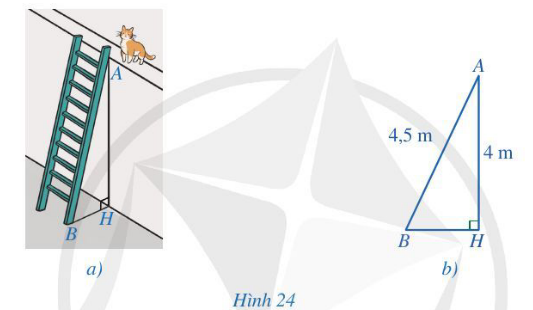
Hình 24b mô tả hình ảnh chiếc thang dựa vào tường trong Hình 24a. Bạn Huê khẳng định chân thang cách chân tường là BH = 0,5 m. Khẳng định của bạn Huê có đúng không? Vì sao?

Lời giải:

Quan sát Hình 24b ta có: AB = 4,5 cm và AH = 4 cm.

Xét tam giác ABH có: BH + AH > AB (bất đẳng thức tam giác)

Suy ra BH > AB – AH

Hay BH > 4,5 – 4

Do đó BH > 0,5 (m)

Vậy khẳng định của bạn Huê là không đúng.

Bài 6 trang 77 Toán 7 Tập 2: Người ta cần làm đường dây điện từ một trong hai trạm biến áp A, B đến trạm biến áp C trên đảo (Hình 25).

 

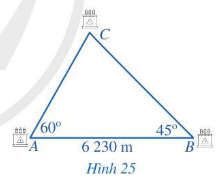
a) Đường dây điện xuất phát từ trạm biến áp nào đến trạm biến áp C sẽ ngắn hơn?

b) Bạn Bình ước lượng: Nếu làm cả hai đường dây điện từ A và từ B đến C thì tổng độ dài đường dây khoảng 6 200 m. Bạn Bình ước lượng có đúng không?

Lời giải:

a) Để xác định được đường dây điện xuất phát từ trạm biến áp nào đến trạm biến áp C ngắn hơn thì ta đi so sánh độ dài hai cạnh AC và BC.

Quan sát Hình 25 ta thấy trong tam giác ABC có $\widehat{A}=60°$ và $\widehat{B}=45°$ 

Do đó $\widehat{A}>\widehat{B}$ (vì 60° > 45°)

Lại có:

+ Cạnh BC đối diện với góc A;

+ Cạnh AC đối diện với góc B.

Suy ra BC > AC.

Vậy đường dây điện xuất phát từ trạm biến áp A đến trạm biến áp C sẽ ngắn hơn đường dây điện xuất phát từ trạm biến áp B đến trạm biến áp C.

Bài 7 trang 77 Toán 7 Tập 2: Cho tam giác ABC có góc A tù. Trên cạnh AC lần lượt lấy các điểm D, E, G sao cho D nằm giữa A và E; E nằm giữa D và G; G nằm giữa E và C (Hình 26).

 

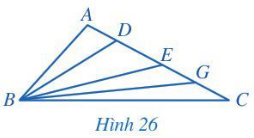
Sắp xếp các đoạn thẳng BA, BD, BE, BG, BC theo thứ tự độ dài tăng dần. Giải thích vì sao.

Lời giải:

- Xét tam giác ABD có góc A là góc tù (giả thiết) nên cạnh BD đối diện với góc A là cạnh lớn nhất.

Do đó BA < BD. (1)

Lại có $\widehat{BDE}$ là góc ngoài của tam giác ABD tại đỉnh D nên ta có: $\widehat{BDE}=\widehat{A}+\widehat{ABD}$ 

Suy ra $\widehat{BDE}>\widehat{A}$

Mà góc A là góc tù nên $\widehat{BDE}$ cũng là góc tù.

- Xét tam giác BDE có $\widehat{BDE}$ cũng là góc tù (chứng minh trên) nên cạnh BE đối diện với $\widehat{BDE}$ là cạnh lớn nhất.

Do đó BD < BE. (2)

Tương tự như trên, ta có:

+ Tam giác BEG có $\widehat{BEG}$ là góc tù nên BG là cạnh lớn nhất hay BE < BG (3)

+ Tam giác BGC có $\widehat{BGC}$ là góc tù nên BC là cạnh lớn nhất hay BG < BC (4)

Từ (1), (2), (3) và (4) ta có: BA < BD < BE < BG < BC.

Vậy sắp xếp các đoạn thẳng trên theo thứ tự độ dài tăng dần là: BA, BD, BE, BG, BC.

Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:

Giải SGK Toán 7 Bài 1: Tổng các góc của một tam giác

Giải SGK Toán 7 Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

Giải SGK Toán 7 Bài 3: Hai tam giác bằng nhau

Giải SGK Toán 7 Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

Giải SGK Toán 7 Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh

Lý thuyết Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

1. Quan hệ giữa góc và cạnh đối diện trong một tam giác

1.1. Góc đối diện với cạnh lớn hơn

– Trong tam giác ABC:

• Góc A được gọi là góc đối diện với cạnh BC;

• Góc B được gọi là góc đối diện với cạnh CA;

• Góc C được gọi là góc đối diện với cạnh AB.

– Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn.

Trong tam giác ABC, nếu AC > AB thì $\widehat{\mathrm{B}}>\widehat{\mathrm{C}}.$

Ví dụ: Cho tam giác ABC có AC = 4 cm, BC = 5 cm. So sánh góc A và góc B.

Hướng dẫn giải

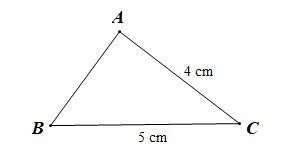
Xét tam giác ABC có BC > AC (5 cm > 4 cm)

Mà $\widehat{\mathrm{A}}$ đối diện với cạnh BC, $\widehat{\mathrm{B}}$ đối diện với cạnh AC.

Nên $\widehat{\mathrm{A}}>\widehat{\mathrm{B}}$ (trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn)

Vậy $\widehat{\mathrm{A}}>\widehat{\mathrm{B}}$.

1.2. Cạnh đối diện với góc lớn hơn

– Trong tam giác ABC:

• Cạnh BC được gọi là cạnh đối diện với góc A;

• Cạnh CA được gọi là cạnh đối diện với góc B;

• Cạnh AB được gọi là cạnh đối diện với góc C.

– Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.

Trong tam giác ABC, nếu $\widehat{\mathrm{B}}>\widehat{\mathrm{C}}$ thì AC > AB.

– Nhận xét:

+ Trong tam giác vuông, cạnh huyền là cạnh lớn nhất.

+ Trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất.

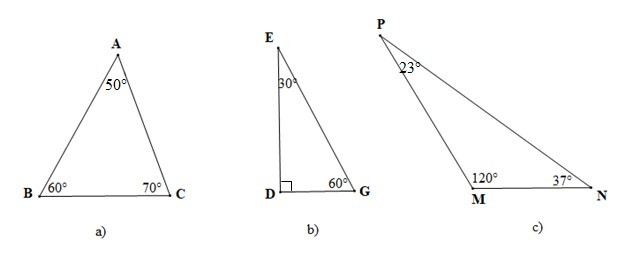
Ví dụ: So sánh các cạnh của tam giác trong các hình vẽ sau:

Hướng dẫn giải

• Hình a)

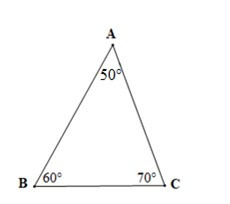
Xét tam giác ABC có $\widehat{\mathrm{C}}>\widehat{\mathrm{B}}>\widehat{\mathrm{A}}$ (70° > 60° > 50°)

Nên AB > AC > BC (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn)

Vậy AB > AC > BC.

• Hình b)

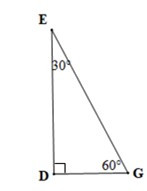
Vì DDEG vuông tại D nên cạnh huyển EG là cạnh lớn nhất (trong tam giác vuông, cạnh huyền là cạnh lớn nhất)

Xét DDEG có $\widehat{\mathrm{G}}>\widehat{\mathrm{E}}$ (60° > 30°)

Nên DE > DG (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn)

Vậy EG > DE > DG.

• Hình c)

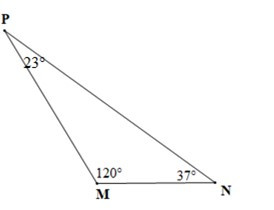
Vì DMNP có $\widehat{\mathrm{M}}=120°$ nên là tam giác tù.

Do đó cạnh NP là cạnh lớn nhất (Trong tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất)

Xét DMNP có $\widehat{\mathrm{N}}>\widehat{\mathrm{P}}$ (37° > 23°)

Nên PM > MN (trong một tam góc, cạnh đối diện với góc lớn hơn là cạnh lớn hơn)

Vậy NP > PM > MN.

2. Bất đẳng thức tam giác

– Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.

Trong tam giác ABC, ta có: AB + BC > AC; AB + AC > BC; AC + BC > AB.

Các bất đảng thức này gọi là các bất đẳng thức tam giác.

– Nhận xét: Trong một tam giác, hiệu độ dài hai cạnh bất kì nhỏ hơn độ dài cạnh còn lại.

Ví dụ: Dựa vào bất đẳng thứ tam giác, kiểm tra xem bộ ba độ dài 2 cm, 8 cm, 6 cm và 3 cm, 5 cm, 7 cm có thể là độ dài ba cạnh của một tam giác không? Vì sao?

Hướng dẫn giải

+) Xét bộ ba độ dài: 2 cm, 8 cm, 6 cm.

Ta có: 2 + 6 = 8 không thỏa mãn bất đẳng thức tam giác nên bộ ba độ dài 2 cm, 8 cm, 6 cm không thể là độ dài ba cạnh của một tam giác.

+) Xét bộ ba độ dài: 3 cm, 5 cm, 7 cm

Ta có: $\left\{\begin{array}{l}3+5=8>7\\ 3+7=10>5\\ 5+7=12>3\end{array}\right.$ thỏa mãn bất đẳng thức tam giác nên bộ ba độ dài 3 cm, 5 cm, 7 cm là độ dài ba cạnh của một tam giác.