Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài 1: Tổng các góc của một tam giác chi tiết sách Toán 7 Tập 2 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:

Giải bài tập Toán lớp 7 Bài 1: Tổng các góc của một tam giác

A. Câu hỏi trong bài

Giải Toán 7 trang 70 Tập 2

Câu hỏi khởi động trang 70 Toán 7 Tập 2: Toà tháp Captial Gate (thuộc Các Tiểu vương quốc A – rập Thống nhất) nghiêng 18° so với phương thẳng đứng (góc nghiêng biểu diễn như Hình 1). Tính đến ngày 01/06/2020, toà tháp này là toà tháp nghiêng nhiều nhất thế giới.

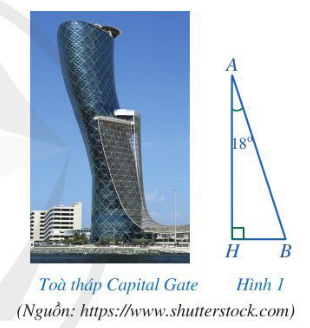
Làm thế nào để biết được độ nghiêng của toà tháp Captial Gate so với phương nằm ngang?

Lời giải:

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Toà tháp Captial Gate được mô tả như Hình 1.

Bài toán trở thành tính số đo góc B.

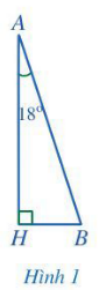
Tam giác ABH vuông tại H nên $\widehat{A}+\widehat{B}=90°$ (tổng hai góc nhọn trong một tam giác vuông).

Suy ra $\widehat{B}=90°-\widehat{A}=90°-18°=72°$ 

Vậy $\widehat{B}=72°$ tức là toà tháp nghiêng một góc 72° so với phương nằm ngang.

Hoạt động 1 trang 70 Toán 7 Tập 2: Cắt tam giác ABC thành ba mảnh (Hình 2a) và ghép lại (Hình 2b). Quan sát Hình 2b và dự đoán tổng ba góc A, B, C.

Lưu ý: Để cho gọn, ta gọi tổng số đo của các góc là tổng các góc đó. Cũng như vậy đối với hiệu hai góc.

Lời giải:

Sau khi cắt tam giác ABC thành ba mảnh (Hình 2a) và ghép lại (Hình 2b) ta dự đoán: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ 

Giải Toán 7 trang 71 Tập 2

Luyện tập 1 trang 71 Toán 7 Tập 2:Cho tam giác đều ABC. Tính số đo mỗi góc của tam giác đó.

Lời giải:

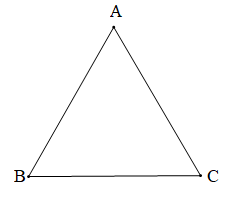
Tam giác ABC là tam giác đều (giả thiết) nên $\widehat{A}=\widehat{B}=\widehat{C}$

Mà $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (tổng ba góc của một tam giác)

Do đó $\widehat{A}+\widehat{A}+\widehat{A}=180°$ 

Hay $3\widehat{A}=180°$ 

Suy ra $\widehat{A}=180°:3=60°$ 

Vậy $\widehat{A}=\widehat{B}=\widehat{C}=60°.$ 

Giải Toán 7 trang 72 Tập 2

Hoạt động 2 trang 72 Toán 7 Tập 2: Cho tam giác ABC vuông tại A. Tổng hai góc B và C bằng bao nhiêu độ?

Lời giải:

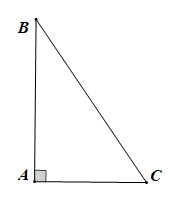
Tam giác ABC vuông tại A (giả thiết) nên $\widehat{A}=90°.$ 

Mà $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (tổng ba góc của một tam giác).

Suy ra $\widehat{B}+\widehat{C}=180°-\widehat{A}=180°-90°=90°.$ 

Vậy .$\widehat{B}+\widehat{C}=90°.$.

Luyện tập 2 trang 72 Toán 7 Tập 2: Trong bài toán nêu ở phần mở đầu, hãy tính độ nghiêng của toà tháp Captial Gate so với phương nằm ngang.

Lời giải:

Toà tháp Captial Gate được mô tả như Hình 1.

Bài toán trở thành tính số đo góc B.

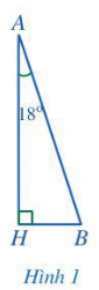
Tam giác ABH vuông tại H nên $\widehat{A}+\widehat{B}=90°$ (tổng hai góc nhọn trong một tam giác vuông).

Suy ra $\widehat{B}=90°-\widehat{A}=90°-18°=72°$ 

Vậy $\widehat{B}=72°$ tức là toà tháp nghiêng một góc 72° so với phương nằm ngang.

B. Bài tập

Bài 1 trang 72 Toán 7 Tập 2: Một khung thép có dạng hình tam giác ABC với số đo các góc ở đỉnh B và đỉnh C cùng bằng 23° (Hình 9). Tính số đo của góc ở đỉnh A.

Lời giải:

Trong tam giác ABC có $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (tổng ba góc của một tam giác).

Suy ra $\widehat{A}=180°-\widehat{B}-\widehat{C}=180°-23°-23°=134°.$

Vậy $\widehat{A}=134°.$ 

Giải Toán 7 trang 73 Tập 2

Bài 2 trang 73 Toán 7 Tập 2: Hình 10 biểu diễn một chiếc cầu trượt gồm máng trượt và thang leo. Tính độ nghiêng của máng trượt so với phương thẳng đứng, biết rằng độ nghiêng của máng trượt so với mặt đất là 38°.

Lời giải:

Chiếc cầu trượt được mô tả như hình vẽ dưới đây:

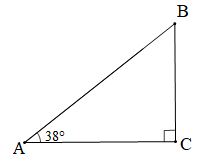
Bài toán trở thành tính số đo góc $\widehat{B}.$ 

Trong tam giác ABC vuông tại C (giả thiết) có $\widehat{A}+\widehat{B}=90°$ (tổng hai góc nhọn trong một tam giác vuông).

Suy ra $\widehat{B}=90°-\widehat{A}=90°-38°=52°.$ 

Vậy máng trượt nghiêng một góc 52° so với phương thẳng đứng.

Bài 3 trang 73 Toán 7 Tập 2: Trong Hình 11, MN // BC. Tính số đo góc C.

Lời giải:

Trong tam giác AMN có $\widehat{A}+\widehat{AMN}+\widehat{ANM}=180°$ (tổng ba góc của một tam giác).

Suy ra $\widehat{ANM}=180°-\widehat{A}-\widehat{AMN}=180°-50°-80°=50°$ 

Mà MN // BC (giả thiết) nên $\widehat{C}=\widehat{ANM}$ (hai góc so le trong)

Suy ra $\widehat{C}=50°.$ 

Vậy $\widehat{C}=50°.$

Bài 4 trang 73 Toán 7 Tập 2: Hình 12 biểu diễn mặt cắt đứng của một đường lên dốc AB.

Để đo độ dốc của con đường biểu diễn bởi góc nhọn BAC tạo bởi đường thẳng AB với phương nằm ngang AC, người ta làm như sau:

- Làm một thước chữ T như Hình 13;

- Đặt thước chữ T dọc theo cạnh AB như Hình 12, $OE\perp AB;$ 

- Buộc một sợi dây vào chân O của thước chữ T và buộc một vật nặng vào đầu dây còn lại, sau đó thả vật nặng để sợi dây có phương thẳng đứng (trong xây dựng gọi là thả dây dọi);

- Tính góc BAC, biết rằng dây dọi OI tạo với trục OE của thước chữ T một góc 15°.

Lời giải:

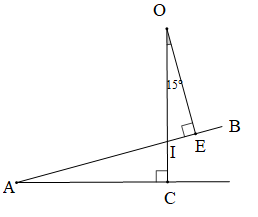
Vì $OE\perp AB$ (giả thiết) nên tam giác OIE vuông tại E do đó ta có: $\widehat{O}+\widehat{OIE}=90°$ (tổng hai góc nhọn trong một tam giác vuông).

Suy ra $\widehat{OIE}=90°-\widehat{O}=90°-15°=75°$ 

Mà $\widehat{AIC}=\widehat{OIE}$ (hai góc đối đỉnh)

Do đó $\widehat{AIC}=75°.$ 

Tam giác AIC vuông tại C nên $\widehat{AIC}+\widehat{IAC}=90°$ (tổng hai góc nhọn trong một tam giác vuông).

Suy ra $\widehat{IAC}=90°-\widehat{AIC}=90°-75°=15°$ 

Hay $\widehat{BAC}=15°.$ 

Vậy $\widehat{BAC}=15°.$

Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:

Giải SGK Toán 7: Bài tập cuối chương 6

Giải SGK Toán 7 Bài 1: Tổng các góc của một tam giác

Giải SGK Toán 7 Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

Giải SGK Toán 7 Bài 3: Hai tam giác bằng nhau

Giải SGK Toán 7 Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

Lý thuyết Tổng ba góc của một tam giác

– Định lí: Tổng ba góc của một tam giác bằng 180°.

Ví dụ 1: Tính số đo của các góc còn lại của mỗi tam giác trong các hình vẽ sau:

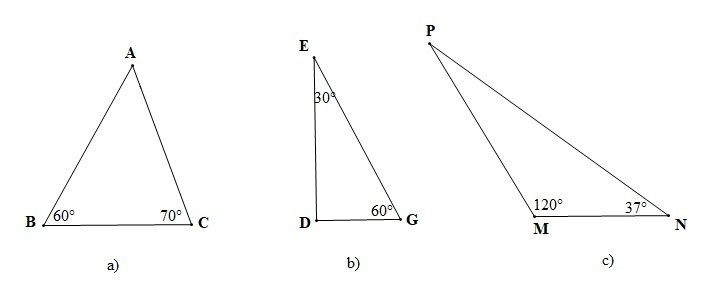
Hướng dẫn giải

• Hình a)

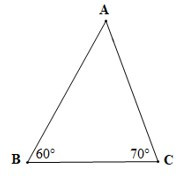
Xét DABC có: $\stackrel{︿}{\text{A}}+\stackrel{︿}{\text{B}}+\stackrel{︿}{\text{C}}=180°$ (định lí tổng ba góc trong một tam giác)

Suy ra $\widehat{\mathrm{A}}=180°-\widehat{\mathrm{C}}-\widehat{\mathrm{B}}$

Mà $\stackrel{︿}{\text{C}}=70°,\stackrel{︿}{\text{B}}=60°$

Do đó $\stackrel{︿}{\text{A}}=180°-70°-60°=50°$

Vậy số đo góc A là 50°.

• Hình b)

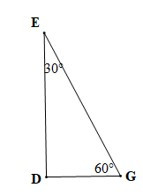
Xét DDEG có $\widehat{\mathrm{D}}+\widehat{\mathrm{E}}+\widehat{\mathrm{G}}=180°$ (định lí tổng ba góc trong một tam giác)

Suy ra $\widehat{\mathrm{D}}=180°-\widehat{\mathrm{E}}-\widehat{\mathrm{G}}$

Mà $\stackrel{︿}{\text{E}}=30°,\stackrel{︿}{\text{G}}=60°$

Do đó $\stackrel{︿}{\text{D}}=180°-30°-60°=90°$

Vậy số đo góc D là 90°.

• Hình c)

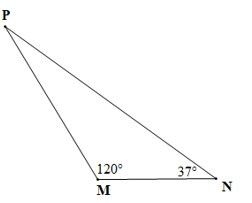
Xét DMNP có: $\stackrel{︿}{\text{M}}+\stackrel{︿}{\text{N}}+\stackrel{︿}{\text{P}}=180°$ (định lí tổng ba góc trong một tam giác)

Suy ra $\widehat{\mathrm{P}}=180°-\widehat{\mathrm{M}}-\widehat{\mathrm{N}}$

Mà $\stackrel{︿}{\text{M}}=120°,\stackrel{︿}{\text{N}}=37°$

Do đó $\stackrel{︿}{\text{P}}=180°-120°-37°=23°$

Vậy số đo góc P là 23°.

– Chú ý:

+ Tam giác có ba góc cùng nhọn gọi là tam giác nhọn.

+ Tam giác có một góc vuông gọi là tam giác vuông.

+ Tam giác có một góc tù gọi là tam giác tù.

Ví dụ 2: Trong Ví dụ 1:

• Tam giác ABC có $\widehat{\mathrm{A}}=50°,\widehat{\mathrm{B}}=60°,\widehat{\mathrm{C}}=70°$ đều là góc nhọn nên là tam giác nhọn.

• Tam giác DEG có $\widehat{\mathrm{D}}=90°$ là góc vuông nên là tam giác vuông tại D.

• Tam giác MNP có $\widehat{\mathrm{M}}=120°$ là góc tù nên là tam giác tù.

- Nhận xét: Trong một tam giác vuông, tổng hai góc nhọn bằng 90°.

Ví dụ 3. Trong Ví dụ 1:

Tam giác DEG là tam giác vuông tại D nên $\widehat{\mathrm{E}}+\widehat{\mathrm{G}}=90°.$

Ví dụ 4. Cho một chiếc thang dựa vào tường. Biết độ nghiêng của chiếc thang đó so với mặt đất là 70°, khi đó độ nghiêng của chiếc thang đó so với bức tường là bao nhiêu?

Hướng dẫn giải

Ta vẽ tam giác vuông ABC (như hình vẽ) để mô tả hình ảnh chiếc thang dựa vào tường.

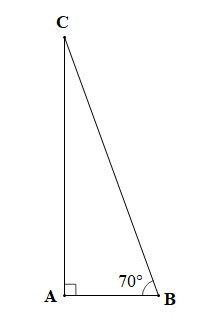
Trong tam giác ABC vuông tại A ta có: $\widehat{\mathrm{B}}+\widehat{\mathrm{C}}=90°$ (trong tam giác vuông, tổng hai góc nhọn bằng 90°)

Suy ra $\widehat{\mathrm{C}}=90°-\widehat{\mathrm{B}}=90°-70°=20°$

Vậy độ nghiêng của chiếc thang so với bức tường là 20°.

– Chú ý: Góc ngoài của tam giác

+ Góc ngoài của một tam giác là góc kề bù với một góc trong của một tam giác đó.

+ Mỗi góc ngoài của một tam giác bằng tổng hai góc trong không kề với nó.

Ví dụ 5. Cho tam giác ABC có $\widehat{\mathrm{B}}=40°,\widehat{\mathrm{C}}=30°.$ Vẽ tia Ax là tia đối của tia AB. Tính số đo góc CAx.

Hướng dẫn giải

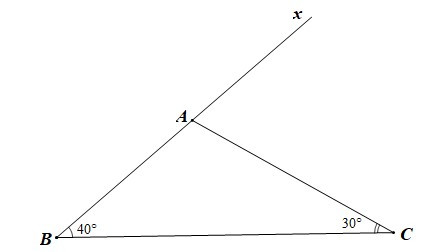
Xét DABC có $\widehat{\text{CAx}}$ là góc ngoài của tam giác tại đỉnh A.

Do đó $\widehat{\mathrm{CAx}}=\widehat{\mathrm{B}}+\widehat{\mathrm{C}}$ (tính chất góc ngoài của tam giác)

Suy ra $\widehat{\mathrm{CAx}}=40°+30°=70°$

Vậy $\widehat{\mathrm{CAx}}=70°.$