Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài tập cuối chương 3 chi tiết sách Toán 10 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài tập cuối chương 3
Video giải Toán 10 Bài tập cuối chương 3 - Cánh diều
Bài 1 trang 60 Toán lớp 10: Tìm tập xác định của mỗi hàm số sau:
a)
b)
c)
Phương pháp giải:
xác định
xác định
xác định
Lời giải:
a) xác định
Tập xác định
b) xác định
Tập xác định
c) xác định
Tập xác định
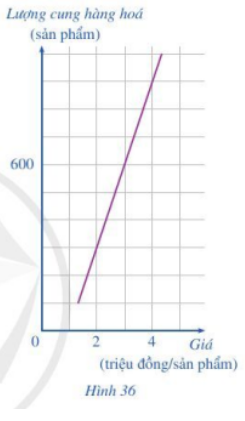
Đồ thị ở Hình 36 cho thấy sự phụ thuộc của lượng hàng hoá được sản xuất (cung) (đơn vị; sản phẩm) bởi giá bán (đơn vị: triệu đồng/sản phẩm) đối với một loại hàng hoá.
a) Xác định lượng hàng hoá được sản xuất khi mức giá bán 1 sản phẩm là 2 triệu đồng; 4 triệu đồng.
b) Biết nhu cầu thị trường đang cần là 600 sản phẩm. Hỏi với mức giá bán là bao nhiêu thì thị trường cân bằng (thị trường cân bằng khi sản lượng cung bằng sản lượng cầu)?
Phương pháp giải:
a) Tìm điểm trên đồ thị có hoành độ bằng 2 và bằng 4. Từ đó tìm tung độ.
b) Tìm điểm trên đồ thị có tung độ bằng 6. Từ đó tìm hoành độ.
Lời giải:
a) Từ đồ thị ta thấy khi giá bán là 2 triệu đồng/sản phẩm thì lượng cung hàng hóa là: 300 sản phẩm, khi giá bán là 4 triệu đồng/sản phẩm thì lượng cung hàng hóa là 900 sản phẩm.
b) Khi nhu cầu thị trường là 600 sản phẩm, để cân bằng thị trường thì lượng cung bằng lượng cầu. Khi đó lượng cung hàng hóa cũng là 600 sản phẩm.
Từ đồ thị ta thấy khi lượng cung hàng hóa là 600 sản phẩm thì giá bán là 3 triệu đồng/sản phẩm.
Gói A: Giá cước 190 000 đồng/tháng.
Nếu trả tiền cước ngày 6 tháng thì sẽ được tặng thêm 1 tháng.
Nếu trả tiền cước ngày 12 tháng thì sẽ được tặng thêm 2 tháng.
Gói B: Giá cước 189 000 đồng/tháng.
Nếu trả tiền cước ngày 7 tháng thì số tiền phải trả cho 7 tháng đó là 1 134 000 đồng.
Nếu trả tiền cước ngày 15 tháng thì số tiền phải trả cho 15 tháng đó là 2 268 000 đồng.
Giả sử số tháng sử dụng Internet là x (1 nguyên dương).
a) Hãy lập các hàm số thể hiện số tiền phải trả ít nhất theo mỗi gói A, B nếu thời gian
dùng không quá 15 tháng.
b) Nếu gia đình bạn Minh dùng 15 tháng thì nên chọn gói nào?
Phương pháp giải:
a) Lập hàm số thể hiện số tiền phải trả theo từng loại gói riêng biệt.
b)
Lời giải:
a) Gói A:
Hàm số:
Gói B:
Hàm số:
b) Gia đình bạn Minh dùng 15 tháng,
+) Nếu chọn gói A: Số tiền phải trả là (đồng)
+) Nếu chọn gói B: Số tiền phải trả là 2268000 đồng.
Vậy gia đình bạn Minh nên chọn gói B.
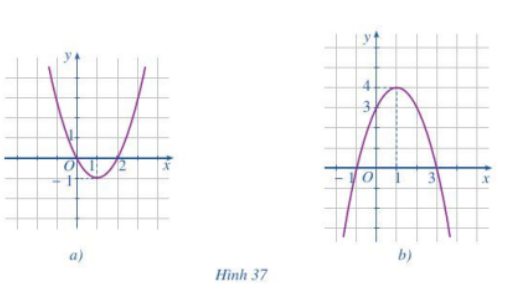
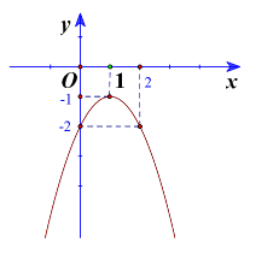
Quan sát đồ thị hàm số bậc hai ở Hình 37a và Hình 37b rồi nêu:
a) Dấu của hệ số a;
b) Toạ độ đỉnh và trục đối xứng;
c) Khoảng đồng biến;
d) Khoảng nghịch biến;
e) Khoảng giá trị x mà y > 0;
g) Khoảng giá trị x mà .
Phương pháp giải:
a) Xác định bề lõm và so sánh a với 0
b) Xác định đỉnh và trục đối xứng của mỗi đồ thị.
c) Quan sát đồ thị và tìm khoảng đồng biến
d) Quan sát đồ thị và tìm khoảng nghịch biến
e) Khoảng giá trị x mà đồ thị nằm trên trục Ox
g) Khoảng giá trị x mà đồ thị nằm dưới trục Ox
Lời giải:
a) Hình 37a: Bề lõm hướng lên trên nên a>0
Hình 37b: Bề lõm xuống nên a<0
b) Hình 37a: Đỉnh là (1;-1), trục đối xứng x=1
Hình 37b: Đỉnh là (1;4), trục đối xứng x=1
c) Hình 37a: Hàm số đồng biến trên
Hình 37b: Hàm số đồng biến trên
d) Hình 37a: Hàm số nghịch biến trên
Hình 37b: Hàm số nghịch biến trên
e) Hình 37a: Đồ thị nằm trên trục Ox khi
=> Khoảng giá trị x mà y > 0 là
Hình 37b: Đồ thị nằm trên trục Ox khi
=> Khoảng giá trị x mà y > 0 là
g) Hình 37a: Đồ thị nằm dưới trục Ox khi
=> Khoảng giá trị x mà y < 0 là
Hình 37b: Đồ thị nằm dưới trục Ox khi
=> Khoảng giá trị x mà là
Bài 5 trang 61 Toán lớp 10: Vẽ đồ thị của mỗi hàm số sau:
a)
b)
c)
Phương pháp giải:
Bước 1: Xác định tọa độ đỉnh
Bước 2: Vẽ trục đối xứng
Bước 3: Xác định một số điểm đặc biệt, chẳng hạn giao điểm với trục tung (0;c) và trục hoành (nếu có), điểm đối xứng với điểm (0;c) qua trục .
Bước 4: Vẽ đường parabol đi qua các điểm đã xác định ta nhận được đồ thị hàm số
Lời giải:
a)
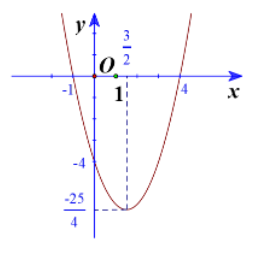
Đồ thị hàm số có đỉnh
Trục đối xứng là
Giao điểm của parabol với trục tung là (0;-4)
Giao điểm của parabol với trục hoành là (-1;0) và (4;0)
Điểm đối xứng với điểm (0;-4) qua trục đối xứng là (3;-4)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
b)
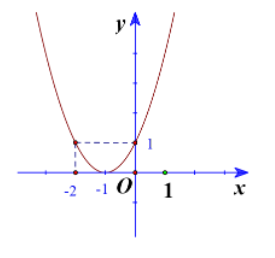
Đồ thị hàm số có đỉnh
Trục đối xứng là
Giao điểm của parabol với trục tung là (0;1)
Giao điểm của parabol với trục hoành là (-1;0)
Điểm đối xứng với điểm (0;1) qua trục đối xứng là (-2;1)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
c)
Đồ thị hàm số có đỉnh
Trục đối xứng là
Giao điểm của parabol với trục tung là (0;-2)
Điểm đối xứng với điểm (0;-2) qua trục đối xứng là (2;-2)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
Bài 6 trang 61 Toán lớp 10: Lập bảng xét dấu của mỗi tam thức bậc hai sau:
a)
b)
c)
Phương pháp giải:
Bước 1: Tìm nghiệm của và hệ số a.
Bước 2: Lập bảng xét dấu.
Lời giải:
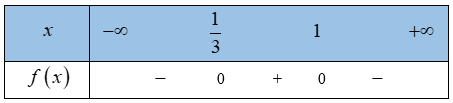
a)
,
=> có 2 nghiệm
Bảng xét dấu:
b)
,
=> có 2 nghiệm
Bảng xét dấu:

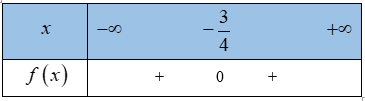
c)
,
=> có nghiệm duy nhất
Bảng xét dấu:
Bài 7 trang 61 Toán lớp 10: Giải các bất phương trình sau:
a)
b)
c)
d)
e)
g)
Phương pháp giải:
Giải bất phương trình dạng .
Bước 1: Xác định dấu của hệ số a và tìm nghiệm của (nếu có)
Bước 2: Sử dụng định lí về dấu của tam thức bậc hai để tìm tập hợp những giá trị của x sao cho mang dấu “+”
Bước 3: Các bất phương trình bậc hai có dạng được giải bằng cách tương tự.
Lời giải:
a)
Tam thức bậc hai có 2 nghiệm phân biệt
hệ số
Ta có bảng xét dấu f(x) như sau:
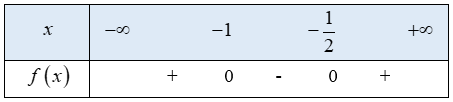
Từ bảng xét dấu ta thấy
Vậy tập nghiệm của bất phương trình là
b)
Tam thức bậc hai có 2 nghiệm phân biệt
Hệ số
Ta có bảng xét dấu f(x) như sau:
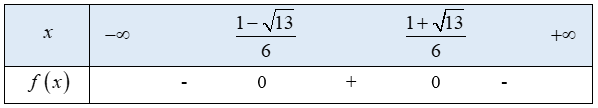
Từ bảng xét dấu ta thấy
Vậy tập nghiệm của bất phương trình là
c)
Tam thức bậc hai có nghiệm duy nhất
hệ số
Ta có bảng xét dấu f(x) như sau:
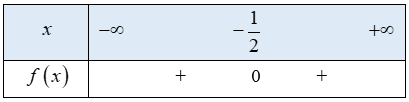
Từ bảng xét dấu ta thấy
Vậy tập nghiệm của bất phương trình là
d)
Tam thức bậc hai có nghiệm duy nhất
hệ số
Ta có bảng xét dấu f(x) như sau:
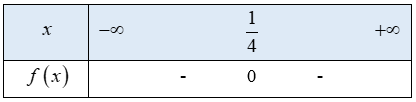
Từ bảng xét dấu ta thấy
Vậy tập nghiệm của bất phương trình là
e)
Ta có và có
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho mang dấu “-” là
Vậy tập nghiệm của bất phương trình là
g)
Tam thức bậc hai có và có
Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho mang dấu “-” là
Vậy tập nghiệm của bất phương trình là
Bài 8 trang 61 Toán lớp 10: Giải các phương trình sau:
a)
b)
c)
Phương pháp giải:
Phương trình dạng
Bước 1: Bình phương hai vế và đưa về phương trình bậc hai một ẩn.
Bước 2: Thay các giá trị tìm được vào bất phương trình . Nghiệm nào thỏa mãn thì giữ lại, không thỏa mãn thì loại.
Bước 3: Kết luận nghiệm
Phương trình có dạng
Bước 1. Giải bất phương trình để tìm tập nghiệm của bất phương trình đó.
Bước 2. Bình phương hai vế của phương trình rồi tìm tập nghiệm.
Bước 3. Trong những nghiệm của phương trình ở bước 2, ta chỉ giữ lại những nghiệm thuộc tập nghiệm của bất phương trình . Tập nghiệm giữ lại đó chính là tập nghiệm của phương trình đã cho.
Lời giải:
a)
Điều kiện:
Bình phương 2 vế của phương trình ta được:
b)
Bình phương 2 vế của phương trình ta được:
Thay vào bất phương trình ta thấy cả 2 nghiệm đều thỏa mãn.
Vậy tập nghiệm là
c)
Điều kiện:
Bình phương 2 vế của phương trình ta được:
Vậy tập nghiệm là
Bài 9 trang 61 Toán lớp 10: Một kĩ sư thiết kế đường dây điện từ vị trí A đến vị trí S và từ vị trí S đến vị trí C trên cù lao như Hình 38. Tiền công thiết kế mỗi ki-lô-mét đường dây từ A đến S và từ S đến C lần lượt là 3 triệu đồng và 5 triệu đồng. Biết tổng số tiền công là 16 triệu đồng. Tính tổng số ki-lô-mét đường dây điện đã thiết kế.
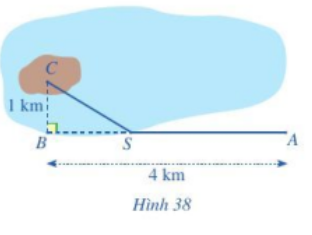
Lời giải:
Gọi khoảng cách từ A đến S là x (km) (0<x<4)
(km)
(km)
Tổng số tiền từ A đến C là:
(triệu đồng)
Khi đó ta có phương trình:
Do
=>
Vậy tổng ki-lô-mét đường dây điện đã thiết kế là SA+SC=3,25+1,25=4,5 (km)
Lý thuyết Toán 10 Chương 3: Hàm số và đồ thị
1. Hàm số
1.1. Định nghĩa
Cho tập hợp khác rỗng D ⊂ ℝ. Nếu với mỗi giá trị của x thuộc D có một và chỉ một giá trị tương ứng của y thuộc tập hợp số thực ℝ thì ta có một hàm số.
Ta gọi x là biến số và y là hàm số của x.
Tập D được gọi là tập xác định của hàm số.
Kí hiệu hàm số: y = f(x), x ∈ D.
1.2. Cách cho hàm số
a) Hàm số cho bằng một công thức
Hàm số được cho bằng biểu thức, cùng cách nói với hàm số cho bằng công thức.
Tập xác định của hàm số y = f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.
b) Hàm số cho bằng nhiều công thức
Một hàm số có thể được cho bằng nhiều công thức.
Ví dụ:
Cho hàm số: f(x) = .
c) Hàm số không cho bằng công thức
Trong thực tiễn, có những tình huống dẫn tới những hàm số không thể cho bằng không thức (hoặc nhiều công thức).
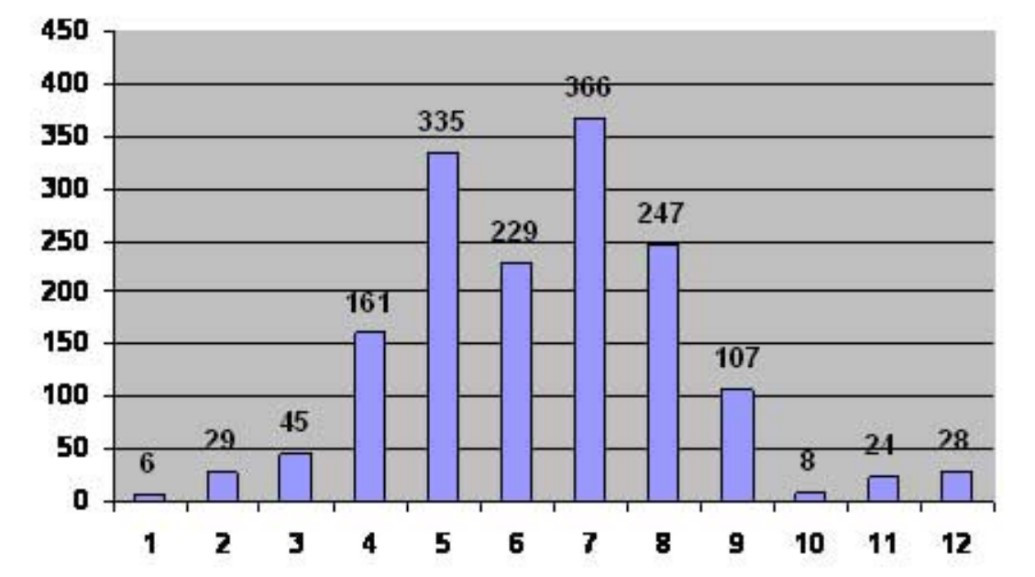
Ví dụ: Biểu đồ lượng mưa tại Hà Nội trong năm 2021 (Đơn vị: mm)
2. Đồ thị của hàm số
Đồ thị của hàm số y = f(x) xác định trên tập hợp D là tập hợp tất cả các điểm
M(x; f(x)) trong mặt phẳng toạ độ Oxy với mọi x thuộc D.
Chú ý:
– Điểm M(a; b) trong mặt phẳng toạ độ Oxy thuộc đồ thị hàm số y = f(x), x ∈ D khi và chỉ khi .
– Để chứng tỏ điểm M(a; b) trong mặt phẳng toạ độ không thuộc đồ thị hàm số
y = f(x), x ∈ D, ta có thể kiểm tra một trong hai khả năng sau:
Khả năng 1: Chứng tỏ rằng a ∉ D
Khả năng 2: Khi a ∈ D thì chứng tỏ rằng b ≠ f(a).
3. Sự biến của hàm số
Cho hàm số y = f(x) xác định trên khoảng (a; b):
– Hàm số y = f(x) gọi là đồng biến trên khoảng (a; b) nếu
– Hàm số y = f(x) gọi là nghịch biến trên khoảng (a; b) nếu
4. Hàm số bậc hai
Hàm số bậc hai là hàm số được cho bằng biểu thức có dạng y = , trong đó a, b, c là những hằng số và a ≠ 0. Tập xác định của hàm số là ℝ.
5. Đồ thị hàm số bậc hai
Đồ thị hàm số bậc hai y = (a ≠ 0) là một đường parabol có đỉnh là điểm với toạ độ và trục đối xứng là đường thẳng .
Các bước vẽ đồ thị hàm số bậc hai
Bước 1: Xác định toạ độ đỉnh: ;
Bước 2: Vẽ trục đối xứng ;
Bước 3: Xác định một số điểm đặc biệt, chẳng hạn: giao điểm với trục tung (có toạ độ (0; c)) và trục hoành (nếu có), điểm đối xứng với điểm có toạ độ (0; c) qua trục đối xứng
Bước 4: Vẽ đường parabol đi qua các điểm đã xác định ta nhận được đồ thị hàm số
– Sự đồng biến nghịch của hàm số bậc hai.
Cho hàm số f(x) = (a ≠ 0)
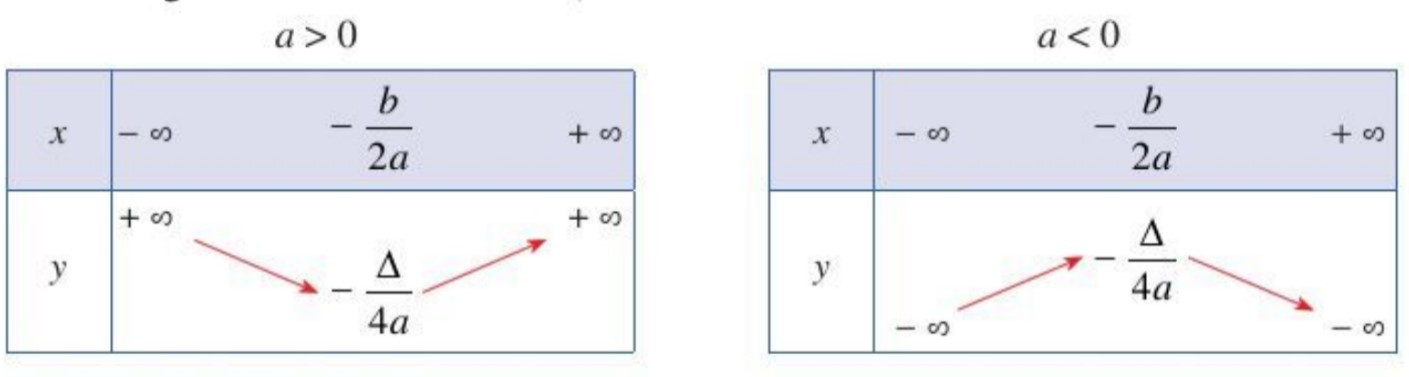
– Nếu a > 0 thì hàm số nghịch biến trên khoảng ; đồng biến trên khoảng
– Nếu a < 0 thì hàm số đồng biến trên khoảng ; nghịch biến trên khoảng
Bảng biến thiên:
6. Dấu của tam thức bậc hai
Cho tam thức bậc hai f(x) = (a ≠ 0), .
+ Nếu ∆ < 0 thì f(x) cùng dấu với hệ số a với mọi x ∈ ℝ
+ Nếu ∆ = 0 thì f(x) cùng dấu với hệ số a với mọi x ∈ ℝ \
+ Nếu ∆ > 0 thì f(x) có hai nghiệm . Khi đó:
– f(x) cùng dấu với hệ số a với mọi x thuộc các khoảng (–∞; ); (; +∞)
– f(x) trái dấu với hệ số a với mọi x thuộc khoảng (; )
7. Bất phương trình bậc hai một ẩn
– Bất phương trình bậc hai một ẩn x là bất phương trình có một trong các dạng sau: ax2 + bx + c < 0; ax2 + bx + c ≤ 0; ax2 + bx + c > 0; ax2 + bx + ≥ 0, trong đó a, b, c là các số thực đã cho, a ≠ 0.
– Đối với bất phương trình bậc hai có dạng ax2 + bx + c < 0, mỗi số sao cho được gọi là một nghiệm của bất phương trình đó.
Tập hợp các nghiệm x như thế còn được gọi là tập nghiệm của bất phương trình bậc hai đã cho.
Nghiệm và tập nghiệm của các dạng bất phương trình bậc hai ẩn x còn lại được định nghĩa tương tự.
8. Giải bất phương trình bậc hai một ẩn
*Cách 1: Xét dấu tam thức bậc hai
f(x) > 0 (f(x) = ax2 + bx + c), ta chuyển việc giải bất phương trình đó về việc tìm tập hợp những giá trị của x sao cho f(x) mang dấu “+”. Cụ thể, ta làm như sau:
Bước 1. Xác định dấu của hệ số a và tìm nghiệm của f(x) (nếu có).
Bước 2. Sử dụng định lí về dấu của tam thức bậc hai để tìm tập hợp những giá trị của x sao cho f(x) mang dấu “+”.
Các bất phương trình bậc hai có dạng f(x) < 0, f(x) ≥ 0, f(x) ≤ 0 được giải bằng cách tương tự.
*Cách 2: Sử dụng hàm số
– Giải bất phương trình bậc hai ax2 +bx + c > 0 là tìm tập hợp những giá trị của x ứng với phần parabol y = ax2 + bx + c nằm phía trên trục hoành.
– Tương tự, giải bất phương trình bậc hai ax2 + bx + c < 0 là tìm tập hợp những giá trị của x ứng với phần parabol y = ax2 + bx + c nằm phía dưới trục hoành.
Như vậy, để giải bất phương trình bậc hai (một ẩn) có dạng:
f(x) > 0 (f(x) = ax2 + bx + c) bằng cách sử dụng đồ thị, ta có thể làm như sau: Dựa vào parabol y = ax2 + bx + c, ta tìm tập hợp những giá trị của x ứng với phần parabol đó nằm phía trên trục hoành. Đối vổi các bất phương trình bậc hai có dạng f(x) < 0, f(x) ≥ 0, ,f(x) ≤ 0, ta cũng làm tương tự.
9. Hai dạng phương trình quy về phương trình bậc hai
* Phương trình có dạng (I)
Để giải phương trình (I) ta làm như sau:
Bước 1: Bình phương hai vế của (I) dẫn đến phương trình f(x) = g(x) rồi tìm nghiệm của phương trình này
Bước 2: Thay từng nghiệm của phương trình f(x) = g(x) vào bất phương trình
f(x) ≥ 0 hoặc g(x) ≥ 0. Nghiệm nào thoả mãn bất phương trình đó thì giữ lại, nghiệm nào không thoả mãn thì loại đi.
Bước 3: Trên cơ sở những nghiệm giữ lại ở Bước 2, ta kết luận nghiệm của phương trình (I)
* Phương trình có dạng (II)
Để giải phương trình (II), ta làm như sau:
Bước 1: Giải bất phương trình g(x) ≥ 0 để tìm tập nghiệm của bất phương trình đó
Bước 2: Bình phương hai vế của phương trình dẫn đến phương trình f(x) = rồi tìm tập nghiệm của phương trình đó.
Bước 3: Trong những nghiệm của phương trình f(x) = , ta chỉ giữ lại những nghiệm thuộc tập nghiệm của bất phương trình g(x) ≥ 0. Tập nghiệm giữ lại đó chính là tập nghiệm của phương trình (II).
Xem thêm các bài giải SGK Toán 10 Cánh diều hay, chi tiết khác:
Bài 5: Hai dạng phương trình quy về phương trình bậc hai
Bài 1: Giá trị lượng giác của một góc từ 0° đến 180°. Định lí côsin và định lí sin trong tam giác
Bài 2: Giải tam giác. Tính diện tích tam giác