Với giải Bài 9 trang 61 Toán lớp 10 Cánh diều chi tiết trong Bài 5: Hai dạng phương trình quy về phương trình bậc hai giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Giải bài tập Toán lớp 10 Bài tập cuối chương III

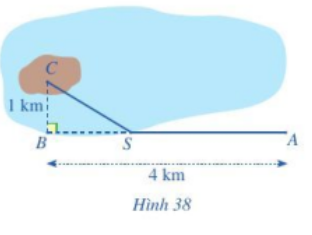
Bài 9 trang 61 Toán lớp 10: Một kĩ sư thiết kế đường dây điện từ vị trí A đến vị trí S và từ vị trí S đến vị trí C trên cù lao như Hình 38. Tiền công thiết kế mỗi ki-lô-mét đường dây từ A đến S và từ S đến C lần lượt là 3 triệu đồng và 5 triệu đồng. Biết tổng số tiền công là 16 triệu đồng. Tính tổng số ki-lô-mét đường dây điện đã thiết kế.

Lời giải:

Gọi khoảng cách từ A đến S là x (km) (0<x<4)

$\Rightarrow BS=4-x$(km)

$\Rightarrow CS=\sqrt{C{B}^2+B{S}^2}$$=\sqrt{1+\left(4-x^2\right)}$(km)

Tổng số tiền từ A đến C là:

$3.SA+5.SC=3.x+5.\sqrt{1+{\left(4-x\right)}^2}$(triệu đồng)

Khi đó ta có phương trình:

$3.x+5.\sqrt{1+{\left(4-x\right)}^2}=16$

$\iff 5\sqrt{1+{\left(4-x\right)}^2}=16-3x$

$\begin{array}{l}25.\left(x^2-8x+17\right)={\left(16-3x\right)}^2\\ \iff 25x^2-200x+425=256-96x+9x^2\\ \iff 16x^2-104x+169=0\\ \iff x=\frac{13}{4}\left(tm\right)\end{array}$

Do $16-3x>0\iff \mathrm{\forall }0<x<4$

=> $SC=\sqrt{1+\left(4-x^2\right)}=1,25$

Vậy tổng ki-lô-mét đường dây điện đã thiết kế là SA+SC=3,25+1,25=4,5 (km)

Bài tập vận dụng:

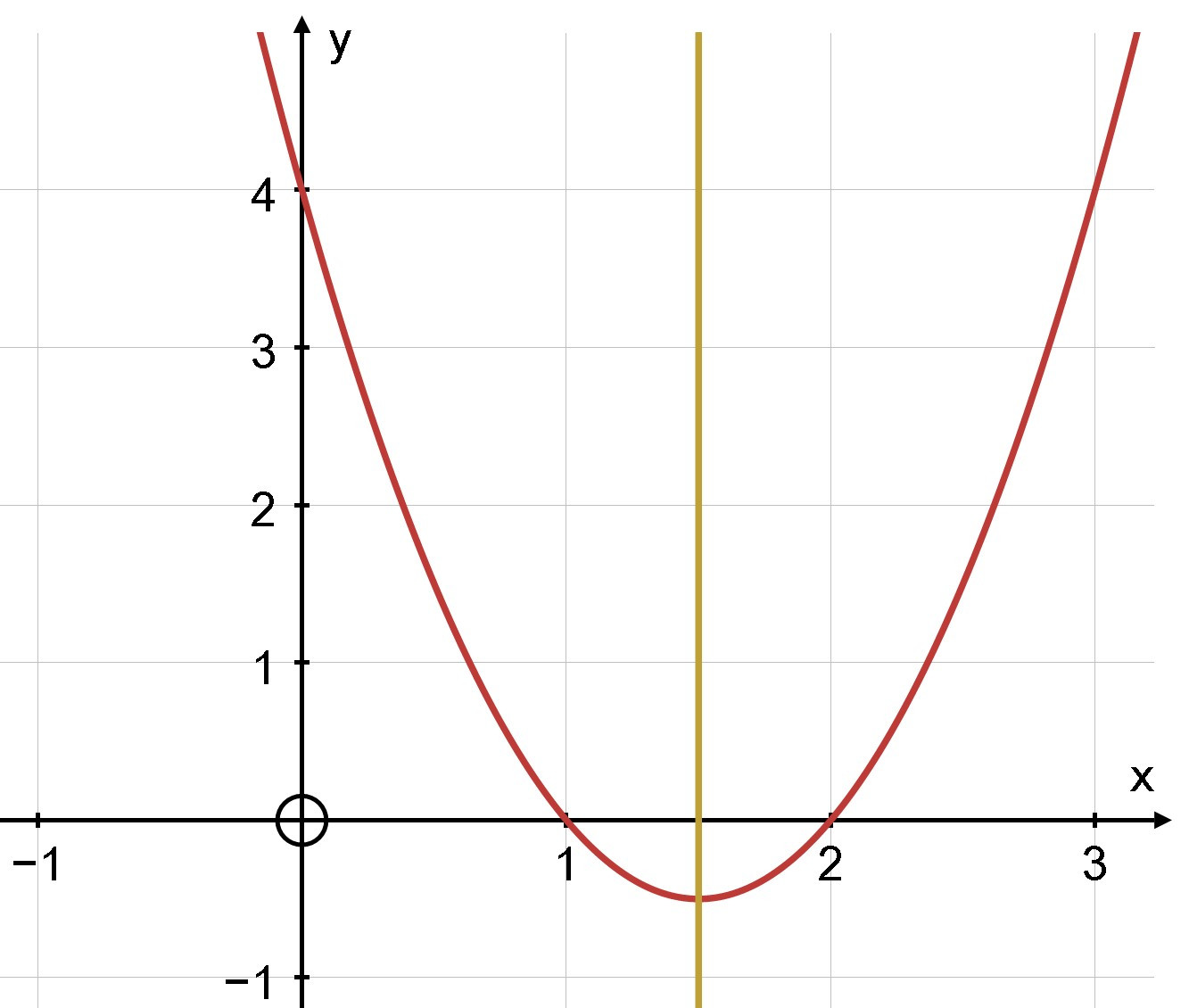
Bài 1. Vẽ đồ thị của hàm số sau: y = 2${\mathrm{x}}^2$ – 6x + 4 

Hướng dẫn giải

– Tập xác định: D = ℝ

– Ta có: a = 2; b = –6; c = 4; $\mathrm{\Delta }={\mathrm{b}}^2-4\text{a}\mathrm{c}$ = ${(-6)}^2$– 4.2.4 = 4

– Toạ độ đỉnh I = $\left(-\frac{\mathrm{b}}{2\text{a}};-\frac{\mathrm{\Delta }}{4\text{a}}\right)$ = $\left(\frac{6}{2.2};\frac{-4}{4.2}\right)=\left(\frac{3}{2};-\frac{1}{2}\right)$

– Trục đối xứng $\mathrm{x}=-\frac{\mathrm{b}}{2\text{a}}$= $\frac{3}{2}$

– Giao điểm của parabol với trục Oy là A(0; 4)

– Giao điểm của parabol với trục Ox là B (1; 0); (2; 0)

– Chọn một điểm thuộc đồ thị cho x = –1 thay vào y = 2${\mathrm{x}}^2$ – 6x + 4 ta được điểm

D(–1; 12)

Vẽ parabol qua các điểm trên:

Bài 2. Khi nào thì tam thức bậc hai $\mathrm{f}\left(\mathrm{x}\right)={\mathrm{x}}^2+\left(\sqrt{5}-1\right)\mathrm{x}-\sqrt{5}$ nhận giá trị dương.

Hướng dẫn giải

Ta có: $\mathrm{f}\left(\mathrm{x}\right)={\mathrm{x}}^2+\left(\sqrt{5}-1\right)\mathrm{x}-\sqrt{5}=0\iff \left[\begin{array}{l}\mathrm{x}=1\\ \mathrm{x}=-\sqrt{5}\end{array}\right.$.

Bảng xét dấu:

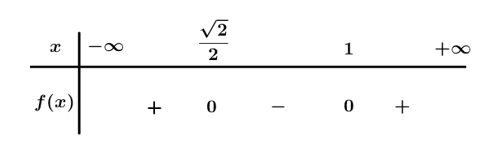
Dựa vào bảng xét dấu $\mathrm{f}\left(\mathrm{x}\right)>0\iff \mathrm{x}\in \left(-\infty ;-\sqrt{5}\right)\cup \left(1;+\infty \right).$ 

Bài 3. Tìm tập nghiệm của bất phương trình: $\sqrt{2}{\mathrm{x}}^2-\left(\sqrt{2}+1\right)\mathrm{x}+1<0$

Hướng dẫn giải

Ta có: $\mathrm{f}\left(\mathrm{x}\right)=\sqrt{2}{\mathrm{x}}^2-\left(\sqrt{2}+1\right)\mathrm{x}+1=0\iff \left[\begin{array}{l}\mathrm{x}=\frac{\sqrt{2}}{2}\\ \mathrm{x}=1\end{array}\right.$.

Bảng xét dấu

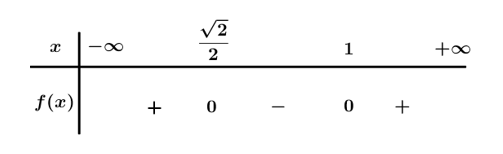
Dựa vào bảng xét dấu $\mathrm{f}\left(\mathrm{x}\right)<0\iff \frac{\sqrt{2}}{2}<\mathrm{x}<1$.

Xem thêm các bài giải Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 1 trang 60 Toán lớp 10: Tìm tập xác định của mỗi hàm số sau:...

Bài 2 trang 60 Toán lớp 10:...

Bài 3 trang 60 Toán lớp 10: Một nhà cung cấp dịch vụ Internet đưa ra hai gói khuyến mại cho người dùng như sau:...

Bài 4 trang 60 Toán lớp 10:...

Bài 5 trang 61 Toán lớp 10: Vẽ đồ thị của mỗi hàm số sau:...

Bài 6 trang 61 Toán lớp 10: Lập bảng xét dấu của mỗi tam thức bậc hai sau:...

Bài 7 trang 61 Toán lớp 10: Giải các bất phương trình sau:...

Bài 8 trang 61 Toán lớp 10: Giải các phương trình sau:...

Xem thêm các bài giải SGK Toán 10 Cánh diều hay, chi tiết khác:

Bài 5: Hai dạng phương trình quy về phương trình bậc hai

Bài tập cuối chương 3

Bài 1: Giá trị lượng giác của một góc từ 0° đến 180°. Định lí côsin và định lí sin trong tam giác

Bài 2: Giải tam giác. Tính diện tích tam giác

Bài 3: Khái niệm vectơ