Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài 5: Hai dạng phương trình quy về phương trình bậc hai chi tiết sách Toán 10 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 5: Hai dạng phương trình quy về phương trình bậc hai
Video giải Toán 10 Bài 5: Hai dạng phương trình quy về phương trình bậc hai - Cánh diều
Câu hỏi khởi động trang 56 Toán lớp 10: Hai ô tô xuất phát tại cùng một thời điểm với vận tốc trung bình như nhua là 40km/h từ hai vị trí A và B trên hai con đường vuông góc với nhau để đi về bến O là giao của hai con đường. Vị trí A cách bên 8km, vị trí B cách bên 7 km. Gọi x là thời gian hai xe bắt đầu chạy cho tới khi cách nhau 5km (Hình 31). Bạn Dương xác định được x thỏa mãn phương trình
Làm thế nào để tìm được giá trị của x?
Phương pháp giải:
Biểu thức dưới căn là số không âm nên ta bình phương hai vế, đưa về phương trình bậc hai.
Lời giải:
Bình phương hai vế ta được:
Vậy phương trình có hai nghiệm là và .
I. Giải phương trình có dạng
Luyện tập vận dụng 1 trang 57 Toán lớp 10: Giải phương trình:
Phương pháp giải:
Bước 1: Bình phương hai vế và đưa về phương trình bậc hai một ẩn.
Bước 2: Thay các giá trị tìm được vào bất phương trình . Nghiệm nào thỏa mãn thì giữ lại, không thỏa mãn thì loại.
Bước 3: Kết luận nghiệm
Lời giải:
Bình phương hai vế ta được:
Thay lần lượt 2 giá trị và vào ta thấy chỉ có thỏa mãn bất phương trình.
Vậy nghiệm của phương trình đã cho là .
II. Giải phương trình có dạng
Luyện tập vận dụng 2 trang 58 Toán lớp 10: Giải phương trình:
Phương pháp giải:
Bước 1. Giải bất phương trình để tìm tập nghiệm của bất phương trình đó.
Bước 2. Bình phương hai vế của phương trình rồi tìm tập nghiệm.
Bước 3. Trong những nghiệm của phương trình ở bước 2, ta chỉ giữ lại những nghiệm thuộc tập nghiệm của bất phương trình . Tập nghiệm giữ lại đó chính là tập nghiệm của phương trình đã cho.
Lời giải:
Bình phương hai vế của phương trình ta được
Vậy tập nghiệm của phương trình đã cho là
Bài tập
Bài 1 trang 58 Toán lớp 10: Giải các phương trình sau:
a)
b)
c)
d)
Phương pháp giải:
Phương trình dạng
Bước 1: Bình phương hai vế và đưa về phương trình bậc hai một ẩn.
Bước 2: Thay các giá trị tìm được vào bất phương trình . Nghiệm nào thỏa mãn thì giữ lại, không thỏa mãn thì loại.
Bước 3: Kết luận nghiệm
Phương trình có dạng
Bước 1. Giải bất phương trình để tìm tập nghiệm của bất phương trình đó.
Bước 2. Bình phương hai vế của phương trình rồi tìm tập nghiệm.
Bước 3. Trong những nghiệm của phương trình ở bước 2, ta chỉ giữ lại những nghiệm thuộc tập nghiệm của bất phương trình . Tập nghiệm giữ lại đó chính là tập nghiệm của phương trình đã cho.
Lời giải:
a) Bình phương hai vế ta được
Thay các giá trị tìm được vào bất phương trình thì thấy cả 2 nghiệm đều thỏa mãn.
Vậy tập nghiệm của phương trình là
b) Bình phương hai vế ta được
Thay các giá trị tìm được vào bất phương trình thì thấy chỉ có nghiệm thỏa mãn.
Vậy tập nghiệm của phương trình là
c) (*)
Ta có:
Bình phương hai vế của (*) ta được:
Vậy tập nghiệm của phương trình là
d) (**)
Ta có:
Bình phương hai vế của (**) ta được:
Vậy tập nghiệm của phương trình là
Bài 2 trang 59 Toán lớp 10: Giải các phương trình sau:
a)
b)
Phương pháp giải:
- Chuyển vế đổi dấu đưa về dạng
- Giải phương trình.
Lời giải:
a) (1)
Ta có:
Bình phương hai vế của (1) ta được:
Vậy tập nghiệm của phương trình là
b) (2)
Ta có:
Bình phương hai vế của (2) ta được:
Vậy tập nghiệm của phương trình là
Bài 3 trang 59 Toán lớp 10: Để leo lên một bức tường, bác Nam dùng một chiếc thang có chiều dài cao hơn bức tường đó 1 m. Ban đầu, bác Nam đặt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng vào mép trên bức tường (Hình 33a). Sau đó, bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 m thì bác Nam nhận thấy thang tạo với mặt đất một góc (Hình 33b). Bức tường cao bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
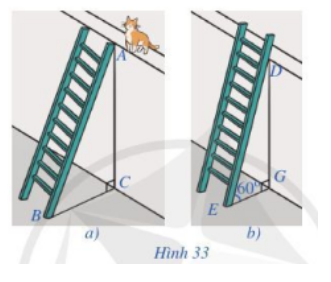
Phương pháp giải:
- Bức tường: AC=DG.
- Vẽ hình ảnh minh họa cho độ dài các cạnh của thang, bức tường.
Lời giải:
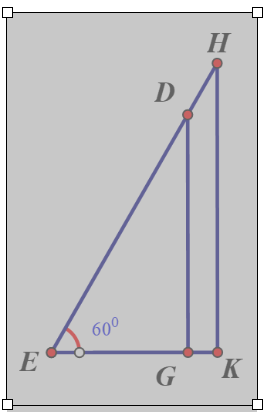
Gọi chiều cao bức tường DG là x (m) (x>0)
Chiều dài chiếc thang là x+1 (m)
Khoảng cách từ chân thang sau khi bác Nam điều chỉnh là: (m)
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
(m)
Bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 m nên ta có:
Ta có (Luôn đúng do x>0)
Ta bình phương hai vế (*) ta được:
Vậy chiều cao của bức tường là 4,7 m.
Bài 4 trang 59 Toán lớp 10: Một người đứng ở điểm A trên một bờ sông rộng 300 m, chèo thuyền đến vị trí D, sau đó chạy bộ đến vị trí B cách C một khoảng 800 m như Hình 34. Vận tốc chèo thuyền là 6 km/h, vận tốc chạy bộ là 10 km/h và giả sử vận tốc dòng nước không đáng kể. Tính khoảng cách từ vị trí C đến D, biết tổng thời gian người đó chèo thuyền và chạy bộ từ A đến B là 7,2 phút.
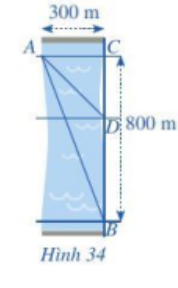
Phương pháp giải:
- Gọi khoảng cách từ C đến D là x m (x>0)
- Biểu diễn DB, AD theo x.
- Biểu diễn đi từ A đến D và đi từ D đến B theo x.
- Lập phương trình và giải.
Lời giải:
Đổi 300 m =0,3 km, 800 m = 0,8 km
7,2 phút =0,12(h)
Gọi khoảng cách từ C đến D là x (km) (0,8>x>0)
Khi đó, DB=0,8-x (km)
Theo định lý Py-ta-go ta có: (km)
Thời gian đi từ A đến D là:
Thời gian đi từ D đến B là:
Tổng thời gian người đó chèo thuyền và chạy bộ từ A đến B là 7,2 phút nên ta có phương trình:
Ta bình phương được do
Vậy khoảng cách từ vị trí C đến D là 414m.
Bài 5 trang 59 Toán lớp 10: Một ngọn hải đăng đặt tại vị trí A cách bờ biển một khoảng cách AB = 4 km. Trên bờ biển có một cái kho ở vị trí C cách B một khoảng là 7 km. Người canh hải đăng có thể chèo thuyền từ A đến vị trí M trên bờ biển với vận tốc 3 km/h rồi đi bộ đến C với vận tốc 5 km/h như Hình 35. Tính khoảng cách từ vị trí B đến M, biết thời gian người đó đi từ A đến C là 148 phút.

Phương pháp giải:
- Gọi BM=x km (0<x<7)
- Biểu diễn MC, AM theo x
- Biểu diễn thời gian từ A đến M và từ M đến C theo x.
- Lập phương trình tìm x.
Lời giải:
Gọi BM=x km (0<x<7)
=> MC=7-x (km)
Ta có:
Thời gian từ A đến M là:
Thời gian từ M đến C là:
Tổng thời gian từ A đến C là 148 phút nên ta có:
Vậy khoảng cách từ vị trí B đến M là 3 km.
Lý thuyết Hai dạng phương trình quy về phương trình bậc hai
I. Giải phương trình có dạng (I)
(f(x) = ax2 + bx + c và g(x) = mx2 + nx + p với a ≠ m)
Để giải phương trình (I) ta làm như sau:
Bước 1: Bình phương hai vế của (I) dẫn đến phương trình f(x) = g(x) rồi tìm nghiệm của phương trình này
Bước 2: Thay từng nghiệm của phương trình f(x) = g(x) vào bất phương trình
f(x) ≥ 0 hoặc g(x) ≥ 0. Nghiệm nào thoả mãn bất phương trình đó thì giữ lại, nghiệm nào không thoả mãn thì loại đi.
Bước 3: Trên cơ sở những nghiệm giữ lại ở Bước 2, ta kết luận nghiệm của phương trình (I)
Chú ý:
– Trong hai bất phương trình f(x) ≥ 0 và g(x) ≥ 0 ta thường chọn bất phương trình dạng đơn giản để thực hiện bước 2.
– Người ta chứng minh được rằng tập hợp (số thực) giữ lại ở Bước 2 chính là tập nghiệm của phương trình (I).
Ví dụ: Giải phương trình (1)
Hướng dẫn giải
Bình phương hai vế của phương trình ta được: = x – 2 (2)
Ta có: (2) ⇔ – 4x + 4 = = 0
Do đó, phương trình (2) có nghiệm là x = 2.
Thay lần giá trị trên vào bất phương trình x – 2 ≥ 0, ta thấy x = 2 thoả mãn bất phương trình
Vậy nghiệm của phương trình (1) là x = 2.
II. Giải phương trình có dạng (II)
(f(x) = a+ bx + c và g(x) = dx + e với a ≠ )
Để giải phương trình (II), ta làm như sau:
Bước 1: Giải bất phương trình g(x) ≥ 0 để tìm tập nghiệm của bất phương trình đó
Bước 2: Bình phương hai vế của phương trình dẫn đến phương trình f(x) = rồi tìm tập nghiệm của phương trình đó.
Bước 3: Trong những nghiệm của phương trình f(x) = , ta chỉ giữ lại những nghiệm thuộc tập nghiệm của bất phương trình g(x) ≥ 0. Tập nghiệm giữ lại đó chính là tập nghiệm của phương trình (II).
Ví dụ: Giải phương trình = x – 1
Hướng dẫn giải
Ta có: x – 1 ≥ 0 ⇔ x ≥ 1
Bình phương hai vế của phương trình, ta được: – 4x + 3 =
⇔ x2 – 4x + 3 = x2 – 2x + 1 ⇔ – 2x + 2 = 0.
Phương trình có hai nghiệm là x = 1, giá trị x = 1 là thoả mãn x ≥ 1
Vậy phương trình có nghiệm là x = 1.
Bài giảng Toán 10 Bài 5: Hai dạng phương trình quy về phương trình bậc hai - Cánh diều
Xem thêm các bài giải SGK Toán 10 Cánh diều hay, chi tiết khác:
Bài 4: Bất phương trình bậc hai một ẩn
Bài 1: Giá trị lượng giác của một góc từ 0° đến 180°. Định lí côsin và định lí sin trong tam giác