Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng chi tiết sách Toán 10 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10. Mời các bạn đón xem:
Giải bài tập Toán lớp 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai
Video giải Toán 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai - Cánh diều
Câu hỏi khởi động trang 39 Toán lớp 10: Cầu cảng Sydney là một trong những hình ảnh biểu tượng của thành phố Sydney và nước Australia. Độ cao y(m) của một điểm thuộc vòng cung thành cầu cảng Sydney có thể biểu thị theo độ dài x(m) tính từ chân cầu bên trái dọc theo đường nối với chân cầu bên phải như sau (Hình 10):

Hàm số có gì đặc biệt?
Lời giải:
Hàm số có đồ thị là một hình parabol, bề lõm quay xuống dưới.
Hình ảnh hình học có tính đối xứng.
I. Hàm số bậc hai
Hoạt động 1 trang 39 Toán lớp 10: Cho hàm số .
a) Viết công thức xác định hàm số trên về dạng đa thức theo lũy thừa với số mũ giảm dần của x.
b) Bậc của đa thức trên bằng bao nhiêu?
c) Xác định hệ số của , hệ số của x và hệ số tự do.
Phương pháp giải:
a) Phá ngoặc và thu gọn.
b) Tìm số mũ cao nhất.
c) Tìm hệ số gắn với , x và hệ số tự do.
Lời giải:
a) Ta có:
b) Bậc của đa thức là 2
c) Hệ số của là -0,00188
Hệ số của x là 0,94564
Hệ số tự do là -0,91423
Luyện tập vận dụng 1 trang 39 Toán lớp 10: Cho hai ví dụ về hàm số bậc hai.
Phương pháp giải:
Hàm số bậc hai: trong đó a,b,c là hằng số và
Lời giải:
Ví dụ 1:
Ví dụ 2:
II. Đồ thị hàm số bậc hai
Hoạt động 2 trang 39 Toán lớp 10: Cho hàm số .
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:
|
x |
-3 |
-2 |
-1 |
0 |
1 |
|
y |
? |
? |
? |
? |
? |
b) Vẽ các điểm của đồ thị hàm số trong mặt phẳng tọa độ Oxy.
c) Vẽ đường cong đi qua 5 điểm A, B, C, D, E. Đường cong đó là đường parabol và cũng chính là đồ thị hàm số (Hình 11).
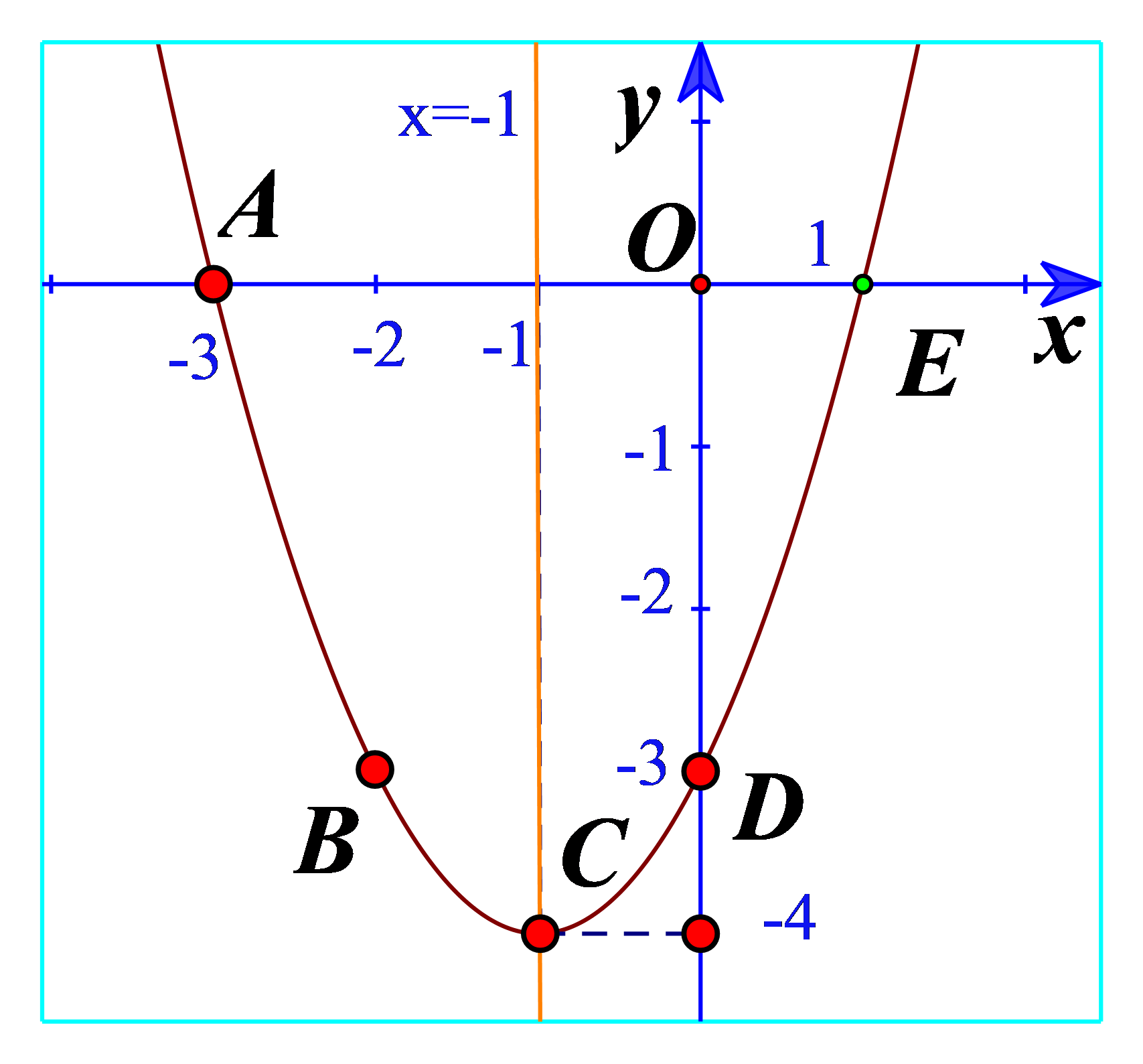
d) Cho biết tọa độ của điểm thấp nhất và phương trình trục đối xứng của parabol đó. Đồ thị hàm số đó quay bề lõm lên trên hay xuống dưới?
Phương pháp giải:
a) Thay vào hàm số.
b) Xác định các điểm trên mặt phẳng.
c) Sử dụng thước hoặc công cụ khác để vẽ đồ thị nối 5 điểm.
d) Tìm điểm thấp nhất trên hình vẽ và đường thẳng x=a với a là hoành độ của điểm thấp nhất.
Lời giải:
a) Thay vào hàm số ta được:
. Điền 0 vào ô tương ứng.
Thay vào hàm số ta được:
. Điền vào ô tương ứng.
Thay vào hàm số ta được:
. Điền vào ô tương ứng.
Thay vào hàm số ta được:
. Điền vào ô tương ứng.
Thay vào hàm số ta được:
. Điền 0 vào ô tương ứng.
Vậy ta có:
|
x |
-3 |
-2 |
-1 |
0 |
1 |
|
y |
0 |
-3 |
-4 |
-3 |
0 |
b) Các điểm có trong hình 11.
c) Đường cong đi qua 5 điểm là parabol trong hình 11.
d) Từ đồ thị ta thấy điểm thấp nhất là điểm C(-4;-1)
Phương trình trục đối xứng là x=-1
Đồ thị có bề lõm lên trên.
Hoạt động 3 trang 40 Toán lớp 10: Cho hàm số .
a) Tìm tọa độ 5 điểm thuộc đồ thị hàm số trên có hoành độ lần lượt là rồi vẽ chúng trong mặt phẳng tọa độ Oxy.
b) Vẽ đường cong đi qua 5 điểm trên. Đường cong đó cũng là đường parabol và là đồ thị của hàm số (Hình 12).
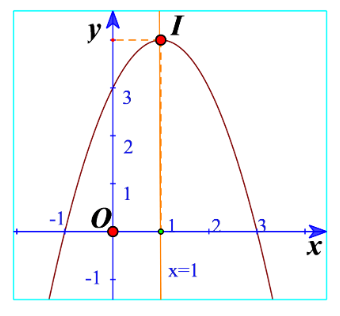
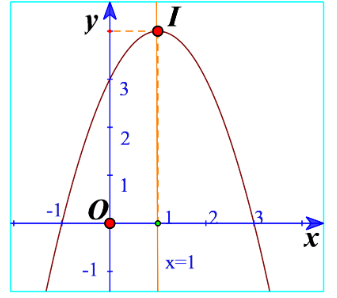
c) Cho biết tọa độ của điểm cao nhất và phương trình trục đối xứng của parabol đó. Đồ thị hàm số đó quay bề lõm lên trên hay xuống dưới?
Phương pháp giải:
a) Từ các điểm trên Ox có hoành độ lần lượt là , kẻ các đường thẳng song song với Oy, xác định giao điểm với đồ thị rồi tìm tung độ của các điểm đó.
b) Vẽ đường cong đi qua 5 điểm trên.
c) Tìm tọa độ của điểm cao nhất và phương trình trục đối xứng của parabol. Xác định bề lõm.
Lời giải:
a) Từ các điểm trên Ox có hoành độ lần lượt là , kẻ các đường thẳng song song với Oy, giao điểm với độ thị lần lượt là: A, B, I, C, D
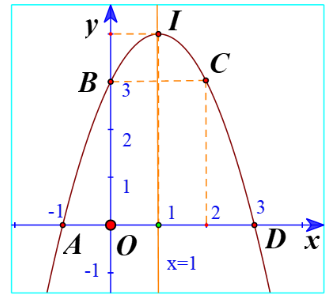
b) Vẽ đồ thị:
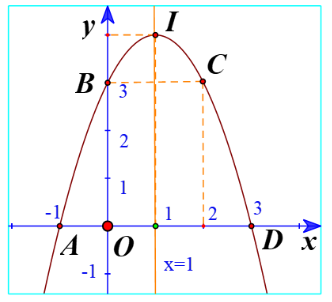
c) Điểm cao nhất là điểm I(1;4)
Phương trình trục đối xứng là đường thẳng x=1.
Đồ thị hàm số đó quay bề lõm xuống dưới.
Luyện tập vận dụng 2 trang 41 Toán lớp 10: Vẽ đồ thị mỗi hàm số bậc hai sau:
a)
b)
c)
Phương pháp giải:
Bước 1: Xác định tọa độ đỉnh
Bước 2: Vẽ trục đối xứng
Bước 3: Xác định một số điểm đặc biệt, chẳng hạn giao điểm với trục tung (0;c) và trục hoành (nếu có), điểm đối xứng với điểm (0;c) qua trục .
Bước 4: Vẽ đường parabol đi qua các điểm đã xác định ta nhận được đồ thị hàm số .
Lời giải:
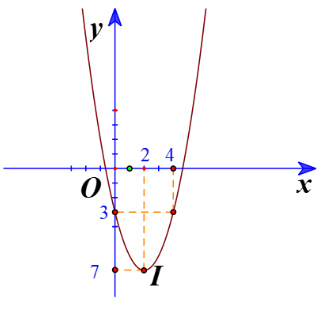
a) Đồ thị hàm số có đỉnh
Trục đối xứng là x=2
Giao điểm của parabol với trục tung là (0;-3)
Điểm đối xứng với điểm (0;-3) qua trục đối xứng x=2 là (4;3)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
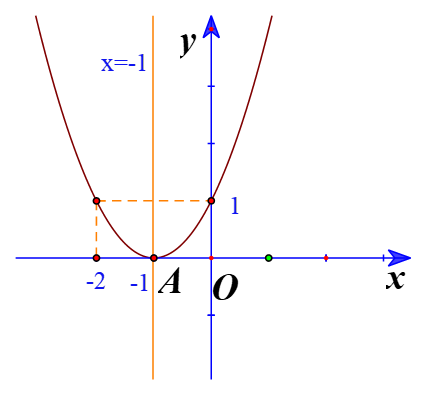
b) Đồ thị hàm số có đỉnh
Trục đối xứng là x=-1
Giao điểm của parabol với trục tung là (0;1)
Giao điểm của parabol với trục hoành là (-1;0)
Điểm đối xứng với điểm (0;1) qua trục đối xứng x=-1 là (-2;1)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
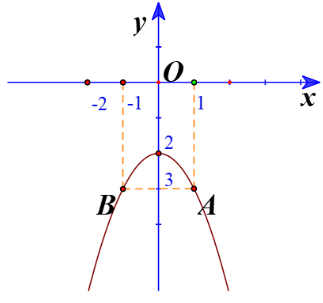
c) Đồ thị hàm số có đỉnh
Trục đối xứng là x=0
Giao điểm của parabol với trục tung là (0;-2)
Cho x=1=>y=-3
=> Điểm A(1;-3) thuộc đồ thị.
Điểm đối xứng với A qua trục đối xứng x=0 là điểm B(-1;-3).
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
Hoạt động 4 trang 41 Toán lớp 10: a) Quan sát đồ thị hàm số bậc hai trong Hình 11. Xác định khoảng đồng biến, khoảng nghịch biến của hàm số và lập bảng biến thiên của hàm số đó.
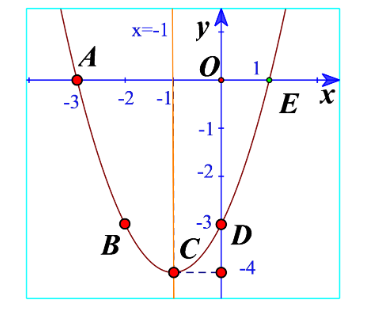
b) Quan sát đồ thị hàm số bậc hai trong Hình 12. Xác định khoảng đồng biến, khoảng nghịch biến của hàm số và lập bảng biến thiên của hàm số đó.
Phương pháp giải:
- Khoảng đồng biến: Khoảng mà đồ thị đi lên.
- Khoảng nghịch biến: Khoảng mà đồ thị đi xuống.
- Lập bảng biến thiên.
Lời giải:
a) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng nên hàm số đồng biến trong khoảng . Trong khoảng thì hàm số nghich biến.
Bảng biến thiên:
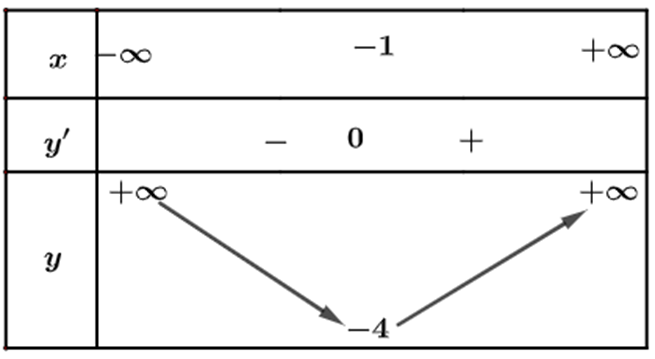
b) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng nên hàm số đồng biến trong khoảng . Trong khoảng thì hàm số nghịch biến.
Bảng biến thiên:
Luyện tập vận dụng 3 trang 42 Toán lớp 10: Lập bảng biến thiên của mỗi hàm số sau:
a)
b)
Phương pháp giải:
- Xác định hệ số a, b.
- Tính .
- Tìm khoảng đồng biến, nghịch biến.
Lời giải:
a) Hệ số
Vậy hàm số nghịch biến trên khoảng và đồng biến trên
b) Ta có
Vậy hàm số đã cho đồng biến trên khoảng và nghịch biến trên khoảng
III. Ứng dụng

Phương pháp giải:
Độ cao y là tung độ của đỉnh parabol.
Lời giải:
Hàm số biểu diễn đồ thị
Khi đó độ cao y (m) của một điểm thuộc vòng cung thành cầu cảng Sydney đạt giá trị lớn nhất là
Bài tập
Bài 1 trang 43 Toán lớp 10: Trong các hàm số sau, hàm số nào là hàm số bậc hai? Với những hàm số bậc hai đó, xác định lần lượt là hệ số của , hệ số của và hệ số tự do.
a)
b)
c)
Phương pháp giải:
- Xác định hàm số bậc hai (số mũ cao nhất là 2)
- Tìm hệ số a, b, c.
Lời giải:
a) Hàm số là hàm số bậc hai.
Hệ số .
b) Hàm số có số mũ cao nhất là 3 nên không là hàm số bậc hai.
c) Hàm số có số mũ cao nhất là 2 nên là hàm số bậc hai.
Hệ số
Bài 2 trang 43 Toán lớp 10: Xác định parabol trong mỗi trường hợp sau:
a) Đi qua điểm và
b) Có đỉnh là
Lời giải:
a) Thay tọa độ điểm và ta được:
Vậy parabol là
b) Hoành độ đỉnh của parabol là
Nên ta có: (1)
Thay tọa độ điểm I vào ta được:
Từ (1) và (2) ta được hệ
Vậy parabol là .
Bài 3 trang 43 Toán lớp 10: Vẽ đồ thị của mỗi hàm số sau:
a)
b)
Phương pháp giải:
Bước 1: Xác định tọa độ đỉnh
Bước 2: Vẽ trục đối xứng
Bước 3: Xác định một số điểm đặc biệt, chẳng hạn giao điểm với trục tung (0;c) và trục hoành (nếu có), điểm đối xứng với điểm (0;c) qua trục .
Bước 4: Vẽ đường parabol đi qua các điểm đã xác định ta nhận được đồ thị hàm số .
Lời giải:
a) Đồ thị hàm số có đỉnh
Trục đối xứng là
Giao điểm của parabol với trục tung là (0;4)
Giao điểm của parabol với trục hoành là (2;0) và (1;0)
Điểm đối xứng với điểm (0;4) qua trục đối xứng là
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
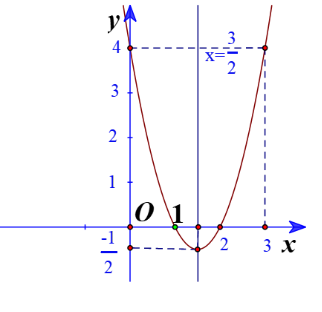
b) Đồ thị hàm số có đỉnh
Trục đối xứng là
Giao điểm của parabol với trục tung là (0;-3)
Giao điểm của parabol với trục hoành là
Điểm đối xứng với điểm (0;-3) qua trục đối xứng là (-2;-3)
Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
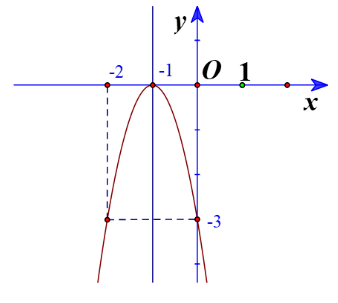
Bài 4 trang 43 Toán lớp 10: Cho đồ thị hàm số bậc hai ở Hình 15.
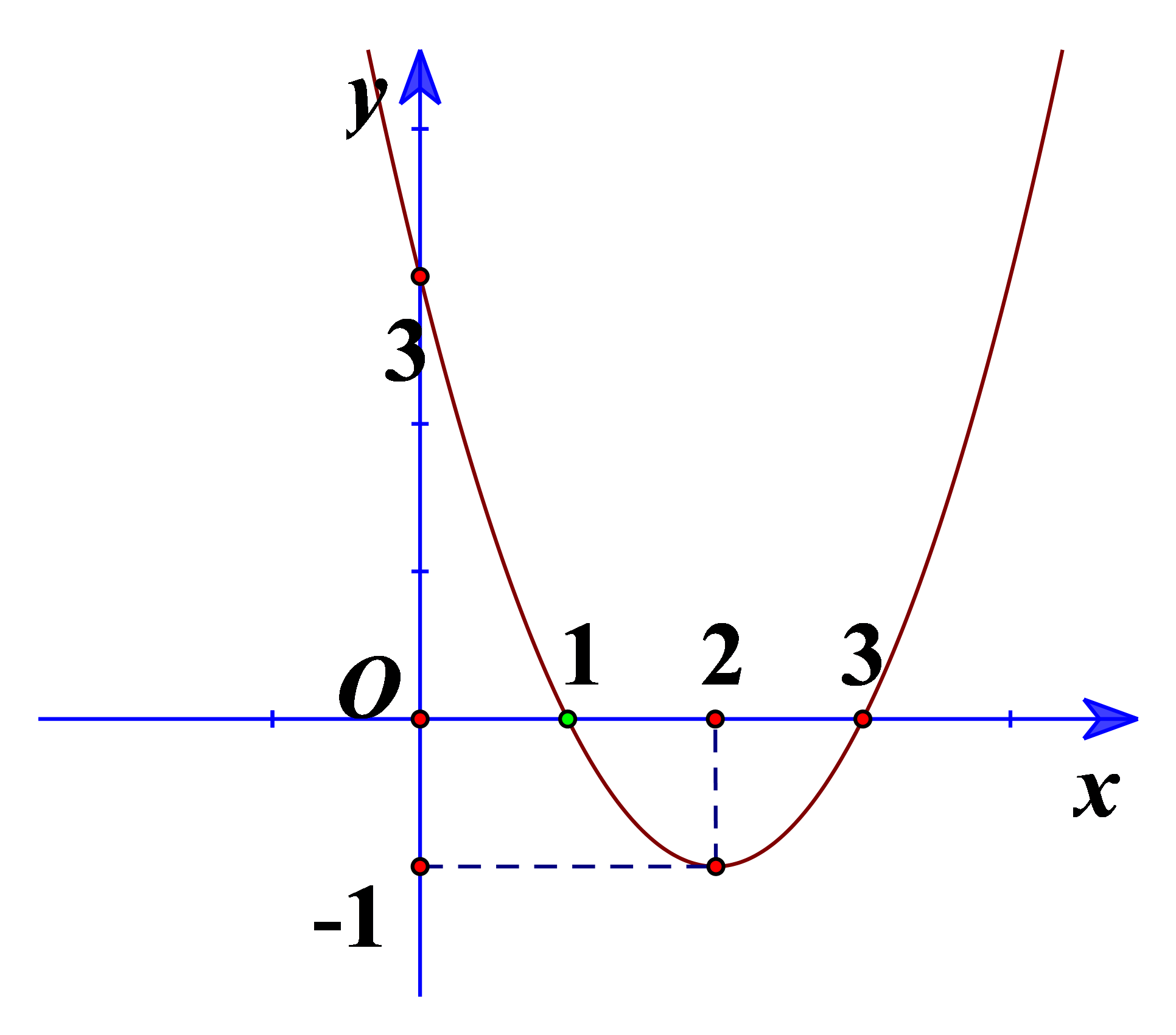
a) Xác định trục đối xứng, tọa độ đỉnh của đồ thị hàm số.
b) Xác định khoảng đồng biến, khoảng nghịch biến của hàm số.
c) Tìm công thức xác định hàm số.
Phương pháp giải:
a) Tìm trục đối xứng trên đồ thị, đỉnh I trên đồ thị.
b) Đồ thị đi lên thì hàm số đồng biến, đi xuống thì hàm số nghịch biến.
c) Gọi hàm số là
Đồ thị hàm số có đỉnh là , xác định thêm 1 điểm thuộc đồ thị và thay vào phương trình tìm a, b, c.
Lời giải:
a) Trục đối xứng là đường thẳng
Đỉnh là
b) Từ đồ thị ta thấy trên khoảng thì hàm số đi xuống nên hàm số nghịch biến trên .
Trên khoảng thì hàm số đi xuống nên đồng biến trên .
c) ) Gọi hàm số là
Đồ thị hàm số có đỉnh là nên ta có:
Ta lại có điểm thuộc đồ thị nên ta có:
Vậy ta có hệ sau:
Vậy parabol là
Bài 5 trang 43 Toán lớp 10: Nêu khoảng đồng biến, khoảng nghịch biến của mỗi hàm số sau:
a)
b)
Phương pháp giải:
- Xác định hệ số a, b.
- Tính .
- Tìm khoảng đồng biến, nghịch biến.
Lời giải:
a) Hệ số
Vậy hàm số nghịch biến trên khoảng và đồng biến trên
b) Ta có
Vậy hàm số đã cho đồng biến trên khoảng và nghịch biến trên khoảng
Bài 6 trang 43 Toán lớp 10: Khi du lịch đến thành phố St. Louis (Mỹ), ta sẽ thấy một cái cổng lớn có hình parabol hướng bề lõm xuống dưới, đó là cổng Arch. Giả sử ta lập một hệ toạ độ Oxy sao cho một chân cổng đi qua gốc O như Hình 16 (x và y tính bằng mét), chân kia của cổng ở vị trí có toạ độ (162;0). Biết một điểm M trên cổng có toạ độ là (10;43). Tính chiều cao của cổng (tính từ điểm cao nhất trên cổng xuống mặt đất), làm tròn kết quả đến hàng đơn vị.
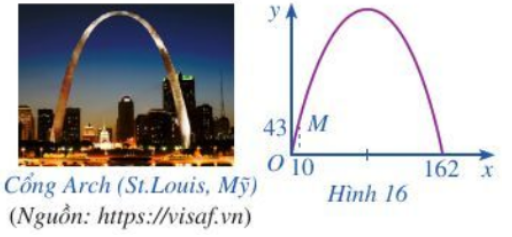
Phương pháp giải:
- Xác định các điểm thuộc đồ thị.
- Gọi hàm số là
- Thay tọa độ các điểm vào và tìm a, b, c.
- Tìm đỉnh của parabol, từ đó suy ra chiều cao của cổng.
Lời giải:
Từ đồ thị ta thấy các điểm thuộc đồ thị là: .
Gọi hàm số là
Thay tọa độ các điểm A, B, C vào ta được hệ:
Từ đố ta có
Hoành độ đỉnh của đồ thị là:
Khi đó: (m)
Vậy chiều cao của cổng là 186m.
Lý thuyết Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng
1. Hàm số bậc hai
Hàm số bậc hai là hàm số được cho bằng biểu thức có dạng y = , trong đó a, b, c là những hằng số và a ≠ 0. Tập xác định của hàm số là ℝ.
Ví dụ:
– Hàm số y = là hàm số bậc hai có hệ số của x2 bằng 2, hệ số của x bằng 3 và hệ số tự do bằng –2.
– Hàm số y = 2x – 3 không phải là hàm số bậc số do hệ số của x2 ở đây bằng 0.
2. Đồ thị hàm số bậc hai
Đồ thị hàm số bậc hai y = (a ≠ 0) là một đường parabol có đỉnh là điểm với toạ độ và trục đối xứng là đường thẳng .
Chú ý: Cho hàm số f(x) = (a ≠ 0), ta có: = f
Để vẽ đồ thị hàm số y = (a ≠ 0) ta thực hiện các bước:
Bước 1: Xác định toạ độ đỉnh: ;
Bước 2: Vẽ trục đối xứng ;
Bước 3: Xác định một số điểm đặc biệt, chẳng hạn: giao điểm với trục tung (có toạ độ (0; c)) và trục hoành (nếu có), điểm đối xứng với điểm có toạ độ (0; c) qua trục đối xứng
Bước 4: Vẽ đường parabol đi qua các điểm đã xác định ta nhận được đồ thị hàm số.
Ví dụ: Vẽ đồ thị hàm số bậc hai y =
Hướng dẫn giải
– Tập xác định: D = ℝ
– Ta có: a = 1; b = –2; c = –3; = – 4.1.(–3) = 16
– Toạ độ đỉnh I = =
– Trục đối xứng = 1
– Giao điểm của parabol với trục Oy là A(0; –3)
– Giao điểm của parabol với trục Ox là B (–1; 0); (3; 0)
– Điểm đối xứng với điểm A qua trục đối xứng x = 1 là D (2; –3)
Vẽ parabol qua các điểm trên:
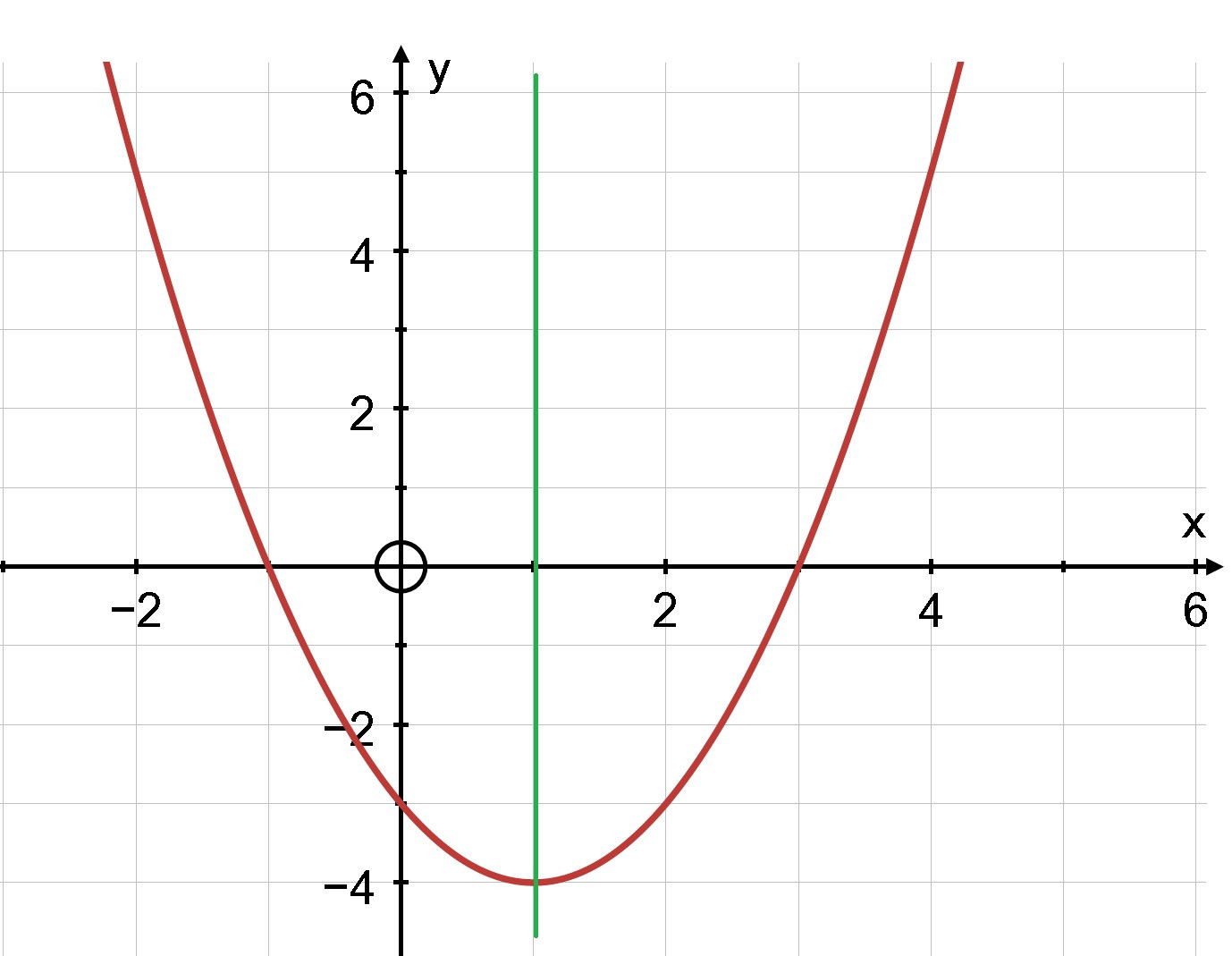
Chú ý:
Cho hàm số f(x) = (a ≠ 0)
– Nếu a > 0 thì hàm số nghịch biến trên khoảng ; đồng biến trên khoảng .
– Nếu a < 0 thì hàm số đồng biến trên khoảng ; nghịch biến trên khoảng .
Bảng biến thiên:
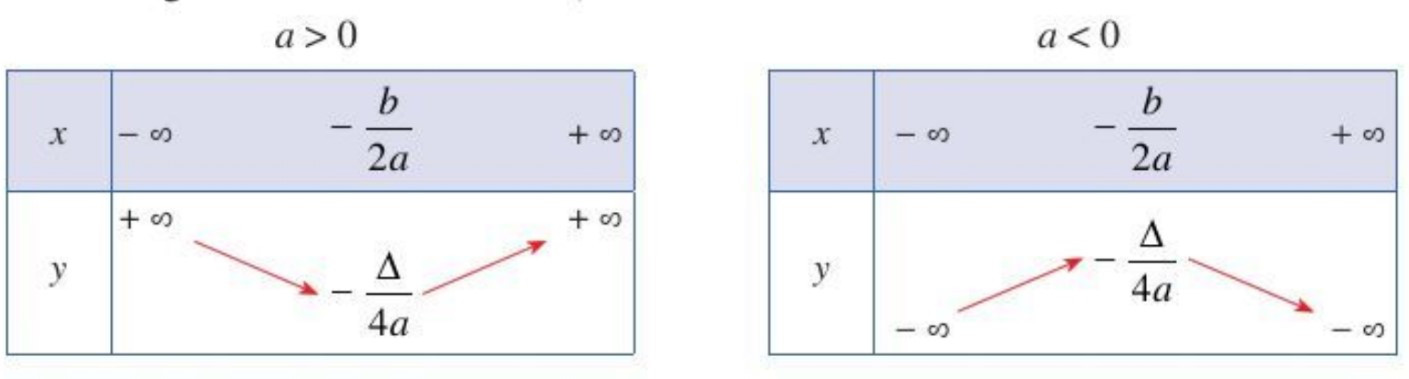
Bài giảng Toán 10 Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai - Cánh diều
Xem thêm các bài giải SGK Toán 10 Cánh diều hay, chi tiết khác:
Bài 3: Dấu của tam thức bậc hai
Bài 4: Bất phương trình bậc hai một ẩn
Bài 5: Hai dạng phương trình quy về phương trình bậc hai