Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài tập cuối chương 3 chi tiết sách Toán 7 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:
Giải bài tập Toán lớp 7 Bài tập cuối chương 3
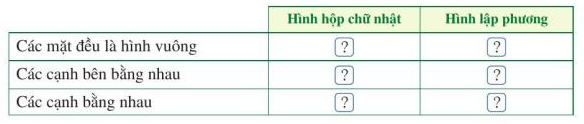
Phương pháp giải:
Đặc điểm của hình hộp chữ nhật, hình lập phương
Lời giải:
b) Cho một hình lăng trụ đứng có độ dài cạnh bên là 20 cm và đáy là một hình thang cân. Biết hình thang cân đó có độ dài cạnh bên là 13 cm, độ dài hai đáy lần lượt là 8 cm, 18 cm và chiều cao là 12 cm. Tính diện tích toàn phần ( tức là tổng diện tích các mặt) của hình lăng trụ đứng đã cho.
Phương pháp giải:
Diện tích xung quanh hình lăng trụ đứng: Sxq = Chu vi đáy. chiều cao
Diện tích toàn phần = diện tích xung quanh + diện tích 2 đáy
Lời giải:
a) Diện tích xung quanh hình lăng trụ đứng đó là:
Sxq = (4+5+6).10 = 150 (cm2 )
b) Chu vi đáy là: 8+18+13+13 = 52 (cm)
Diện tích đáy là: Sđáy = (8+18).12:2 = 156 (cm2)
Diện tích toàn phần của lăng trụ đó là:
Stp = Sxq + 2. Sđáy = 52. 20 +2. 156 = 1352 (cm2)
b) Một hình lập phương mới có độ dài cạnh gấp đôi độ dài cạnh của hình lập phương ban đầu. Tính thể tích của hình lập phương mới và cho biết thể tích của hình lập phương mới gấp bao nhiêu lần thể tích của hình lập phương ban đầu.
Phương pháp giải:
+) Thể tích của hình lập phương cạnh a là: V = a3
Lời giải:
a) Thể tích hình lập phương đó là:
V = 33 =27 (cm3)
b) Cạnh của hình lập phương mới là: 2. 3 = 6 (cm)
Thể tích của hình lập phương mới là: V’ = 63 = 216 (cm3)
Thể tích hình lập phương mới gấp số lần thể tích của hình lập phương ban đầu là:
216 : 27=8 (lần)
Chú ý: Khi tăng độ dài cạnh hình lập phương lên a lần thì thể tích hình lập phương tăng lên a3 lần.
Phương pháp giải:
Thể tích hình lăng trụ đứng: V= diện tích đáy. chiều cao
Lời giải:
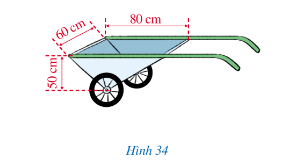
Thùng chứa là hình lăng trụ tam giác có cạnh bên là 60 cm, cạnh đáy là 80 cm, chiều cao ứng với đáy đó là 50 cm
Diện tích đáy của hình lăng trụ tam giác là: Sđáy = 50.80 : 2 = 2 000 (cm2)
Thùng chứa của xe chở hai bánh đó có thể tích bằng:
V = Sđáy . h = 2 000. 60 = 120 000 (cm3) = 120 lít
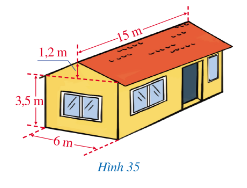
Phương pháp giải:
Phần không gian của ngôi nhà chia làm 2 phần: phần không gian có dạng hình hộp chữ nhật và hình lăng trụ đứng tam giác
Thể tích hình lăng trụ đứng: V1 = diện tích đáy. chiều cao
Thể tích hình hộp chữ nhật: V2 = chiều dài đáy . chiều rộng đáy. chiều cao
Lời giải:
Thể tích phần không gian có dạng hình lăng trụ tam giác là:
V1 = (6.1,2:2) . 15= 54 (m3)
Thể tích phần không gian có dạng hình hộp chữ nhật là:
V2 = 15.6.3,5 = 315 (m3)
Thể tích phần không gian được giới hạn bởi ngôi nhà đó là:
V = V1 + V2 = 54 + 315 = 369 (m3)
Lý thuyết Toán 7 Chương 3: Hình học trực quan
1. Hình hộp chữ nhật. Hình lập phương.
1.1 Hình hộp chữ nhật
- Hình hộp chữ nhật có 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo.
- Các mặt đều là hình chữ nhật.
- Các cạnh bên bằng nhau.
Chú ý: Để nhận dạng tốt hơn hình hộp chữ nhật, người ta vẽ các cạnh không nhìn thấy bằng nét đứt.
1.2. Hình lập phương
- Hình lập phương có 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo.
- Các mặt đều là hình vuông.
- Các cạnh đều bằng nhau.
1.3. Diện tích xung quanh và thể tích của hình hộp chữ nhật và hình lập phương
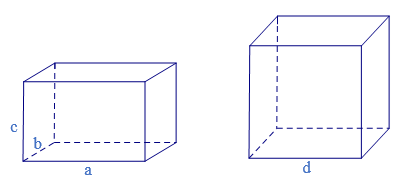
Cho hình hộp chữ nhật có ba kích thước: chiều dài a, chiều rộng là b, chiều cao là c (a, b, c cùng đơn vị đo). Cho hình lập phương có độ dài cạnh là d.
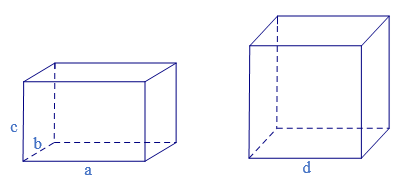
Ta có một số công thức sau:
|
|
Diện tích xung quanh |
Thể tích |
|
Hình hộp chữ nhật |
Sxq = 2(a + b)c |
V = abc |
|
Hình lập phương |
Sxq = 4d2 |
V = d3 |
2. Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác
2.1 Hình lăng trụ đứng tam giác
- Hình lăng trụ đứng tam giác có 5 mặt, 9 cạnh, 6 đỉnh.
- Hai mặt đáy cùng là tam giác và nằm trong hai mặt phẳng song song với nhau; Mỗi mặt bên là hình chữ nhật;
- Các cạnh bên bằng nhau;
- Chiều cao của hình lăng trụ đứng tam giác là độ dài cạnh bên.
2.2. Hình lăng trụ đứng tứ giác
- Lăng trụ đứng tứ giác có 6 mặt, 12 cạnh, 8 đỉnh.
- Hai mặt đáy cùng là tứ giác và song song với nhau. Mỗi mặt bên là hình chữ nhật.
- Các cạnh bên bằng nhau.
- Chiều cao của hình lăng trụ đứng tứ giác là độ dài một cạnh bên.
Chú ý: Hình hộp chữ nhật và hình lập phương cũng là lăng trụ đứng tứ giác.
2.3. Thể tích và diện tích xung quanh của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác
- Thể tích của hình lăng trụ đứng tứ giác bằng diện tích đáy nhân với chiều cao.
Tức là: V = S . h, trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tứ giác.
- Thể tích của hình lăng trụ đứng tam giác bằng diện tích đáy nhân với chiều cao.
Tức là: V = S . h, trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tam giác.
- Diện tích xung quanh của hình lăng trụ đứng tam giác hay hình lăng trụ đứng tứ giác bằng chu vi đáy nhân với chiều cao.
Tức là Sxq = C . h, trong đó Sxq là diện tích xung quanh, C là chu vi đáy, h là chiều cao của hình lăng trụ đứng tam giác hay của hình lăng trụ đứng tứ giác.
Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:
Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác
Hoạt động thực hành và trải nghiệm. Chủ đề 2: Tạo đồ dùng hình lăng trụ đứng
Bài 2: Tia phân giác của một góc
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
