Với giải sách bài tập Toán 7 Bài ôn tập chương 3 sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài ôn tập chương 3

Giải Toán 7 trang 94 Toán 7 Tập 1

Bài 16 trang 94 Toán 7 Tập 1: Trong các phát biểu sau, phát biểu nào đúng? A. Hình lăng trụ đứng tứ giác có 6 mặt, 8 đỉnh, 8 cạnh;

B. Hình lăng trụ đứng tứ giác có 4 mặt, 6 đỉnh, 8 cạnh;

C. Hình lăng trụ đứng tứ giác có 4 mặt, 8 đỉnh, 12 cạnh;

D. Hình lăng trụ đứng tứ giác có 6 mặt, 8 đỉnh, 12 cạnh.

Lời giải

Đáp án đúng là: D

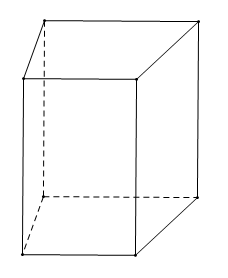
Hình lăng trụ đứng tứ giác có 6 mặt, 8 đỉnh, 12 cạnh.

Vậy ta chọn phương án D.

Bài 17 trang 94 Toán 7 Tập 1: Một hình lập phương có thể tích là 125 m³. Diện tích xung quanh của hình lập phương đó là:

A. 125 m²;

B. 500 m²;

C. 150 m²;

D. 100 m².

Lời giải

Đáp án đúng là: D

Thể tích của hình lập phương có độ dài cạnh là d (m) (d > 0) là: d³ (m³).

Mà theo bài thể tích của hình lập phương này bằng 125 m³

Do đó d³ = 125

Hay d³ = 5³

Suy ra d = 5 (m).

Diện tích xung quanh của hình lập phương đó là:

4.5² = 100 (m²).

Vậy ta chọn phương án D.

Bài 18 trang 94 Toán 7 Tập 1: Một bể rỗng không chứa nước có dạng hình hộp chữ nhật với chiều dài là 2,4 m, chiều rộng là 1,5 m, chiều cao là 1 m. Người ta sử dụng một máy bơm nước có công suất 30 l/phút để bơm đầy bể đó. Số giờ để bể đó đầy nước là:

A. $\frac{13}{3}$ giờ;

B. 120 giờ;

C. 2 giờ;

D. $\frac{49}{18}$ giờ.

Lời giải

Đáp án đúng là: C

Thể tích của bể chính là thể tích của hình hộp chữ nhật với chiều dài là 2,4 m, chiều rộng là 1,5 m, chiều cao là 1 m.

Do đó thể tích của bể đó là:

2,4.1,5.1 = 3,6 (m³) = 3 600 (l).

Người ta sử dụng một máy bơm nước có công suất 30 l/phút để bơm đây bể đó nên cứ một phút bể bơm được 30 lít nước.

Thời gian để bể đầy nước là:

3 600 : 30 = 120 (phút) = 2 (giờ).

Vậy sau 2 giờ thì bể đầy nước.

Ta chọn phương án C.

Bài 19 trang 94 Toán 7 Tập 1: Cho hình hộp chữ nhật ABCD.A’B’C’D’ với các kích thước AB = 20 cm, BC = 15 cm, CC’ = 12 cm (Hình 22).

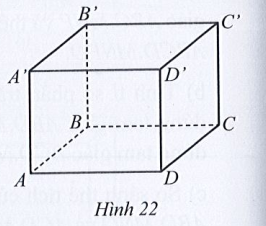
Tỉ số diện tích xung quanh và tổng diện tích hai đáy của hình hộp chữ nhật đó là:

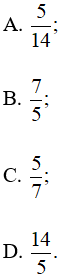
Lời giải

Đáp án đúng là: B

Diện tích xung quanh của hình hộp chữ nhật là:

2.(20 + 15).12 = 840 (cm²).

Diện tích hai mặt đáy của hình hộp chữ nhật là:

2.20.15 = 600 (cm²).

Tỉ số diện tích xung quanh và tổng diện tích hai đáy của hình hộp chữ nhật đó là:

$\frac{840}{600}=\frac{7}{5}.$

Vậy ta chọn phương án B.

Bài 20 trang 94 Toán 7 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) Diện tích xung quanh của hình hộp chữ nhật bằng một nửa tổng diện tích các mặt.

b) Thể tích của hình hộp chữ nhật bằng tích chiều dài nhân với chiều rộng rồi nhân với chiều cao.

c) Diện tích xung quanh của hình lập phương bằng diện tích của một mặt nhân với 6.

d) Thể tích của hình lập phương bằng tích của cạnh nhân cạnh rồi nhân với cạnh.

Lời giải

a) Diện tích xung quanh của hình hộp chữ nhật bằng một nửa tổng diện tích các mặt là phát biểu sai.

b) Thể tích của hình hộp chữ nhật bằng tích chiều dài nhân với chiều rộng rồi nhân với chiều cao là phát biểu đúng.

c) Diện tích xung quanh của hình lập phương bằng diện tích của một mặt nhân với 6 là phát biểu sai vì diện tích xung quanh của hình lập phương bằng diện tích của một mặt nhân với 4.

d) Thể tích của hình lập phương bằng tích của cạnh nhân cạnh rồi nhân với cạnh là phát biểu đúng.

Vậy trong các phát biểu trên, phát biểu đúng là b, d; phát biểu sau là a, c.

Bài 21 trang 94, 95 Toán 7 Tập 1:

a) Một hình lập phương có thể tích là 216 dm³. Tính diện tích xung quanh của hình lập phương đó.

b) Hình hộp chữ nhật thứ nhất có các kích thước: chiều dài, chiều rộng, chiều cao lần lượt bằng a (m), b (m), c (m). Hình hộp chữ nhật thứ hai có các kích thước: chiều dài, chiều rộng, chiều cao lần lượt bằng 3a (m), 2b (m), 4c (m). Tính tỉ số giữa thể tích của hình hộp chữ nhật thứ hai và thể tích của hình hộp chữ nhật thứ nhất.

Lời giải

a) Gọi d (dm) là độ dài cạnh của hình lập phương (d > 0).

Khi đó thể tích của hình lập phương là d³ (dm³).

Theo bài thể tích của hình lập phương là 216 dm³ nên ta có:

d³ = 216

Hay d³ = 6³

Suy ra d = 6.

Diện tích xung quanh của hình lập phương là:

4.6² = 144 (dm²).

Vậy diện tích xung quanh của hình lập phương là 144 dm².

b) Thể tích hình hộp chữ nhật thứ nhất là: abc (m³).

Thể tích hình hộp chữ nhật thứ hai là: 3a . 2b . 4c = 24abc (m³).

Tỉ số giữa thể tích của hình hộp chữ nhật thứ hai và thể tích của hình hộp chữ nhật thứ nhất là: (24abc) : (abc) = 24.

Vậy tỉ số giữa thể tích của hình hộp chữ nhật thứ hai và thể tích của hình hộp chữ nhật thứ nhất bằng 24.

Giải Toán 7 trang 95 Tập 1

Bài 22* trang 95 Toán 7 Tập 1: Một hình lăng trụ đứng tứ giác có chu vi đáy là 12 dm. Nếu tăng chiều cao thêm 2 dm và giảm chu vi đáy đi 4 dm thì diện tích xung quanh của hình lăng trụ đứng đã cho giảm 20 dm². Tính diện tích xung quanh của hình lăng trụ đứng ban đầu.

Lời giải

Gọi độ dài cạnh bên (chiều cao) của hình lăng trụ đứng tứ giác ban đầu là x (dm) (x > 0).

Khi đó, diện tích xung quanh của hình lăng trụ đứng ban đầu là 12x (dm²).

Nếu tăng chiều cao thêm 2 dm thì hình lăng trụ mới có chiều cao là x + 2 (dm).

Nếu giảm chu vi đáy đi 4 dm thì hình lăng trụ mới có chu vi đáy là: 12 – 4 = 8 (dm).

Diện tích xung quanh của hình lăng trụ đứng mới là:

8.(x + 2) = 8x + 16 (dm²).

Theo bài nếu tăng chiều cao thêm 2 dm và giảm chu vi đáy đi 4 dm thì diện tích xung quanh của hình lăng trụ đứng đã cho giảm 20 dm² nên ta có:

12x − 20 = 8x + 16

Suy ra 12x – 8x = 16 + 20

Hay 4x = 36

Do đó x = 9 (dm).

Vậy diện tích xung quanh của hình lăng trụ đứng ban đầu là: 12.9 = 108 (dm²).

Bài 23 trang 95 Toán 7 Tập 1:

a) Một hình lăng trụ đứng tam giác có độ dài cạnh bên bằng 16 cm và đáy là tam giác với độ dài các cạnh lần lượt là 4 cm, 8 cm, 11 cm. Tính diện tích xung quanh của hình lăng trụ đó.

b) Một hình lăng trụ đứng tứ giác có đáy là hình thoi với độ dài cạnh đáy bằng 17 cm. Tính chiều cao của hình lăng trụ đó, biết các đường chéo của đáy lần lượt bằng 16 cm, 30 cm và diện tích toàn phần của hình lăng trụ (tức là tổng diện tích các mặt) bằng 1 840 cm².

c) Một hình lăng trụ đứng tứ giác có độ dài cạnh bên là 12 cm và đáy là hình thang với độ dài đáy bé, đáy lớn, đường cao lần lượt là 15 cm, 17 cm, 13 cm. Tính thể tích của hình lăng trụ đó.

Lời giải

a) Diện tích xung quanh của hình lăng trụ đứng tam giác đó là:

(4 + 8 + 11). 16 = 368 (cm²).

b) Diện tích hai mặt đáy của hình lăng trụ đứng tứ giác đó là:

2.$\frac{16.30}{2}$ = 480 (cm²).

Diện tích xung quanh của hình lăng trụ đứng tứ giác đó là:

1 840 – 480 = 1 360 (cm²).

Chu vi mặt đáy hình thoi của hình lăng trụ đứng tứ giác đó là:

4.17 = 68 (cm).

Chiều cao của hình lăng trụ đứng tứ giác đó là:

1 360 : 68 = 20 (cm).

Vậy chiều cao của hình lăng trụ đứng tứ giác là 20 cm.

c) Diện tích đáy của hình lăng trụ đứng tứ giác đó là:

$\frac{1}{2}$.(15 + 17).13 = 208 (cm²).

Thể tích của hình lăng trụ tứ giác đó là:

208 . 12 = 2 496 (cm³).

Vậy thể tích của hình lăng trụ tứ giác đó là 2 496 cm³.

Bài 24* trang 95 Toán 7 Tập 1: Hình 23 minh hoạ các mặt của một hình được ghép bởi nhiều khối lập phương nhỏ cạnh 1 cm.

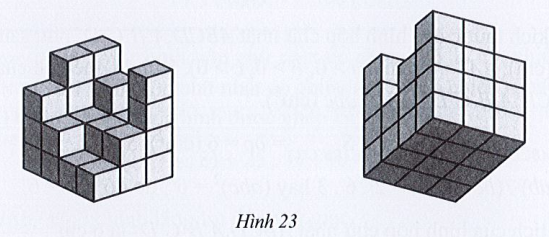
a) Hình được ghép có bao nhiêu khối lập phương nhỏ cạnh 1 cm?

b) Tính thể tích của hình được ghép.

c) Người ta sơn màu lên bề ngoài của hình được ghép. Có bao nhiêu khối lập phương nhỏ cạnh 1 cm không được sơn mặt nào?

Lời giải

a) Có 4 lớp tính từ dưới lên:

• Lớp dưới cùng (gọi là lớp thứ nhất) có: 4 . 3 = 12 khối lập phương nhỏ cạnh 1 cm;

• Lớp tiếp theo (gọi là lớp thứ hai) có: 12 – 2 = 10 khối lập phương nhỏ cạnh 1 cm;

• Lớp thứ ba có 5 khối lập phương nhỏ cạnh 1 cm;

• Lớp trên cùng có 3 khối lập phương nhỏ cạnh 1 cm.

Vậy hình được ghép có: 12 + 10 + 5 + 3 = 30 khối lập phương nhỏ cạnh 1 cm.

b) Thể tích của mỗi khối lập phương nhỏ cạnh 1 cm là 1 cm³.

Do đó thể tích của hình được ghép (gồm 30 khối lập phương nhỏ cạnh 1 cm) là:

30.1 = 30 (cm³).

Vậy thể tích của hình được ghép là 30 cm³.

c) Do sơn màu lên bề ngoài của hình được ghép nên khối lập phương nhỏ nào cũng có mặt được sơn.

Vậy số khối lập phương nhỏ cạnh 1 cm không được sơn mặt nào là: 0.

Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác

Bài ôn tập chương 3

Bài 1 : Góc ở vị trí đặc biệt

Bài 2 : Tia phân giác của một góc

Bài 3 : Hai đường thẳng song song

Lý thuyết Toán 7 Chương 3: Hình học trực quan

1. Hình hộp chữ nhật. Hình lập phương.
1.1 Hình hộp chữ nhật

- Hình hộp chữ nhật có 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo.

- Các mặt đều là hình chữ nhật.

- Các cạnh bên bằng nhau.

Chú ý: Để nhận dạng tốt hơn hình hộp chữ nhật, người ta vẽ các cạnh không nhìn thấy bằng nét đứt.

1.2. Hình lập phương

- Hình lập phương có 6 mặt, 12 cạnh, 8 đỉnh, 4 đường chéo.

- Các mặt đều là hình vuông.

- Các cạnh đều bằng nhau.

1.3. Diện tích xung quanh và thể tích của hình hộp chữ nhật và hình lập phương

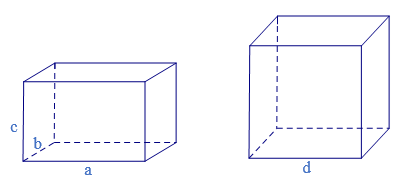
Cho hình hộp chữ nhật có ba kích thước: chiều dài a, chiều rộng là b, chiều cao là c (a, b, c cùng đơn vị đo). Cho hình lập phương có độ dài cạnh là d.

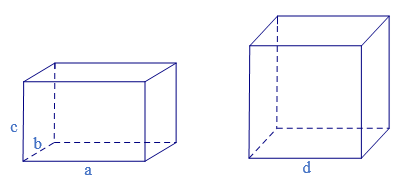
Ta có một số công thức sau:

2. Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác
2.1 Hình lăng trụ đứng tam giác

- Hình lăng trụ đứng tam giác có 5 mặt, 9 cạnh, 6 đỉnh.

- Hai mặt đáy cùng là tam giác và nằm trong hai mặt phẳng song song với nhau; Mỗi mặt bên là hình chữ nhật;

- Các cạnh bên bằng nhau;

- Chiều cao của hình lăng trụ đứng tam giác là độ dài cạnh bên.

2.2. Hình lăng trụ đứng tứ giác

- Lăng trụ đứng tứ giác có 6 mặt, 12 cạnh, 8 đỉnh.

- Hai mặt đáy cùng là tứ giác và song song với nhau. Mỗi mặt bên là hình chữ nhật.

- Các cạnh bên bằng nhau.

- Chiều cao của hình lăng trụ đứng tứ giác là độ dài một cạnh bên.

Chú ý: Hình hộp chữ nhật và hình lập phương cũng là lăng trụ đứng tứ giác.

2.3. Thể tích và diện tích xung quanh của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác

- Thể tích của hình lăng trụ đứng tứ giác bằng diện tích đáy nhân với chiều cao.

Tức là: V = S . h, trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tứ giác.

- Thể tích của hình lăng trụ đứng tam giác bằng diện tích đáy nhân với chiều cao.

Tức là: V = S . h, trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tam giác.

- Diện tích xung quanh của hình lăng trụ đứng tam giác hay hình lăng trụ đứng tứ giác bằng chu vi đáy nhân với chiều cao.

Tức là S_xq = C . h, trong đó S_xq là diện tích xung quanh, C là chu vi đáy, h là chiều cao của hình lăng trụ đứng tam giác hay của hình lăng trụ đứng tứ giác.