Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 7 Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác chi tiết sách Toán 7 Tập 1 Cánh diều giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7. Mời các bạn đón xem:
Giải bài tập Toán lớp 7 Bài 2: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác
Video bài giảng Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác - Cánh diều

Những hình khối có dạng như trên được gọi là hình gì?
Phương pháp giải:
Dựa vào hiểu biết thực tiễn
Lời giải:
Những hình khối như trên được gọi là hình lăng trụ.
I. Hình lăng trụ đứng tam giác
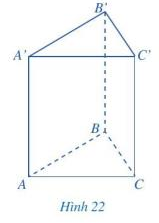
Phương pháp giải:
Đọc tên 5 mặt, 9 cạnh, 6 đỉnh của hình lăng trụ đứng tam giác
Lời giải:
Hình lăng trụ đứng tam giác có:
+) 5 mặt gồm: ABC; A’B’C’; ABB’A’; BCC’B’; ACC’A’
+) 9 cạnh gồm: AB; BC;CA;A’B’;B’C’;C’A’; AA’; BB’; CC’
+) 6 đỉnh gồm: A;B;C; A’;B’;C’.
a) Đáy dưới ABC và đáy trên A’B’C’ là hình gì?
b) Mặt bên AA’C’C là hình gì?
c) So sánh độ dài các cạnh bên AA’ và CC’
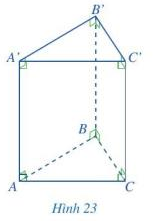
Phương pháp giải:
Hình lăng trụ đứng tam giác có 2 mặt đáy là hình tam giác, mặt bên là các hình chữ nhật
So sánh độ dài 2 cạnh
Lời giải:
a) Đáy dưới ABC và đáy trên A’B’C’ là hình tam giác
b) Mặt bên AA’C’C là hình chữ nhật
c) Hai cạnh bên AA’ và CC’ có độ dài bằng nhau
II. Hình lăng trụ đứng tứ giác
Phương pháp giải:
Đọc tên 6 mặt, 12 cạnh, 8 đỉnh của hình lăng trụ đứng tứ giác
Lời giải:
Hình lăng trụ đứng tứ giác ABCD. A’B’C’D’ có:
+) 6 mặt gồm: ABCD; A’B’C’D’; ABB’A’; ADD’A’; BCC’B’; CDD’C’.
+) 12 cạnh gồm: AB; BC;CD;DA;A’B’;B’C’;C’D’; D’A’; AA’; BB’; CC’ ; DD’.
+) 8 đỉnh gồm: A;B;C;D;A’;B’;C’;D’.
Hoạt động 6 trang 83 Toán lớp 7: Quan sát hình lập phương ABCD. A’B’C’D’ ở Hình 27 và cho biết:
a) Đáy dưới ABCD và đáy trên A’B’C’D’ là hình gì?
b) Mặt bên AA’D’D là hình gì?
c) So sánh độ dài hai cạnh bên AA’ và DD’.
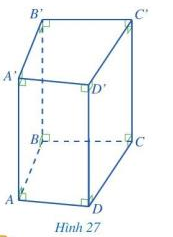
Phương pháp giải:
Hình lăng trụ đứng tứ giác có 2 mặt đáy là hình tứ giác, mặt bên là hình chữ nhật
Các cạnh bên bằng nhau
Lời giải:
a) Đáy dưới ABCD và đáy trên A’B’C’D’ là hình tứ giác
b) Mặt bên AA’D’D là hình chữ nhật
c) Độ dài hai cạnh bên AA’ và DD’ bằng nhau.
III. Thể tích và diện tích xung quanh của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác
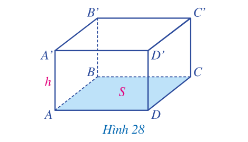
Tính thể tích hình hộp chữ nhật ABCD.A'B'C'D' theo S và h.
Phương pháp giải:
Công thức tính thể tích hình hộp chữ nhật
Lời giải:
Công thức tính thể tích hình hộp chữ nhật ABCD.A'B'C'D' là: V = S.h.
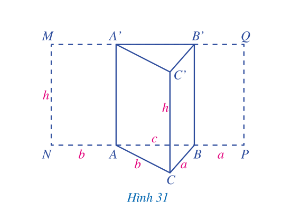
a) Tính diện tích hình chữ nhật MNPQ
b) So sánh diện tích của hình chữ nhật MNPQ với tích chu vi đáy của hình lăng trụ đứng tam giác ABC.A’B’C’ và chiều cao của hình lăng trụ đó.
c) So sánh diện tích của hình chữ nhật MNPQ với diện tích xung quanh của hình lăng trụ đứng tam giác ABC.A’B’C’
Phương pháp giải:
Diện tích hình chữ nhật = chiều dài . chiều rộng
Tính và so sánh
Lời giải:
a) Diện tích hình chữ nhật MNPQ là: S = MN . NP = h.(b+c+a)
b) Chu vi đáy của hình lăng trụ tam giác là: CABC = a+b+c
Tích chu vi đáy của hình lăng trụ đứng tam giác ABC.A’B’C’ và chiều cao của hình lăng trụ đó là:
(a+b+c).h
Như vậy, diện tích của hình chữ nhật MNPQ bằng tích chu vi đáy của hình lăng trụ đứng tam giác ABC.A’B’C’ và chiều cao của hình lăng trụ đó
c) Diện tích xung quanh của hình lăng trụ đứng tam giác ABC.A’B’C’ là: Sxq = SABB’A’ + SACC’A’ + SBCC’B’ = h.c+h.b+h.a = h.(c+b+a)
Vậy diện tích của hình chữ nhật MNPQ bằng diện tích xung quanh của hình lăng trụ đứng tam giác ABC.A’B’C’
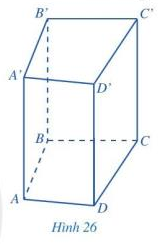
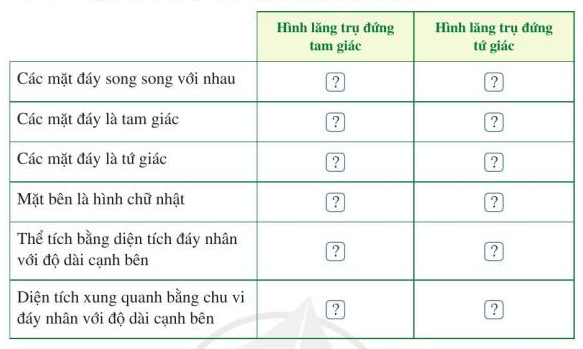
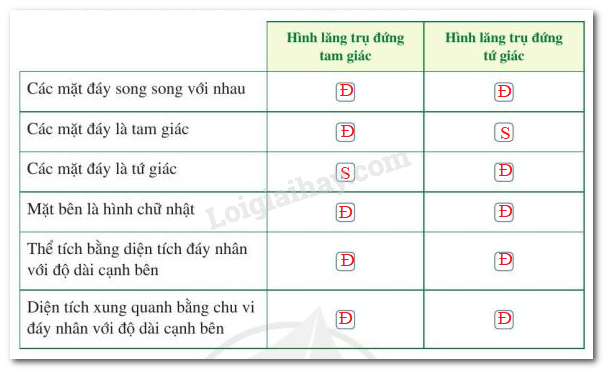
Bài 1 trang 85 Toán lớp 7: Quan sát Hình 22, Hình 26 và tìm số thích hợp cho ? trong bảng sau:
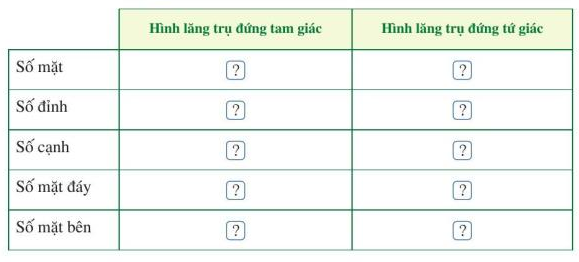
Phương pháp giải:
Đặc điểm của hình lăng trụ đứng tam giác và lăng trụ đứng tứ giác
Lời giải:
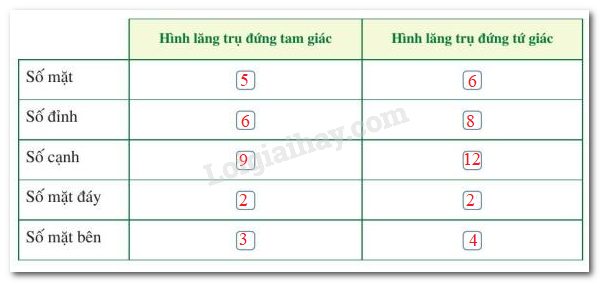
Phương pháp giải:
Đặc điểm của hình lăng trụ đứng tam giác và lăng trụ đứng tứ giác
Diện tích xung quanh, thể tích của hình lăng trụ đứng tam giác và lăng trụ đứng tứ giác
Lời giải:
Bài 3 trang 86 Toán lớp 7: Cho các hình lăng trụ đứng Hình 33a và Hình 33b:
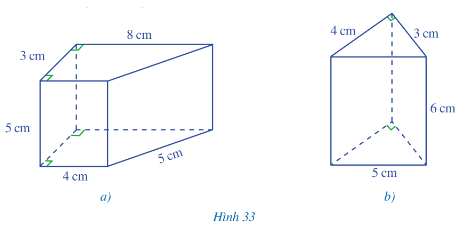
(i) Hình nào trong các hình 33a, 33b là hình lăng trụ đứng tam giác? Hình lăng trụ đứng tứ giác?
(ii) Tính diện tích xung quanh của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác ở Hình 33.
(iii) Tính thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác có ở Hình 33.
Phương pháp giải:
+) Hình lăng trụ đứng tam giác có 2 mặt đáy cùng là hình tam giác và song song với nhau; mỗi mặt bên là hình chữ nhật.
+) Hình lăng trụ đứng tứ giác có 2 mặt đáy cùng là hình tứ giác và song song với nhau; mỗi mặt bên là hình chữ nhật.
+) Diện tích xung quanh của hình lăng trụ đứng = chu vi đáy . chiều cao
+) Thể tích của hình lăng trụ đứng = diện tích đáy . chiều cao
Lời giải:
(i) Trong hình 33a, 33b ta thấy hình 33b là hình lăng trụ đứng tam giác, hình 33a là hình lăng trụ đứng tứ giác.
(ii)
+) Hình lăng trụ đứng tam giác (Hình 33b)
Chu vi đáy là: 3 + 4 + 5 = 12 (cm)
Diện tích xung quanh là: Sxq = 12.6 = 72 (cm2)
+) Hình lăng trụ đứng tứ giác (Hình 33a)
Chu vi đáy là: 3 + 4 + 5 + 8 = 20 (cm)
Diện tích xung quanh là: Sxq = 20.5 = 100 (cm2).
(iii)
+) Hình lăng trụ đứng tam giác (Hình 33b)
Diện tích đáy là: S = (cm2)
Thể tích hình lăng trụ đứng tam giác là: V = S.h = 6.6 = 36 (cm3)
+) Hình lăng trụ đứng tứ giác (hình 33a)
Diện tích đáy là: S = = 30 (cm2)
Thể tích hình lăng trụ đứng tứ giác là: V = S.h = 30.5 = 150 (cm3).
Lý thuyết Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác
1. Hình lăng trụ đứng tam giác
- Hình lăng trụ đứng tam giác có 5 mặt, 9 cạnh, 6 đỉnh.
- Hai mặt đáy cùng là tam giác và nằm trong hai mặt phẳng song song với nhau; Mỗi mặt bên là hình chữ nhật;
- Các cạnh bên bằng nhau;
- Chiều cao của hình lăng trụ đứng tam giác là độ dài cạnh bên.
Ví dụ:
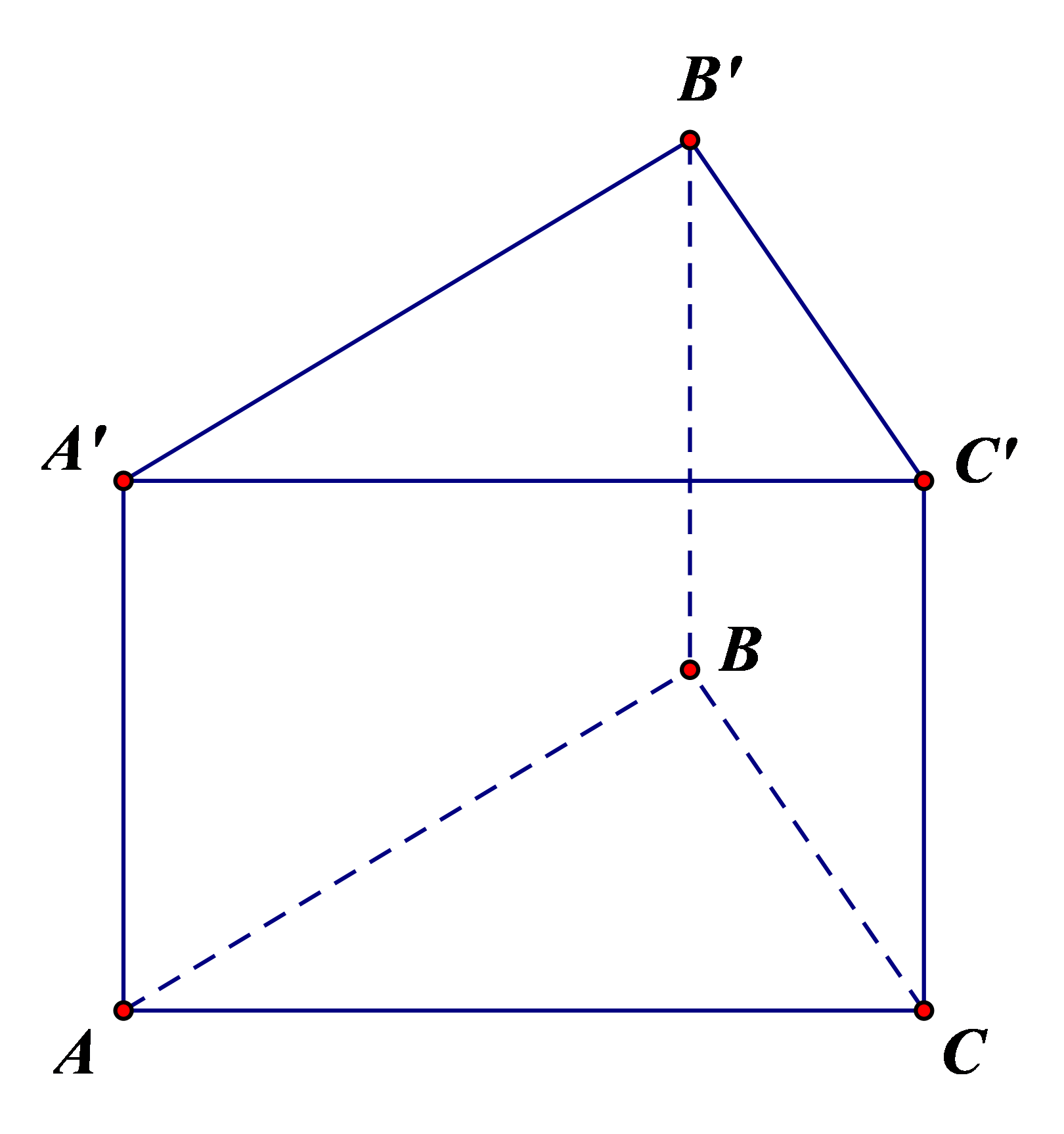
Hình lăng trụ đứng tam giác ABC.A'B'C' có:
- Đáy dưới là tam giác ABC, đáy trên là tam giác A'B'C';
Các mặt bên là các hình chữ nhật: AA'B'B, BB'C'C, CC'A'A;
- Các cạnh:
+ Cạnh đáy: AB, BC, CA, A'B', B'C', C'A'
+ Cạnh bên: AA', BB', CC';
- Các đỉnh: A, B, C, A', B', C'.
- Chiều cao là độ dài một cạnh bên: AA' hoặc BB' hoặc CC'.
2. Hình lăng trụ đứng tứ giác
- Lăng trụ đứng tứ giác có 6 mặt, 12 cạnh, 8 đỉnh.
- Hai mặt đáy cùng là tứ giác và song song với nhau. Mỗi mặt bên là hình chữ nhật.
- Các cạnh bên bằng nhau.
- Chiều cao của hình lăng trụ đứng tứ giác là độ dài một cạnh bên.
Ví dụ:
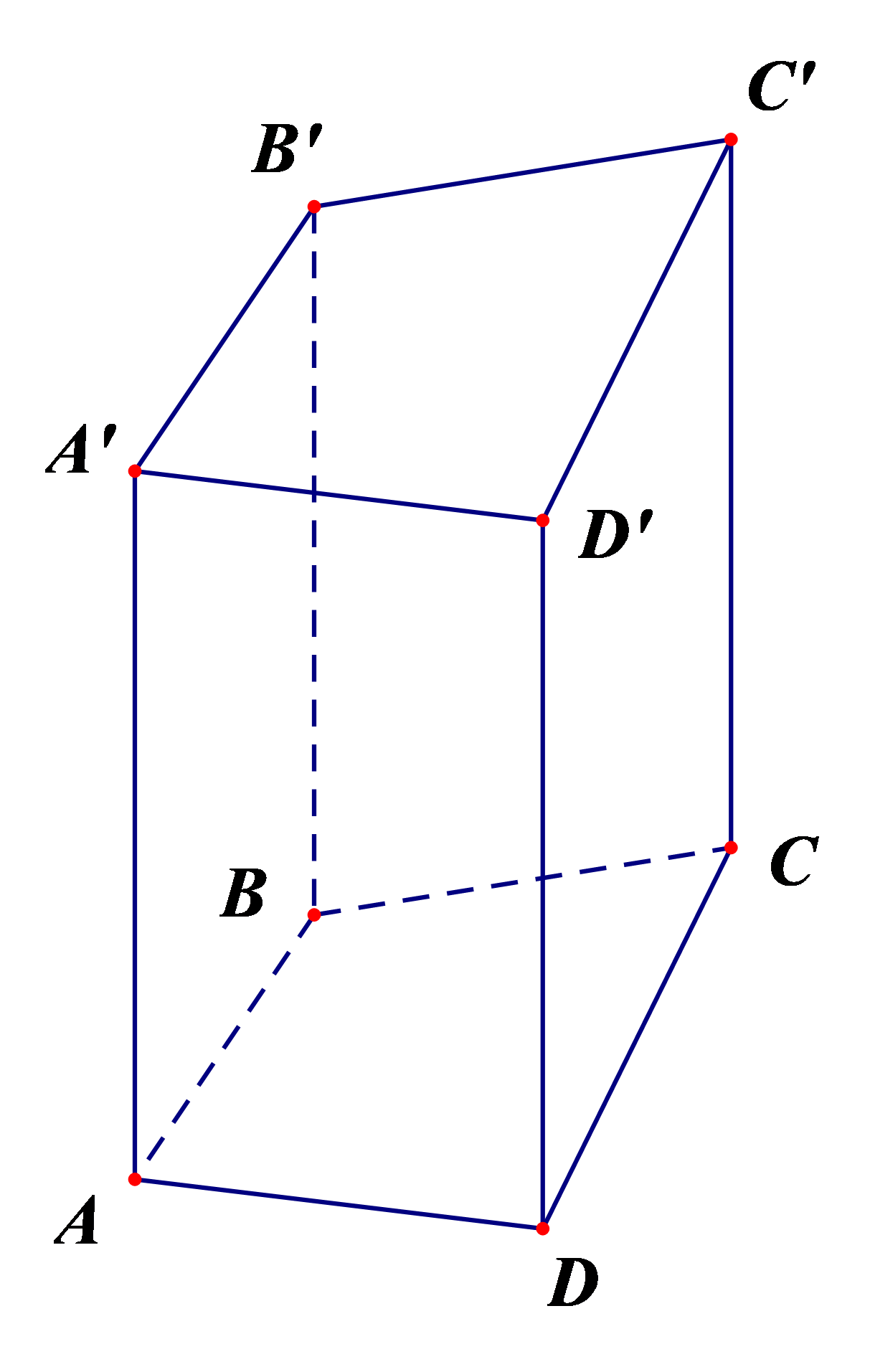
Hình lăng trụ đứng tứ giác ABCD.A'B'C'D' có:
- Đáy dưới là tứ giác ABCD, đáy trên là tứ giác A'B'C'D';
Các mặt bên là các hình chữ nhật: AA'B'B, BB'C'C, CC'D'D, DD'A'A;
- Các cạnh:
+ Cạnh đáy: AB, BC, CD, DA, A'B', B'C', C'D', D'A'
+ Các cạnh bên: AA', BB', CC', DD' bằng nhau.
- Các đỉnh: A, B, C, D, A', B', C', D'.
- Chiều cao là độ dài một cạnh bên: AA' hoặc BB' hoặc CC' hoặc DD'.
Chú ý: Hình hộp chữ nhật và hình lập phương cũng là lăng trụ đứng tứ giác.
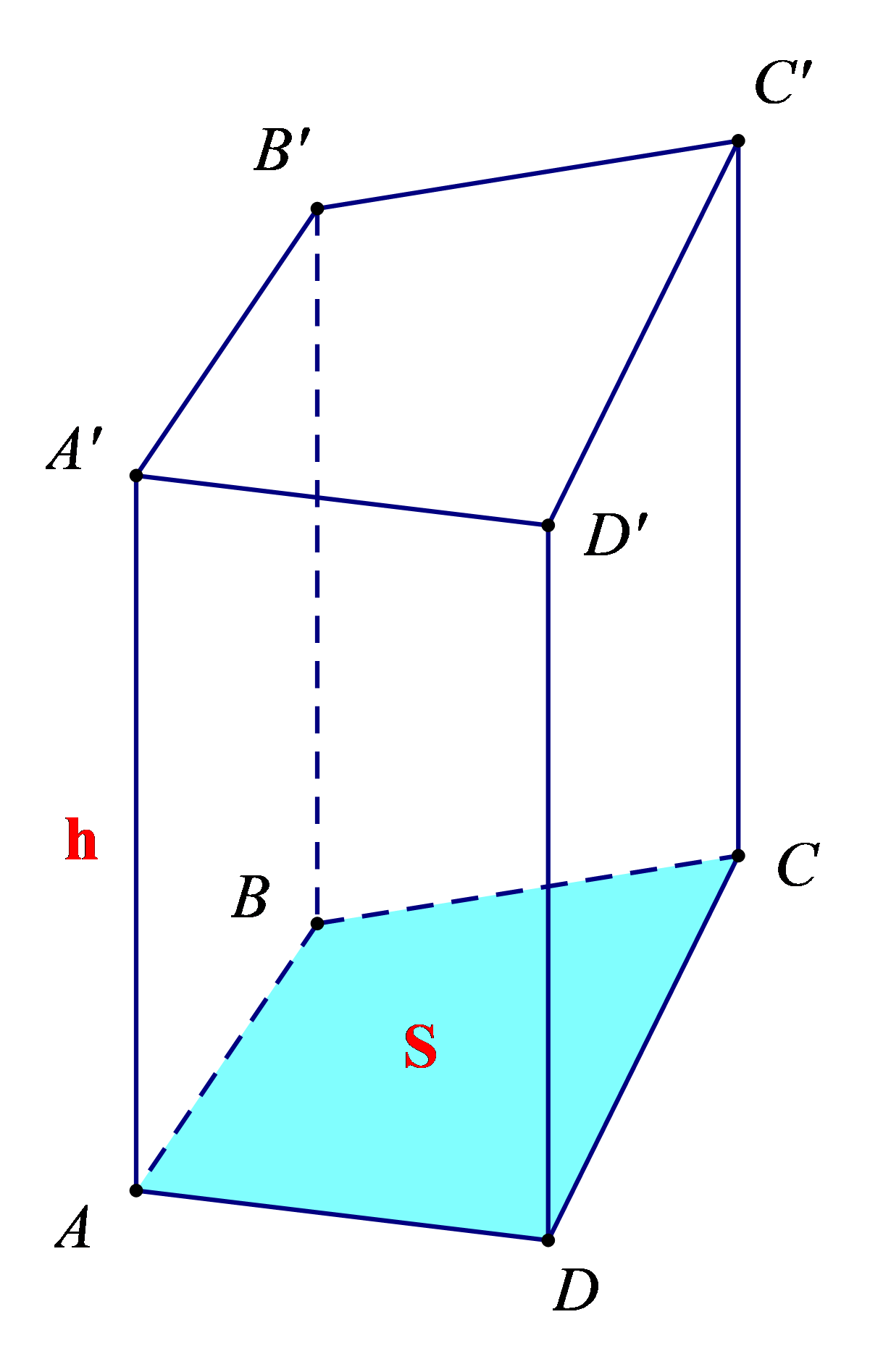
3. Thể tích và diện tích xung quanh của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác
- Thể tích của hình lăng trụ đứng tứ giác bằng diện tích đáy nhân với chiều cao.
Tức là: V = S . h, trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tứ giác.
- Thể tích của hình lăng trụ đứng tam giác bằng diện tích đáy nhân với chiều cao.
Tức là: V = S . h, trong đó V là thể tích, S là diện tích đáy và h là chiều cao của hình lăng trụ đứng tam giác.
- Diện tích xung quanh của hình lăng trụ đứng tam giác hay hình lăng trụ đứng tứ giác bằng chu vi đáy nhân với chiều cao.
Tức là Sxq = C . h, trong đó Sxq là diện tích xung quanh, C là chu vi đáy, h là chiều cao của hình lăng trụ đứng tam giác hay của hình lăng trụ đứng tứ giác.
Ví dụ:

a) Cho hình lăng trụ đứng tam giác ABC.A'B'C'.
Sxq = C . h, trong đó C là chu vi của tam giác ABC (hoặc tam giác A'B'C'), h là độ dài cạnh bên AA' (hoặc BB, hoặc CC').
V = S . h, trong đó S là diện tích tam giác ABC (hoặc A'B'C'), h là độ dài cạnh bên AA' (hoặc BB' hoặc CC').
b) Cho hình lăng trụ đứng tứ giác ABCD.A'B'C'D':
Sxq = C . h, trong đó C là chu vi của tứ giác ABCD (hoặc tứ giác A'B'C'D'), h là độ dài cạnh bên AA' (hoặc BB, hoặc CC', hoặc DD').
V = S . h, trong đó S là diện tích tứ giác ABCD (hoặc A'B'C'D'), h là độ dài cạnh bên AA' (hoặc BB' hoặc CC', hoặc DD').
Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:
Bài 1: Hình hộp chữ nhật. Hình lập phương
Hoạt động thực hành và trải nghiệm. Chủ đề 2: Tạo đồ dùng hình lăng trụ đứng
Bài 1: Góc ở vị trí đặc biệt