Giải Toán 8 Bài 9: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp

hoa Ngày: 26-09-2022 Lớp 8

3 K

Tailieumoi.vn giới thiệu Giải bài tập Toán 8 Bài 9: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp, chi tiết nhất giúp học sinh dễ dàng làm bài tập Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp lớp 8.

Giải bài tập Toán lớp 8 Bài 9: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp

Trả lời câu hỏi giữa bài

Trả lời câu hỏi 1 trang 23 sgk Toán 8 Tập 1: Phân tích đa thức $2 x^{3} y - 2 x y^{3} - 4 x y^{2} - 2 x y$ thành nhân tử.

Phương pháp giải: Áp dụng phương pháp phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung và phương pháp dùng hằng đẳng thức.

$1) {(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

$3) A^{2} - B^{2} = (A + B) (A - B)$

Lời giải:

$\begin{aligned} 2 x^{3} y - 2 x y^{3} - 4 x y^{2} - 2 x y \\ = 2 x y (x^{2} - y^{2} - 2 y - 1) \\ = 2 x y [x^{2} - (y^{2} + 2 y + 1)] \\ = 2 x y [x^{2} - {(y + 1)}^{2}] \\ = 2 x y [x + (y + 1)] . [x - (y + 1)] \\ = 2 x y (x + y + 1) (x - y - 1) \end{aligned}$

Trả lời câu hỏi 2 trang 23 sgk Toán 8 Tập 1:

a) Tính nhanh giá trị của biểu thức $x^{2} + 2 x + 1 - y^{2}$ tại x = 94,5 và y = 4,5

Phương pháp giải: Áp dụng: Phương pháp phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung, dùng hằng đẳng thức, phương pháp nhóm hạng tử.

$1) {(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

$3) A^{2} - B^{2} = (A + B) (A - B)$

Lời giải:

$x^{2} + 2 x + 1 - y^{2}$

$= (x^{2} + 2 x + 1) - y^{2}$

$= (x + 1)^{2} - y^{2}$

$= (x + 1 + y) (x + 1 - y)$

$= (x + y + 1) (x - y + 1)$

Thay $x = 94, 5$ và $y = 4, 5$ ta có:

$(x + y + 1) (x - y + 1)$

$= (94, 5 + 4, 5 + 1) (94, 5 - 4, 5 + 1)$

$= 100.91$

$= 9100$

b) Khi phân tích đa thức $x^{2} + 4 x - 2 x y - 4 y + y^{2}$ thành nhân tử, bạn Việt làm như sau:

$\begin{aligned} x^{2} + 4 x - 2 x y - 4 y + y^{2} \\ = (x^{2} - 2 x y + y^{2}) + (4 x - 4 y) \\ = {(x - y)}^{2} + 4 (x - y) \\ = (x - y) (x - y + 4) \end{aligned}$

Em hãy chỉ rõ trong cách làm trên, bạn Việt đã sử dụng những phương pháp nào để phân tích đa thức thành nhân tử.

Lời giải:

$x^{2} + 4 x - 2 x y - 4 y + y^{2}$ $= (x^{2} - 2 x y + y^{2}) + (4 x - 4 y)$ ( Bạn Việt dùng phương pháp nhóm hạng tử)

$= (x - y)^{2} + 4 (x - y)$ (Bạn Việt dùng phương pháp dùng hằng đẳng thức và đặt nhân tử chung)

$= (x - y) (x - y + 4)$ (Bạn Việt dùng phương pháp đặt nhân tử chung).

Câu hỏi và bài tập (trang 24, 25 sgk Toán 8 Tập 1)

Bài 51 trang 24 sgk Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) $x^{3} - 2 x^{2} + x$ ;

Phương pháp giải: - Áp dụng các phương pháp phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung, nhóm hạng tử, dùng hằng đẳng thức.

- Áp dụng hằng đẳng thức: $\begin{aligned} {(A - B)}^{2} = A^{2} - 2 A B + B^{2} \end{aligned}$

Lời giải:

$x^{3} - 2 x^{2} + x$

$= x . x^{2} - x .2 x + x$

$= x (x^{2} - 2 x + 1)$

$= x (x^{2} - 2 x .1 + 1^{2})$

$= x {(x - 1)}^{2}$

b) $2 x^{2} + 4 x + 2 - 2 y^{2}$ ;

Phương pháp giải: - Áp dụng các phương pháp phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung, nhóm hạng tử, dùng hằng đẳng thức.

- Áp dụng các hằng đẳng thức: $\begin{aligned} {(A + B)}^{2} = A^{2} + 2 A B + B^{2} \\ A^{2} - B^{2} = (A - B) (A + B) \end{aligned}$

Lời giải:

$2 x^{2} + 4 x + 2 - 2 y^{2}$

$= 2 (x^{2} + 2 x + 1 - y^{2})$

$= 2 [(x^{2} + 2 x + 1) - y^{2}]$

$= 2 [{(x + 1)}^{2} - y^{2}]$

$= 2 (x + 1 - y) (x + 1 + y)$

c) $2 x y - x^{2} - y^{2} + 16$ .

Phương pháp giải: - Áp dụng các phương pháp phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung, nhóm hạng tử, dùng hằng đẳng thức.

- Áp dụng các hằng đẳng thức: $\begin{aligned} {(A - B)}^{2} = A^{2} - 2 A B + B^{2} \\ A^{2} - B^{2} = (A - B) (A + B) \end{aligned}$

Lời giải:

$2 x y - x^{2} - y^{2} + 16$

$= 16 - (x^{2} - 2 x y + y^{2})$

$= 4^{2} - {(x - y)}^{2}$

$= [4 - (x - y)] . [4 + (x - y)]$

$= (4 - x + y) (4 + x - y)$

Bài 52 trang 24 sgk Toán 8 Tập 1: Chứng minh rằng $(5 n + 2)^{2} - 4$ chia hết cho $5$ với mọi số nguyên $n$ .

Phương pháp giải: Áp dụng tính chất chia hết của một tích: Nếu trong một tích các số nguyên có một thừa số chia hết cho một số nào đó thì tích cũng chia hết cho số đó.

Sử dụng: $A^{2} - B^{2} = (A + B) (A - B)$

Lời giải:

Ta có :

$(5 n + 2)^{2} - 4$

$= (5 n + 2)^{2} - 2^{2}$

$= (5 n + 2 - 2) (5 n + 2 + 2)$

$= 5 n (5 n + 4)$

Mà $5$ $⋮$ $5$ nên tích $5 n (5 n + 4)$ $⋮$ $5$ với $n \in Z$

Vậy $5 n (5 n + 4)$ $⋮$ $5$ với $n \in Z$ .

Bài 53 trang 24 sgk Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) $x^{2} - 3 x + 2$ ;

(Gợi ý: Ta không áp dụng ngay các phương pháp đã học để phân tích nhưng nếu tách hạng tử $- 3 x = - x - 2 x$ thì ta có $x^{2} - 3 x + 2 = x^{2} - x - 2 x + 2$ và từ đó dễ dàng phân tích tiếp.

Cũng có thể tách $2 = - 4 + 6$ , khi đó ta có $x^{2} - 3 x + 2 = x^{2} - 4 - 3 x + 6$ , từ đó dễ dàng phân tích tiếp)

Phương pháp giải: Áp dụng phương pháp: tách, nhóm, đặt nhân tử chung.

Cách 1: Tách $- 3 x = - x - 2 x$

Cách 2: Tách $2 = - 4 + 6$

Lời giải:

$x^{2} - 3 x + 2 = x^{2} - x - 2 x + 2$

$= (x^{2} - x) + (- 2 x + 2)$

$= (x . x - x) - (2 x - 2)$

$= x (x - 1) - 2 (x - 1)$

$= (x - 1) (x - 2)$

Cách 2:

$x^{2} - 3 x + 2 = x^{2} - 3 x - 4 + 6$

$= (x^{2} - 4) + (- 3 x + 6)$

$= (x^{2} - 2^{2}) - (3 x - 6)$

$= (x - 2) (x + 2) - 3 (x - 2)$

$= (x - 2) (x + 2 - 3)$

$= (x - 2) (x - 1)$

b) $x^{2} + x - 6$ ;

Phương pháp giải: Áp dụng phương pháp: tách, nhóm, đặt nhân tử chung.

Cách 1: Tách $x = 3 x - 2 x$

Cách 2:

Thêm bớt để xuất hiện hằng đẳng thức ${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$ và

$A^{2} - B^{2} = (A + B) (A - B)$

Lời giải:

$x^{2} + x - 6$

Tách $x = 3 x - 2 x$ ta được:

$x^{2} + x - 6 = x^{2} + 3 x - 2 x - 6$

$= (x^{2} + 3 x) + (- 2 x - 6)$

$= (x^{2} + 3 x) - (2 x + 6)$

$= x (x + 3) - 2 (x + 3)$

$= (x + 3) (x - 2)$ .

Cách 2:

$\begin{array}{l} x^{2} + x - 6 \\ = x^{2} + 2. x . \frac{1}{2} + {(\frac{1}{2})}^{2} - {(\frac{1}{2})}^{2} - 6 \\ = {(x + \frac{1}{2})}^{2} - \frac{1}{4} - 6 \\ = {(x + \frac{1}{2})}^{2} - \frac{25}{4} \\ = {(x + \frac{1}{2})}^{2} - {(\frac{5}{2})}^{2} \\ = (x + \frac{1}{2} + \frac{5}{2}) (x + \frac{1}{2} - \frac{5}{2}) \\ = (x + 3) (x - 2) \end{array}$

c) $x^{2} + 5 x + 6$ .

Phương pháp giải: Áp dụng phương pháp: tách, nhóm, đặt nhân tử chung.

Cách 1: Tách $5 x = 2 x + 3 x$

Cách 2: Thêm bớt để xuất hiện hằng đẳng thức ${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$ và

$A^{2} - B^{2} = (A + B) (A - B)$

Lời giải:

$x^{2} + 5 x + 6$

Tách $5 x = 2 x + 3 x$ ta được:

$x^{2} + 5 x + 6 = x^{2} + 2 x + 3 x + 6$

$= (x^{2} + 2 x) + (3 x + 6)$

$= x (x + 2) + 3 (x + 2)$

$= (x + 2) (x + 3)$

Cách 2:

$\begin{array}{l} x^{2} + 5 x + 6 \\ = x^{2} + 2. x . \frac{5}{2} + {(\frac{5}{2})}^{2} - {(\frac{5}{2})}^{2} + 6 \\ = {(x + \frac{5}{2})}^{2} - \frac{25}{4} + 6 \\ = {(x + \frac{5}{2})}^{2} - \frac{1}{4} \\ = {(x + \frac{5}{2})}^{2} - {(\frac{1}{2})}^{2} \\ = (x + \frac{5}{2} + \frac{1}{2}) (x + \frac{5}{2} - \frac{1}{2}) \\ = (x + 3) (x + 2) \end{array}$

Bài 54 trang 24 sgk Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) $x^{3} + 2 x^{2} y + x y^{2} - 9 x$ ;

Phương pháp giải: - Áp dụng phân tích đa thức thành nhân tử bằng phương pháp nhóm, hằng đẳng thức, đặt nhân tử chung.

- Áp dụng hằng đẳng thức: $\begin{aligned} {(A + B)}^{2} = A^{2} + 2 A B + B^{2} \\ A^{2} - B^{2} = (A - B) (A + B) \end{aligned}$

Lời giải:

$x^{3} + 2 x^{2} y + x y^{2} - 9 x$

$= x (x^{2} + 2 x y + y^{2} - 9)$

$= x [(x^{2} + 2 x y + y^{2}) - 9]$

$= x [{(x + y)}^{2} - 3^{2}]$

$= x (x + y - 3) (x + y + 3)$

b) $2 x - 2 y - x^{2} + 2 x y - y^{2}$ ;

Phương pháp giải: - Áp dụng phân tích đa thức thành nhân tử bằng phương pháp nhóm, hằng đẳng thức, đặt nhân tử chung.

- Áp dụng hằng đẳng thức: $\begin{aligned} {(A - B)}^{2} = A^{2} - 2 A B + B^{2} \\ A^{2} - B^{2} = (A - B) (A + B) \end{aligned}$

Lời giải:

$2 x - 2 y - x^{2} + 2 x y - y^{2}$

$= (2 x - 2 y) - (x^{2} - 2 x y + y^{2})$

$= 2 (x - y) - {(x - y)}^{2}$

$= (x - y) [2 - (x - y)]$

$= (x - y) (2 - x + y)$

c) $x^{4} - 2 x^{2}$ .

Phương pháp giải: - Áp dụng phân tích đa thức thành nhân tử bằng phương pháp nhóm, hằng đẳng thức, đặt nhân tử chung.

- Áp dụng hằng đẳng thức: $\begin{aligned} A^{2} - B^{2} = (A - B) (A + B) \end{aligned}$

Lời giải:

$x^{4} - 2 x^{2} = x^{2} (x^{2} - 2)$

$= x^{2} (x^{2} - {(\sqrt{2})}^{2})$

$= x^{2} (x - \sqrt{2}) (x + \sqrt{2})$ .

Bài 55 trang 24 sgk Toán 8 Tập 1: Tìm $x$ , biết:

a) $x^{3} - \frac{1}{4} x = 0$ ;

b) $(2 x - 1)^{2} - (x + 3)^{2} = 0$ ;

c) $x^{2} (x - 3) + 12 - 4 x = 0$ .

Phương pháp giải: - Phân tích vế trái thành nhân tử rồi áp dụng tính chất:

$A . B . C = 0 \Rightarrow [\begin{array}{l} A = 0 \\ B = 0 \\ C = 0 \end{array}$

Lời giải:

Ta có:

$\begin{aligned} x^{3} - \frac{1}{4} x = 0 \\ x (x^{2} - \frac{1}{4}) = 0 \\ x [x^{2} - {(\frac{1}{2})}^{2}] = 0 \\ x (x - \frac{1}{2}) (x + \frac{1}{2}) = 0 \end{aligned}$

$\Rightarrow [\begin{array}{l} x = 0 \\ x - \frac{1}{2} = 0 \\ x + \frac{1}{2} = 0 \end{array} \Rightarrow [\begin{array}{l} x = 0 \\ x = \frac{1}{2} \\ x = - \frac{1}{2} \end{array}$

Vậy $x = 0, x = \frac{1}{2}, x = - \frac{1}{2}$

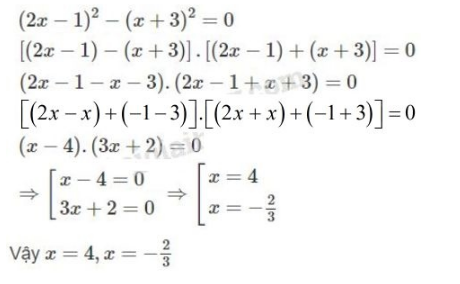
Giải Toán 8 Bài 9: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp (ảnh 1)

Ta có:

$\begin{aligned} x^{2} (x - 3) + 12 - 4 x = 0 \\ x^{2} (x - 3) + (- 4 x + 12) = 0 \\ x^{2} (x - 3) - (4 x - 12) = 0 \\ x^{2} (x - 3) - 4 (x - 3) = 0 \\ (x - 3) (x^{2} - 4) = 0 \\ (x - 3) (x - 2) (x + 2) = 0 \\ \Rightarrow [\begin{matrix} x - 3 = 0 \\ x - 2 = 0 \\ x + 2 = 0 \end{matrix} \Rightarrow [\begin{matrix} x = 3 \\ x = 2 \\ x = - 2 \end{matrix} \end{aligned}$

Vậy $x = 3, x = 2, x = - 2$

Bài 56 trang 24 sgk Toán 8 Tập 1: Tính nhanh giá trị của đa thức:

a) $x^{2} + \frac{1}{2} x + \frac{1}{16}$ tại $x = 49, 75$ ;

b) $x^{2} - y^{2} - 2 y - 1$ tại $x = 93$ và $y = 6$ .

Phương pháp giải: Phân tích các đa thức đó thành nhân tử bằng phương pháp dùng hằng đẳng thức rồi thay các giá trị tương ứng của $x, y$ để tính giá trị của đa thức đó.

Lời giải:

$x^{2} + \frac{1}{2} x + \frac{1}{16}$ tại $x = 49, 75$

Ta có: $x^{2} + \frac{1}{2} x + \frac{1}{16}$

$= x^{2} + 2 . x . \frac{1}{4} + {(\frac{1}{4})}^{2}$

$= {(x + \frac{1}{4})}^{2}$

Với $x = 49, 75$ ta có: ${(49, 75 + \frac{1}{4})}^{2} = (49, 75 + 0, 25)^{2}$ $= 50^{2} = 2500$

$x^{2} - y^{2} - 2 y - 1$ tại $x = 93$ và $y = 6$

Ta có: $x^{2} - y^{2} - 2 y - 1$

$= x^{2} + (- y^{2} - 2 y - 1)$

$= x^{2} - (y^{2} + 2 y + 1)$

$= x^{2} - {(y + 1)}^{2}$

$= [x - (y + 1)] . [x + (y + 1)]$

$= (x - y - 1) (x + y + 1)$

Với $x = 93, y = 6$ ta được:

$(93 - 6 - 1) (93 + 6 + 1) = 86.100$ $= 8600$

Bài 57 trang 24 sgk Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) $x^{2} - 4 x + 3$ ;

b) $x^{2} + 5 x + 4$ ;

c) $x^{2} - x - 6$ ;

d) $x^{4} + 4$

Phương pháp giải: Áp dụng các phương pháp: nhóm, tách, thêm bớt để xuất hiện nhân tử chung.

Tách: $- 4 x = - x - 3 x$

Lời giải:

$\begin{aligned} x^{2} - 4 x + 3 = x^{2} - x - 3 x + 3 \\ = (x^{2} - x) + (- 3 x + 3) \\ = x (x - 1) - 3 (x - 1) \\ = (x - 1) (x - 3) \end{aligned}$

Cách 2:

$\begin{array}{l} x^{2} - 4 x + 3 \\ = x^{2} - 4 x + 4 - 4 + 3 \\ = (x^{2} - 4 x + 4) - 1 \\ = (x^{2} - 2. x .2 + 2^{2}) - 1 \\ = {(x - 2)}^{2} - 1^{2} \\ = (x - 2 + 1) (x - 2 - 1) \\ = (x - 1) (x - 3) \end{array}$

$\begin{aligned} x^{2} + 5 x + 4 = x^{2} + 4 x + x + 4 \\ = (x^{2} + 4 x) + (x + 4) \\ = x (x + 4) + (x + 4) \\ = (x + 4) (x + 1) \end{aligned}$

$\begin{aligned} x^{2} - x - 6 = x^{2} + 2 x - 3 x - 6 \\ = (x^{2} + 2 x) + (- 3 x - 6) \\ = x (x + 2) - 3 (x + 2) \\ = (x + 2) (x - 3) \end{aligned}$

$\begin{aligned} x^{4} + 4 = x^{4} + 4 x^{2} + 4 - 4 x^{2} \\ = (x^{4} + 4 x^{2} + 4) - 4 x^{2} \\ = [{(x^{2})}^{2} + 2. x^{2} .2 + 2^{2}] - 4 x^{2} \\ = (x^{2} + 2)^{2} - {(2 x)}^{2} \\ = (x^{2} + 2 - 2 x) (x^{2} + 2 + 2 x) \end{aligned}$

Bài 58 trang 24 sgk Toán 8 Tập 1: Chứng minh rằng $n^{3} - n$ chia hết cho $6$ với mọi số nguyên $n .$

Phương pháp giải: Phân tích đa thức đã cho thành nhân tử, sau đó áp dụng tính chất: Một số chia hết cho $2$ và $3$ thì số đó chia hết cho $6.$

Lời giải:

Ta có: $n^{3} - n = n (n^{2} - 1) = n (n - 1) (n + 1)$

Với $n \in Z$ thì $(n - 1), n, (n + 1)$ là ba số nguyên liên tiếp.

+) Trong 3 số nguyên liên tiếp sẽ có ít nhất 1 số chẵn nên $n (n - 1) (n + 1)$ chia hết cho $2$

+) Trong 3 số nguyên liên tiếp sẽ có 1 số chia hết cho 3 nên $n (n - 1) (n + 1)$ chia hết cho $3$

Do đó tích $n (n - 1) (n + 1)$ chia hết cho cả $2$ và $3$ .

Mà $2$ và $3$ là hai số nguyên tố cùng nhau nên tích đó chia hết cho $6$ hay $n^{3} - n$ chia hết cho $6$ với mọi số nguyên $n .$

Lý thuyết Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp

I. Các kiến thức cần nhớ: Ngoài các phương pháp đặt nhân tử chung, dùng hằng đẳng thức, nhóm nhiều hạng tử để phân tích đa thức thành nhân tử , ta còn sử dụng các cách sau:

a. Tách một hạng tử thành nhiều hạng tử

Ví dụ: $x^{2} + 3 x + 2 = x^{2} + x + 2 x + 2 = x (x + 1) + 2 (x + 1) = (x + 1) (x + 2)$

Một cách tổng quát: Để phân tích tam thức bậc hai $a x^{2} + b x + c$ thành nhân tử

Ta tách hạng tử $b x$ thành $b_{1} x + b_{2} x$ sao cho , tức là $b_{1} b_{2} = a c .$

Trong khi làm bài ta thực hiện các bước như sau:

-Bước $1$ : Tìm tích $a . c$

-Bước $2$ : Phân tích tích $a . c$ ra tích của hai thừa số nguyên tố bằng mọi cách.

-Bước $3$ : Chọn hai thừa số mà tổng bằng $b .$

b. Thêm bớt cùng một hạng tử

- Thêm bớt cùng một hạng tử để xuất hiện hiệu hai bình phương.

Ví dụ: $x^{4} + 4 = {(x^{2})}^{2} + 4 x^{2} + 4 - 4 x^{2}$

$= {(x^{2} + 2)}^{2} - {(2 x)}^{2}$ $= (x^{2} + 2 x + 2) (x^{2} - 2 x + 2)$

- Thêm bớt cùng một hạng tử để xuất hiện nhân tử chung.

Ví dụ $: x^{5} + x^{4} + 1$ $= (x^{5} + x^{4} + x^{3}) - (x^{3} - 1)$ $= x^{3} (x^{2} + x + 1) - (x - 1) (x^{2} + x + 1)$

$= (x^{2} + x + 1) (x^{3} - x + 1)$

c. Đặt ẩn phụ

Ví dụ: $(x^{2} + 2 x) (x^{2} + 2 x + 4) + 3$

Đặt $x^{2} + 2 x = t$ , đa thức trên trở thành:

$t (t + 4) + 3$ $= t^{2} + 4 t + 3$ $= t^{2} + t + 3 t + 3$ $= t (t + 1) + 3 (t + 1)$ $= (t + 1) (t + 3)$

Thay $t = x^{2} + 2 x$ , ta được: $(x^{2} + 2 x) (x^{2} + 2 x + 4) + 3$ $= (x^{2} + 2 x + 1) (x^{2} + 2 x + 3) .$

d. Phối hợp nhiều phương pháp

Để phân tích một đa thức thành nhân tử ta có thể kết hợp nhiều phương pháp trên với nhau.

Ví dụ: $x^{2} - 2 y z - y^{2} - z^{2}$ $= x^{2} - (y^{2} + 2 y z + z^{2})$ $= x^{2} - {(y + z)}^{2}$ $= (x + y + z) (x - y - z)$

Ở ví dụ trên ta đã kết hợp phương pháp nhóm hạng tử và hằng đẳng thức để phân tích đa thức thành nhân tử.

Nếu các hạng tử của đa thức có nhân tử chung thì ta nên đặt nhân tử chung ra ngoài dấu ngoặc để đa thức trong ngoặc đơn giản hơn rồi mới tiếp tục phân tích đến kết quả cuối cùng.

II. Các dạng toán thường gặp:

Dạng 1: Phân tích đa thức thành nhân tử

Phương pháp: Sử dụng các phương pháp đã học để phân tích đa thức thành nhân tử.

Dạng 2: Tìm $x$ .

Phương pháp: Sử dụng các phương pháp đã học để phân tích đa thức thành nhân tử.

Từ đó biến đổi về dạng tìm $x$ thường gặp.

Chẳng hạn $A . B = 0 \Leftrightarrow [\begin{array}{l} A = 0 \\ B = 0 \end{array}$