Với giải sách bài tập Toán 10 Bài tập cuối chương 7 sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải SBT Toán lớp 10 Bài tập cuối chương 7

Giải SBT Toán 10 trang 19 Tập 2

A. TRẮC NGHIỆM

Câu 1 trang 19 SBT Toán 10 Tập 2: Tam thức bậc hai nào có biệt thức ∆ = 1 và hai nghiệm là: $x_1=\frac{3}{2}$ và $x_2=\frac{7}{4}?$

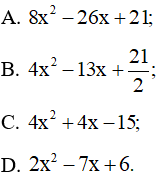
Lời giải:

Đáp án đúng là B

Sử dụng máy tính cầm tay ta tính được các tam thức bậc hai f ( x ) = $8x^2-26x+21$ và g ( x ) = $4x^2-13x+\frac{21}{2}$ đều có hai nghiệm phân biệt $x_1=\frac{3}{2}$và $x_2=\frac{7}{4}$.

Xét f ( x ): ∆ = (–26)² – 4.8.21 = 4

Xét g ( x ): ∆ = (–13)² – 4.4.$\frac{21}{2}$ = 1

Vậy đáp án đúng là B.

Câu 2 trang 19 SBT Toán 10 Tập 2: Tam thức bậc hai nào dương với mọi $x\in ℝ$?

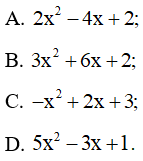
Lời giải:

Đáp án đúng là D

+) Ta có f ( x ) = $2x^2-4x+2$ = 2(x – 1)² > 0 với mọi x ≠ 1. Do đó A sai.

+) Tam thức bậc hai f (x) = $2x^2-4x+2$ có hai nghiệm phân biệt x₁ = $\frac{-3+\sqrt{3}}{3}$ và

x₂ = $\frac{-3-\sqrt{3}}{3}$, a = 3 > 0 nên f ( x ) > 0 khi x < $\frac{-3-\sqrt{3}}{3}$ hoặc x > $\frac{-3+\sqrt{3}}{3}$. Do đó B sai.

+) Tam thức bậc hai f ( x ) = $-x^2+2x+3$ có hai nghiệm phân biệt x₁ = 3 và x₂ = –1,

a = –1 < 0 nên f ( x ) > 0 khi – 1 < x < 3. Do đó C sai.

+) Tam thức bậc hai f ( x ) = $-x^2+2x+3$ có ∆ = ( –3)² – 4.5.1 = –11 < 0, a = 5 > 0 nên f ( x ) > 0 với mọi $x\in ℝ$. Do đó D đúng.

Vậy đáp án D đúng.

Câu 3 trang 19 SBT Toán 10 Tập 2: Khẳng định nào sau đây đúng với tam thức bậc hai $f\left(x\right)=10x^2-3x-4?$

A. f(x) > 0 với mọi x không thuộc khoảng (-1; 1),

B. f(x) < 0 với mọi x thuộc khoảng (-1; 1),

C. $f\left(x\right)\ge 0$ với mọi x thuộc khoảng $\left(-\frac{1}{2};\frac{4}{5}\right)$

D. Các khẳng định trên đều sai.

Lời giải:

Đáp án đúng là D

Tam thức bậc hai $f\left(x\right)=10x^2-3x-4$ có hai nghiệm phân biệt x₁ = $\frac{4}{5}$ và x₂ = $\frac{-1}{2}$, và a = 10 > 0 nên:

f ( x ) > 0 với x < $\frac{-1}{2}$ hoặc x > $\frac{4}{5}$. Do đó khẳng định A sai.

f ( x ) < 0 với $\frac{-1}{2}$ < x < $\frac{4}{5}$. Do đó khẳng định B sai.

f ( x ) ≥ 0 với x ≤ $\frac{-1}{2}$ hoặc x ≥ $\frac{4}{5}$. Do đó khẳng định C sai.

Vậy khẳng định D đúng.

Câu 4 trang 19 SBT Toán 10 Tập 2: Trong trường hợp nào tam thức bậc hai f(x) = ax² + bx + c có $\Delta >0$ và a < 0?

A.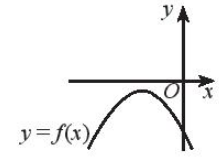 

B.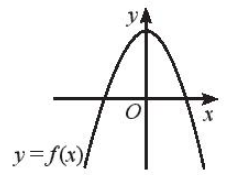 

C.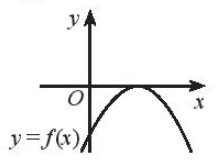 

D.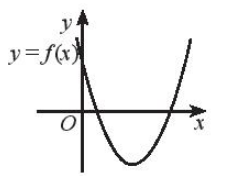 

Lời giải:

Đáp án đúng là B

Tam thức bậc hai $f\left(x\right){\text{=ax}}^2+bx+c$ có $\Delta >0$ và a < 0 khi f ( x ) cắt trục hoành tại hai điểm phân biệt và đường cong hướng xuống dưới. Do đó B đúng.

Giải SBT Toán 10 trang 20 Tập 2

Câu 5 trang 20 SBT Toán 10 Tập 2: Cho đồ thị của hàm số bậc hai y = f(x) như Hình 1.

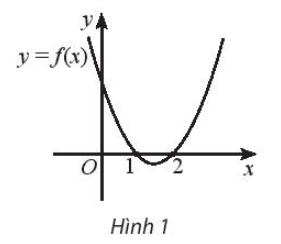
Tập nghiệm của bất phương trình $f\left(x\right)\ge 0$ là:

A. $\left(1;2\right)$;

B. $\left[1;2\right]$;

C. $\left(-\infty ;1\right)\cup \left(2;+\infty \right)$;

D. $\left(-\infty ;1\right]\cup \left[2;+\infty \right)$.

Lời giải:

Đáp án đúng là D

Tập nghiệm của bất phương trình $f\left(x\right)\ge 0$ là $\left(-\infty ;1\right]\cup \left[2;+\infty \right)$.

Câu 6 trang 20 SBT Toán 10 Tập 2: Bất phương trình nào có tập nghiệm là (2; 5)?

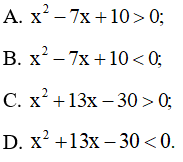
Lời giải:

Đáp án đúng là B

+) Tam thức bậc hai f ( x ) = x² – 7x +10 có ∆ = ( – 7)² – 4.1.10 = 9 > 0 nên f(x) có hai nghiệm phân biệt x₁ = 2 và x₂ = 5, và a = 1 > 0 nên ta có:

f ( x ) > 0 với x < 2 hoặc x > 5.

f ( x ) < 0 với 2 < x < 5.

Do đó A sai, B đúng.

+) Tam thức bậc hai f ( x ) = $x^2+13x-30$ có ∆ = 13² – 4.1.(– 30) = 289 > 0 nên f(x) hai nghiệm phân biệt x₁ = 2 và x₂ = –15, và a = 1 > 0 nên ta có:

f ( x ) > 0 với x < –15 hoặc x > 2.

f ( x ) < 0 với –15 < x < 2.

Do đó C, D sai.

Vậy đáp án đúng là B.

Câu 7 trang 20 SBT Toán 10 Tập 2: Tập xác định của hàm số$y=\frac{1}{\sqrt{9x^2-3x-2}}+\sqrt{3-x}$ là:

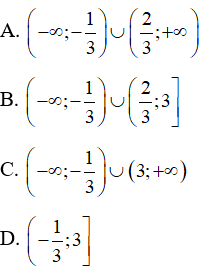
Lời giải:

Đáp án đúng là B

Hàm số trên xác định khi và chỉ khi 3 – x ≥ 0 và 9x² – 3x – 2 > 0

+) Ta có 3 – x ≥ 0 khi và chỉ khi x ≤ 3 (1)

+) Xét tam thức bậc hai f ( x ) = 9x² – 3x – 2 có ∆ = (– 3)² – 4.9.(– 2) = 81 > 0 nên f(x) có hai nghiệm phân biệt x₁ = $\frac{2}{3}$ và x₂ = $\frac{-1}{3}$, và a = 9 > 0 nên f ( x ) > 0 với $\left(-\infty ;\frac{-1}{3}\right)\cup \left(\frac{2}{3};+\infty \right)$ (2)

Từ (1) và (2) suy ra tập xác định của hàm số trên là $\left(-\infty ;-\frac{1}{3}\right)\cup \left(\frac{2}{3};3\right]$.

Vậy đáp án đúng là B.

Câu 8 trang 20 SBT Toán 10 Tập 2: Với giá trị nào của tham số m thì phương trình $\left(2m+6\right)x^2+4mx+3=0$có hai nghiệm phân biệt?

A. $m<-\frac{3}{2}$ hoặc m > 3;

B. $-\frac{3}{2}<m<3;$

C. m < - 3  hoặc $-3<m<-\frac{3}{2}$ hoặc m > 3;

D. $-3<m<-\frac{3}{2}$ hoặc m > 3.

Lời giải:

Đáp án đúng là A

+) 2m + 6 = 0 ⇔ m = –3, khi đó phương trình trở thành –12x + 3 = 0 ⇒ x = $\frac{1}{4}$. Suy ra phương trình chỉ có một nghiệm duy nhất. Do đó không thỏa mãn.

+) 2m + 6 ≠ 0 ⇔ m ≠ –3

Khi đó phương trình $\left(2m+6\right)x^2+4mx+3=0$có hai nghiệm phân biệt khi và chỉ khi

∆ = (4m)² – 4.3.(2m + 6) > 0 hay 2m² – 3m – 9 > 0

Tam thức bậc hai f ( x ) = 2m² – 3m – 9 có hai nghiệm phân biệt x₁ = 3 và x₂ = $\frac{-3}{2}$,

a = 2 > 0 nên f ( x ) > 0 với x < $\frac{-3}{2}$ hoặc x > 3 (2)

Từ điều kiện (1) và (2) suy ra m < - 3  hoặc $-3<m<-\frac{3}{2}$ hoặc m > 3.

Vậy đáp án đúng là C.

Câu 9 trang 20 SBT Toán 10 Tập 2: Giá trị nào là nghiệm của phương trình $\sqrt{x^2+x+11}=\sqrt{-2x^2-13x+16}?$

A. x = – 5

B. $x=\frac{1}{3}$

C. Cả hai câu A, B đều đúng;

D. Cả hai câu A, B đều sai.

Lời giải:

Đáp án đúng là C

Bình phương hai vế của phương trình đã cho, ta được:

x² + x + 11 = –2x² – 13x + 16

⇒ 3x² + 14x – 5 = 0

⇒ x = $\frac{1}{3}$ hoặc x = –5.

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy x = $\frac{1}{3}$ hoặc x = –5 đều thỏa mãn.

Vì vậy phương trình đã cho có hai nghiệm x = $\frac{1}{3}$ và x = –5

Vậy đáp án đúng là C.

Câu 10 trang 20 SBT Toán 10 Tập 2: Khẳng định nào đúng với phương trình $\sqrt{2x^2-3x-1}=\sqrt{3x^2-2x-13}?$

A. Phương trình có hai nghiệm phân biệt cùng dấu;

B. Phương trình có hai nghiệm phân biệt trái dấu;

C. Phương trình có một nghiệm;

D. Phương trinh vô nghiệm.

Lời giải:

Đáp án đúng là B

Bình phương hai vế của phương trình đã cho, ta được:

2x² – 3x – 1 = 3x² – 2x – 13

⇒ x² + x – 12 = 0

⇒ x = 3 hoặc x = –4.

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy x = 3 hoặc x = –4 đều thỏa mãn.

Suy ra phương trình đã cho có hai nghiệm x = 3 và x = –4. Vậy hai nghiệm của phương trình đã cho là hai nghiệm phân biệt trái dấu.

Đáp án đúng là B.

Câu 11 trang 20 SBT Toán 10 Tập 2: Khẳng định nào đúng với phương trình $\sqrt{5x^2+27x+36}=2x+5?$

A. Phương trình có một nghiệm;

B. Phương trình vô nghiệm;

C. Tổng các nghiệm của phương trình là -7;

D. Các nghiệm của phương trình đều không bé hơn $\frac{-5}{2}$.

Lời giải:

Đáp án đúng là A

Bình phương hai vế của phương trình đã cho, ta được:

5x² + 27x + 36 = 4x² + 20x + 25

⇒ x² + 7x + 11 = 0

⇒ x = $\frac{-7+\sqrt{5}}{2}$ hoặc x = $\frac{-7-\sqrt{5}}{2}$.

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy chỉ có x = $\frac{-7+\sqrt{5}}{2}$ thỏa mãn.

Vì vậy đáp án A đúng.

Câu 12 trang 20 SBT Toán 10 Tập 2: Cho đồ thị của hai hàm số bậc hai f(x) = ax² + bx + c và g(x) = dx² + ex + h như Hình 2.

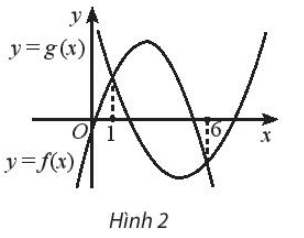
Khẳng định nào đúng với phương trình $\sqrt{{\text{ax}}^2+bx+c}=\sqrt{d{x}^2+\text{ex}+h}?$

A. Phương trình có hai nghiệm phân biệt là x = 1 và x = 6,

B. Phương trình có 1 nghiệm là x = l;

C. Phương trình có 1 nghiệm là x = 6;

D. Phương trình vô nghiệm.

Lời giải:

Đáp án đúng là B

Xét phương trình $\sqrt{{\text{ax}}^2+bx+c}=\sqrt{d{x}^2+\text{ex}+h}$

Bình phương hai vế ta được f ( x ) = g ( x )

Đồ thị hàm số f ( x ) và g ( x ) giao nhau tại hai điểm x = 1 và x = 6. Tuy nhiên tại

x = 6 thì g ( x ) < 0 và f ( x ) < 0 nên không thỏa mãn.

Vậy phương trình có 1 nghiệm là x = 1.

B. TỰ LUẬN

Giải SBT Toán 10 trang 21 Tập 2

Bài 1 trang 21 SBT Toán 10 Tập 2: Dựa vào đồ thị của hàm số bậc hai $y=f\left(x\right)$sau đây, hãy xét dấu của tam thức bậc hai f(x).

a)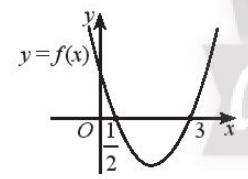 

b)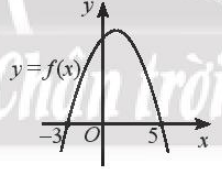 

c)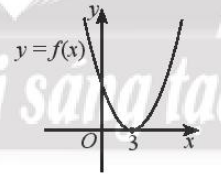 

d)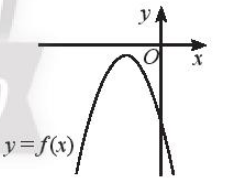 

Lời giải:

a) Dựa vào hình vẽ ta thấy:

Đồ thị hàm số nằm phía trên trục hoành khi x < $\frac{1}{2}$ hoặc x > 3 hay f(x) > 0 khi x ∈ $\left(-\infty ;\frac{1}{2}\right)$ ∪ (3; +∞).

Đồ thị hàm số nằm phía dưới trục hoành khi $\frac{1}{2}<x<3$ hay f(x) < 0 khi x ∈ $\left(\frac{1}{2};3\right)$

Vậy f ( x ) dương trong hai khoảng $\left(-\infty ;\frac{1}{2}\right)$ và (3; +∞), f(x) âm khi x ∈ $\left(\frac{1}{2};3\right)$.

b) Dựa vào hình vẽ ta thấy:

Đồ thị hàm số nằm phía trên trục hoành khi  –3 < x < 5 hay f(x) > 0 khi x ∈ (–3; 5)

Đồ thị hàm số nằm phía dưới trục hoành khi x < –3 hoặc x > 5 hay f(x) < 0 khi x ∈ $\left(-\infty ;-3\right)$ ∪ (5; +∞)

Vậy f ( x ) dương trong khoảng ( –3; 5 ), âm trong hai khoảng $\left(-\infty ;-3\right)$ và $\left(5;+\infty \right)$.

c) Đồ thị hàm số nằm phía trên trục hoành khi x ≠ 3.

Vậy f ( x ) dương với mọi x ≠ 3.

d) Đồ thị hàm số nằm phía dưới trục hoành với mọi x ∈ ℝ.

Vậy f ( x ) âm với mọi x ∈ ℝ.

Bài 2 trang 21 SBT Toán 10 Tập 2: Xét dấu của các tam thức bậc hai sau:

Ý b

Ý c

Ý d

Ý e

Ý g

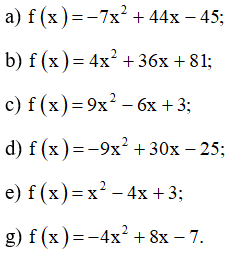
Lời giải:

a) Tam thức bậc hai $f\left(x\right)=-7x^2+44x-45$ có ∆ = 44² – 4.(– 7).(– 45) = 676 > 0 suy ra f(x) có hai nghiệm phân biệt x₁ = 5 và x₂ = $\frac{9}{7}$, a = –7 < 0 nên f ( x ) dương trong khoảng $\left(\frac{9}{7};5\right)$, âm trong hai khoảng $\left(-\infty ;\frac{9}{7}\right)$ và $\left(5;+\infty \right)$.

b) Tam thức bậc hai $f\left(x\right)=4x^2+36x+81$ có ∆ = 36² – 4.4.81 = 0 suy ra f(x) có một nghiệm duy nhất x = $\frac{-9}{2}$ , a = 4 > 0 nên f ( x ) dương với mọi x ≠ $\frac{-9}{2}$.

c) Tam thức bậc hai $f\left(x\right)=9x^2-6x+3$ có ∆ = ( –6 )² – 4.9.3 = –72 < 0 và a = 9 > 0 nên f ( x ) dương với mọi x ∈ ℝ.

d) Tam thức bậc hai $f\left(x\right)=-9x^2+30x-25$ có ∆ = 30² – 4.( –9).( –25) = 0 suy ra f(x) có một nghiệm duy nhất x = $\frac{5}{3}$ , a = –9 < 0 nên f ( x ) âm với mọi x ≠ $\frac{5}{3}$.

e) Tam thức bậc hai $f\left(x\right)=x^2-4x+3$ có ∆ = (–4)² – 4.1.3 = 4 suy ra f(x) có hai nghiệm phân biệt x₁ = 3 và x₂ =1, a = 1 > 0 nên

f ( x ) âm trong khoảng $\left(1;3\right)$, f(x) dương trong hai khoảng $\left(-\infty ;1\right)$ và $\left(3;+\infty \right)$.

g) Tam thức bậc hai $f\left(x\right)=-4x^2+8x-7$ có ∆ = 8² – 4.( –4).( –7) = –48 < 0 ,

a = –4 < 0 nên f ( x ) âm với mọi x ∈ ℝ.

Bài 3 trang 21 SBT Toán 10 Tập 2: Giải các bất phương trình bậc hai sau:

Ý b

Ý c

Ý d

Ý e

Ý g

Ý h

Ý i

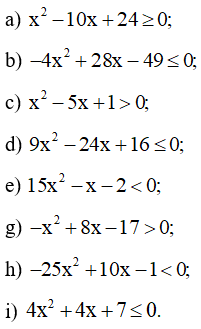
Lời giải:

a) $x^2-10x+24\ge 0;$

Tam thức bậc hai f ( x ) = x² – 10x + 24 có ∆ = (– 10)² – 4.1.24 = 4 > 0 suy ra f(x) có hai nghiệm phân biệt x₁ = 6 và x₂ = 4 và a = 1 > 0 nên f ( x ) > 0 với x ≤ 4 hoặc x ≥ 6.

Vậy bất phương trình đã cho có tập nghiệm S = (– ∞; 4] ∪ [6; +∞)

b) $-4x^2+28x-49\le 0;$

Tam thức bậc hai f ( x ) = –4x² + 28x – 49 có ∆ = 28² – 4.(– 4).(– 49) = 0 suy ra f(x) có một nghiệm x = $\frac{7}{2}$ , a = –4 < 0 nên f ( x ) ≤  0 với mọi x ∈ ℝ.

Vậy bất phương trình đã cho có tập nghiệm S = ℝ.

c) $x^2-5x+1>0;$

Tam thức bậc hai f ( x ) = x² – 5x + 1 có ∆ = (–5)² – 4.1.1 = 21 suy ra f(x) có hai nghiệm phân biệt x₁ = $\frac{5+\sqrt{21}}{2}$ và x₂ = $\frac{5-\sqrt{21}}{2}$, a = 1 > 0 nên f ( x ) > 0 với x < $\frac{5-\sqrt{21}}{2}$ hoặc x > $\frac{5+\sqrt{21}}{2}$.

Vậy bất phương trình đã cho có tập nghiệm S = $\left(-\infty ;\frac{5-\sqrt{21}}{2}\right)\cup \left(\frac{5+\sqrt{21}}{2};+\infty \right)$

d) $9x^2-24x+16\le 0;$

Tam thức bậc hai f ( x ) = 9x² – 24x +16 có ∆ = (–24)² – 4.9.16 = 0 suy ra f(x) có một nghiệm x = $\frac{4}{3}$ , a = 9 > 0 nên f ( x ) ≤  0 khi x = $\frac{4}{3}$.

Vậy bất phương trình đã cho có tập nghiệm S = $\left\{\frac{4}{3}\right\}$

e) $15x^2-x-2<0;$

Tam thức bậc hai f ( x ) = 15x² – x – 2 có ∆ = (–1)² – 4.15.( –2) = 121 suy ra f(x) có hai nghiệm phân biệt x₁ = $\frac{2}{5}$ và x₂ = $\frac{-1}{3}$, a = 15 > 0 nên f ( x ) < 0 với $\frac{-1}{3}$ < x < $\frac{2}{5}$.

Vậy bất phương trình đã cho có tập nghiệm S = $\left(\frac{-1}{3};\frac{2}{5}\right)$

g) $-x^2+8x-17>0;$

Tam thức bậc hai f ( x ) = –x² + 8x – 17 có ∆ = 8² – 4.( –1).( –17) = –4 < 0 , a = –1 < 0 nên f ( x ) âm với mọi x ∈ ℝ.

Vậy bất phương trình vô nghiệm.

h) $-25x^2+10x-1<0;$

Tam thức bậc hai f ( x ) = –25x² + 10x – 1 có ∆ = 10² – 4.( –25).( –1) = 0  suy ra f(x) có một nghiệm x = $\frac{1}{5}$ , a = –25 < 0 nên f ( x ) < 0 khi x ≠ $\frac{1}{5}$.

Vậy bất phương trình đã cho có tập nghiệm S = ℝ \ $\frac{1}{5}$.

i) $4x^2+4x+7\le 0.$

Tam thức bậc hai f ( x ) = 4x² + 4x + 7 có ∆ = 4² – 4.4.7 = –96 < 0 , a = 4 > 0 nên f ( x ) dương với mọi x ∈ ℝ.

Vậy bất phương trình vô nghiệm.

Giải SBT Toán 10 trang 22 Tập 2

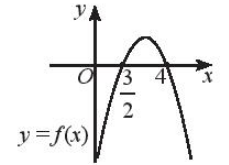
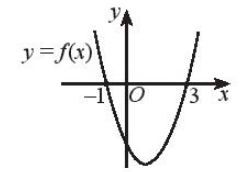
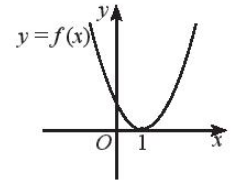
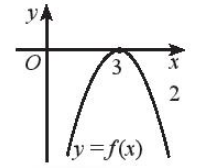
Bài 4 trang 22 SBT Toán 10 Tập 2: Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải các bất phương trình sau:

a) $f\left(x\right)\ge 0$

b) $f\left(x\right)>0$

c) $f\left(x\right)\le 0$

d) $f\left(x\right)<0$

 

 

 

e) $f\left(x\right)<0$

g) $f\left(x\right)\le 0$

Lời giải:

a) Ta thấy đồ thị hàm số f ( x ) cắt trục hoành tại hai điểm x = $\frac{3}{2}$ và x = 4, khi $\frac{3}{2}$ ≤ x ≤ 4 thì đồ thị hàm số nằm trên trục hoành nên $f\left(x\right)\ge 0$ khi $\frac{3}{2}$ ≤ x ≤ 4.

Vậy f(x) ≥ 0 khi x ∈ $\left[\frac{3}{2};4\right]$.

b) $f\left(x\right)>0$ khi đồ thị hàm số f ( x ) nằm trên trục hoành hay x < –1 hoặc x > 3.

Vậy f(x) > 0 khi (– ∞; – 1) ∪ (3; +∞).

c) Dựa vào hình vẽ ta thấy:

Đồ thị hàm số cắt trục hoành tại x = 1.

Với x ≠ 1 đồ thị hàm số nằm hoàn toàn phía trên trục hoành.

Do đó f(x) ≤ 0 khi x = 1.

Vậy f(x) ≤ 0 khi x = 1.

d) $f\left(x\right)<0$ vô nghiệm vì ta thấy đồ thị hàm số f ( x ) hoàn toàn nằm trên trục hoành.

Vậy không tồn tại giá trị của x để f(x) < 0.

e) Dựa vào hình vẽ ta thấy:

Đồ thị hàm số cắt trục hoành tại x = 3.

Đồ thị nằm hoàn toàn phía dưới trục hoành với x ≠ 3.

Do đó $f\left(x\right)<0$ khi x ≠ 3.

Vậy f(x) < 0 khi x ≠ 3.

g) Ta có thể thấy đồ thị hàm số f ( x ) hoàn toàn nằm dưới trục hoành nên $f\left(x\right)\le 0$ với mọi x ∈ ℝ.

Vậy f(x) ≤ 0 với mọi x ∈ ℝ.

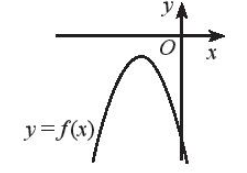
Bài 5 trang 22 SBT Toán 10 Tập 2: Giải các phương trình sau:

Ý b

Ý c

Ý d

Ý e

Ý g

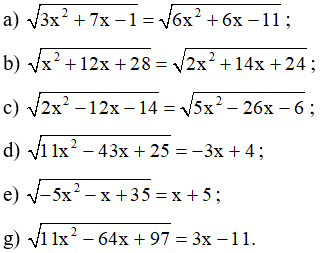
Lời giải:

a) $\sqrt{3x^2+7x-1}=\sqrt{6x^2+6x-11}$

Bình phương hai vế của phương trình đã cho, ta được:

3x² + 7x – 1 = 6x² + 6x – 11

⇒ 3x² – x – 10 = 0

⇒ x = $\frac{-5}{3}$ hoặc x = 2.

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy chỉ có x = 2 thỏa mãn. Vậy phương trình đã cho có nghiệm x = 2.

b) $\sqrt{x^2+12x+28}=\sqrt{2x^2+14x+24}$

Bình phương hai vế của phương trình đã cho, ta được:

x² + 12x + 28 = 2x² + 14x + 24

⇒ x² + 2x – 4 = 0

⇒ x = –1 + $\sqrt{5}$ hoặc x = –1 – $\sqrt{5}$.

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy chỉ có x = –1 + $\sqrt{5}$ thỏa mãn.

Vậy phương trình đã cho có nghiệm x = –1 + $\sqrt{5}$.

c) $\sqrt{2x^2-12x-14}=\sqrt{5x^2-26x-6}$

Bình phương hai vế của phương trình đã cho, ta được:

2x² – 12x – 14 = 5x² – 26x – 6

⇒ 3x² – 14x + 8 = 0

⇒ x = 4 hoặc x = $\frac{2}{3}$

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy x = 4 và x = $\frac{2}{3}$ đều không thỏa mãn. Vậy phương trình đã cho vô nghiệm.

d) $\sqrt{11x^2-43x+25}=-3x+4$

Bình phương hai vế của phương trình đã cho, ta được:

11x² – 43x + 25 = 9x² – 24x + 16

⇒ 2x² – 19x + 9 = 0

⇒ x = 9 hoặc x = $\frac{1}{2}$

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy chỉ có x = $\frac{1}{2}$ thỏa mãn. Vậy phương trình đã cho có nghiệm x = $\frac{1}{2}$.

e) $\sqrt{-5x^2-x+35}=x+5$

Bình phương hai vế của phương trình đã cho, ta được:

–5x² – x + 35 = x² + 10x + 25

⇒ 6x² + 11x – 10 = 0

⇒ x = $\frac{2}{3}$ hoặc x = $\frac{-5}{2}$

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy x = $\frac{2}{3}$ hoặc x = $\frac{-5}{2}$ đều thỏa mãn.

Vậy phương trình đã cho có nghiệm x = $\frac{2}{3}$ và x = $\frac{-5}{2}$.

g) $\sqrt{11x^2-64x+97}=3x-11.$

Bình phương hai vế của phương trình đã cho, ta được:

11x² – 64x + 97 = 9x² – 66x + 121

⇒ 2x² + 2x – 24 = 0

⇒ x = 3 hoặc x = –4

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy x = 3 và x = –4

đều không thỏa mãn.

Vậy phương trình đã cho vô nghiệm.

Bài 6 trang 22 SBT Toán 10 Tập 2: Tìm tập xác định của các hàm số sau:

a) $y=\sqrt{-x^2+6x-2};$

b) $y=\frac{2x}{x-2}+\sqrt{-x^2+3x-2}$

Lời giải:

a) $y=\sqrt{-x^2+6x-2};$

Hàm số trên xác định khi và chỉ khi –x² + 6x – 2 ≥ 0

Tam thức bậc hai f ( x ) = –x² + 6x – 2 có hai nghiệm phân biệt x₁ = 3 +$\sqrt{7}$ và

x₂ = 3 – $\sqrt{7}$, a = –1 < 0 nên f ( x ) ≥ 0 khi 3 – $\sqrt{7}$ ≤ x ≤ 3 +$\sqrt{7}$.

Vậy tập xác định của hàm số trên là D = $\left[3-\sqrt{7};3+\sqrt{7}\right]$.

b) $y=\frac{2x}{x-2}+\sqrt{-x^2+3x-2}$

Hàm số trên xác định khi và chỉ khi x – 2 ≠ 0 và –x² + 3x –2 ≥ 0.

+) Ta có x – 2 ≠ 0 khi và chỉ khi x ≠ 2 (1)

+)Tam thức bậc hai f ( x ) = –x² + 3x –2 có hai nghiệm phân biệt x₁ = 1 và x₂ = 2,

a = –1 < 0 nên f ( x ) ≥ 0 khi 1 ≤ x ≤ 2 (2)

Từ (1) và (2) suy ra tập xác định của hàm số là $\left[1;2\right)$.

Vậy tập xác định của hàm số là D = $\left[1;2\right)$.

Bài 7 trang 22 SBT Toán 10 Tập 2: Tìm các giá trị của tham số m để:

a) $f\left(x\right)=\left(m-3\right)x^2+2mx-m$ là một tam thức bậc hai âm với mọi $x\in ℝ$;

b) $f\left(x\right)=\left(m-2\right)x^2+2\left(m+3\right)x+5\left(m-3\right)$ là một tam thức bậc hai có nghiệm;

c) Phương trình $2x^2+\left(3m-1\right)x+2\left(m+1\right)=0$ vô nghiệm,

d) Bất phương trình $2x^2+2\left(m-3\right)x+3\left(m^2-3\right)\ge 0$ có tập nghiệm là $ℝ$.

Lời giải:

a) f ( x ) là một tam thức bậc hai âm với mọi x ∈ ℝ khi và chỉ khi a = m – 3 < 0 và

∆’ < 0.

+) Ta có: m – 3 < 0 khi và chỉ khi m < 3.

+) ∆’ = m² + (m – 3).m = 2m² – 3m < 0 khi và chỉ khi 0 < m < $\frac{3}{2}$

Vậy để $f\left(x\right)=\left(m-3\right)x^2+2mx-m$ là một tam thức bậc hai âm với mọi x ∈ ℝ thì

0 < m < $\frac{3}{2}$.

b) f ( x ) là một tam thức bậc hai có nghiệm khi và chỉ khi m – 2 ≠ 0 và ∆’ ≥ 0.

+) Ta có m – 2 ≠ 0 khi và chỉ khi m ≠ 2

+) Ta có ∆’ = (m + 3)² – 5.(m – 3).(m – 2) = –4m² + 31m – 21 ≥  0 tức là

$\frac{3}{4}$ ≤ m ≤ 7.

Vậy $\frac{3}{4}$ ≤ m < 2 và 2 < m ≤ 7 thì f(x) là một tam thức bậc hai có nghiệm.

c) Phương trình vô nghiệm khi và chỉ khi

∆ = ( 3m – 1 )² – 16( m + 1 ) < 0 hay 9m² – 22m – 15 < 0 tức là $\frac{-5}{9}$< m < 3.

Vậy  $\frac{-5}{9}$< m < 3 thì phương trình đã cho vô nghiệm.

d) Xét tam thức bậc hai f(x) = 2x² + 2.(m – 3)x + 3(m² – 3) có a = 2 > 0 và ∆’ = ( m – 3 )² – 6( m² – 3 )  = m² – 6m + 9 – 6m² + 18 = – 5m² – 6m + 27

Suy ra f(x) ≥ 0 với mọi x ∈ ℝ khi a = 2 > 0 và ∆’ = –5m² – 6m + 27 ≤ 0 tức là m ≤ –3 hoặc m ≥ $\frac{9}{5}$.

Vậy m ≤ –3 hoặc m ≥ $\frac{9}{5}$.

Bài 8 trang 22 SBT Toán 10 Tập 2: Người ta thử nghiệm ném một quả bóng trên Mặt Trăng. Nếu quả bóng được ném lên từ độ cao h₀ (m) so với bề mặt của Mặt Trăng với vận tốc v₀ (m/s) thì độ cao của bóng sau t giây được cho bởi hàm số $h\left(t\right)=-\frac{1}{2}g{t}^2+v_{0}t+h_0$ với g = 1,625 m/s² là gia tốc trọng trường của Mặt Trăng.

a) Biết độ cao ban đầu của quả bóng vào các thời điểm 8 giây và 12 giây lần lượt là 30 m và 5 m, hãy tìm vận tốc ném; độ cao ban đầu của quả bóng và viết công thức h(t).

b) Quả bóng đạt độ cao trên 29 m trong bao nhiêu giây?

Lưu ý: Đáp số làm tròn đến hàng phần trăm.

Lời giải:

a) Ta có h ( t ) = –0,8125t² + v₀t + h₀

Ta có h(8) = 30 và h(12) = 5

Do đó $\left\{\begin{array}{l}-52+8{\text{v}}_{\text{0}}+{\text{h}}_{\text{0}}=30\\ -117+12{\text{v}}_{\text{0}}+{\text{h}}_{\text{0}}=5\end{array}\right.$ hay $\left\{\begin{array}{l}{\text{v}}_{\text{0}}=10\\ {\text{h}}_{\text{0}}=2\end{array}\right.$

Vậy h ( t ) = –0,8125t² + 10t + 2.

b) Quả bóng đạt độ cao trên 29 m khi và chỉ khi –0,8125t² + 10t + 2 > 29 hay

–0,8125t² + 10t – 27 > 0

Xét tam thức bậc hai f(t) = –0,8125t² + 10t – 27, có a = –0,8125 < 0 và ∆ = 10² – 4.(–0,8125).(– 27) = 12,25 > 0 suy ra f(t) có hai nghiệm phân biệt t₁ = 8,31 và 4.

Do đó f(t) > 0 khi 4 < t < 8,31.

Vậy quả bóng ở độ cao trên 29m trong khoảng ít hơn 8,31 – 4 = 4,31 giây.

Giải SBT Toán 10 trang 23 Tập 2

Bài 9 trang 23 SBT Toán 10 Tập 2: Một người phát cầu qua lưới từ độ cao y₀ mét, nghiêng một góc $\alpha$ so với phương ngang với vận tốc đầu v₀.

Phương trình chuyển động của quả cầu là:

$y=\frac{-g}{2v_0^2{\cos }^2\alpha }{x}^2+\tan \left(\alpha \right)x+y_0$ với g = 10 m/s²

a) Viết phương trình chuyển động của quả cầu nếu $\alpha ={45}^0,y_0=0,3m$ và v₀ = 7,67 m/s.

b) Để cầu qua được lưới bóng cao 1,5 m thì người phát cầu phải đứng cách lưới bao xa?

Lưu ý: Đáp số làm tròn đến hàng phần trăm.

Lời giải:

a) Ta có

$y=\frac{-g}{2v_0^2{\cos }^2\alpha }{x}^2+\tan \left(\alpha \right)x+y_0$

Thay $\alpha ={45}^0,y_0=0,3$ và v₀ = 7,67 vào phương trình trên ta được:

y = $\frac{-10}{2.7,{67}^2.{\cos }^{2}45°}$ + tan45°.x + 0,3 hay y = –0,17x² + x + 0,3.

b) Với x là khoảng cách từ người phát cầu đến lưới thì cầu phát được qua lưới khi và chỉ khi y ( x ) > 1,5 hay –0,17x² + x + 0,3 > 1,5 hay –0,17x² + x – 1,2 > 0.

Xét tam thức bậc hai f(x) = – 0,17x² + x – 1,2 có ∆ = 1² – 4.(– 0,17).(– 1,2) = 0,184 > 0 nên f(x) có hai nghiệm phân biệt x₁ ≈ 4,20 và x₂ ≈ 1,68.

Ta có a = – 0,17 < 0 suy ra f(x) > 0 khi 1,68 < x < 4,20.

Vậy người phát cầu cần đứng cách lưới trong khoảng từ 1,68 m đến 4,20 m.

Bài 10 trang 23 SBT Toán 10 Tập 2: Cho tam giác ABC và ABD cùng vuông tại A như Hình 3 có AB = x, BC = 5 và BD = 6.

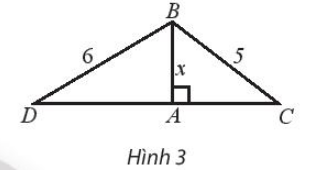
a) Biểu diễn độ dài cạnh AC và AD theo x.

b) Tìm x để chu vi của tam giác ABC là 12.

c) Tìm x để AD = 2AC

Lời giải:

a) Vì x là khoảng cách AB nên x > 0

Áp dụng định lí Phytagoras cho tam giác ABC:

AB² + AC² = BC²

⇒ AC² = 5² – x²

Như vậy AC = $\sqrt{25-{\text{x}}^{\text{2}}}$

Áp dụng định lí Phytagoras cho tam giác ABD:

AB² + AD² = BD²

⇒ AD² = 6² – x²

Như vậy AD = $\sqrt{36-{\text{x}}^{\text{2}}}$

b) Giải phương trình AB + AC + BC = 12

⇒ x + 5 + $\sqrt{25-{\text{x}}^{\text{2}}}$ = 12

⇒ $\sqrt{25-{\text{x}}^{\text{2}}}$ = 7 – x

⇒ 25 – x² = (7 – x)²

⇒ 2x² – 14x + 24 = 0

⇒ x = 4 hoặc x = 3

Thay lần lượt các giá trị trên vào phương trình AB + AC + BC = 12 ta thấy x = 4 và  x = 3 đều thoả mãn. Vậy x = 4 hoặc x = 3 để chu vi tam giác ABC là 12.

c) Ta có AD = 2AC

⇒ $\sqrt{36-{\text{x}}^{\text{2}}}$ = 2$\sqrt{25-{\text{x}}^{\text{2}}}$

⇒ 36 – x² = 100 – 4x²

⇒ 3x²  –  64 = 0

⇒ x = $\frac{8\sqrt{3}}{3}$ hoặc x = $-\frac{8\sqrt{3}}{3}$ mà x > 0 nên x = $\frac{8\sqrt{3}}{3}$.

Thay x = $\frac{8\sqrt{3}}{3}$ vào phương trình AD = 2AC thấy thỏa mãn. Vậy x = $\frac{8\sqrt{3}}{3}$.

Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Phương trình quy về phương trình bậc hai

Bài 1: Quy tắc cộng và quy tắc nhân

Bài 2: Hoán vị, chỉnh hợp và tổ hợp

Bài 3: Nhị thức Newton

Lý thuyết Chương 4: Bất phương tình bậc hai một ẩn

1. Tam thức bậc hai

– Đa thức bậc hai f(x) = ax² + bx + c với a, b, c là các hệ số, a ≠ 0 và x là biến số được gọi là tam thức bậc hai.

Cho tam thức bậc hai f(x) = ax² + bx + c (a ≠ 0). Khi thay x bằng giá trị x₀ vào f(x), ta được  gọi là giá trị của tam thức bậc hai  tại x₀.

• Nếu f(x₀) > 0 thì ta nói f(x) dương tại x₀.

• Nếu f(x₀) < 0 thì ta nói f(x) âm tại x₀.

• Nếu f(x) dương (âm) tại mọi điểm x thuộc một khoảng hoặc một đoạn thì ta nói f(x) dương (âm) trên khoảng hoặc đoạn đó.

Ví dụ: Biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy xét dấu của nó tại x = 3.

a) f(x) = x² + 2x⁴ – 2;

b) f(x) = –x² + 2x – 3;

c) f(x) = 3x² – $\sqrt{5}$x.

Hướng dẫn giải

a) Biểu thức f(x) = x² + 2x⁴ – 2 không phải là tam thức bậc hai vì có chứa x⁴.

b) Biểu thức f(x) = –x² + 2x – 3 là tam thức bậc hai với a = –1, b = 2 và c = –3.

Khi x = 3 ta có:

f(3) = –3² + 2.3 – 3 = = –9 + 6 – 3 = –6 < 0.

Do đó f(x) âm tại x = 3.

c) Biểu thức f(x) = 3x² – $\sqrt{5}$x là tam thức bậc hai với a = 3, b = $-\sqrt{5}$  và c = 0.

Khi x = 3 ta có:

f(3) = 3.3² – $\sqrt{5}$.3 = 27 – 3$\sqrt{5}$ > 0

Do đó f(x) dương tại x = 3.

– Cho tam thức bậc hai f(x) = ax² + bx + c (a ≠ 0). Khi đó:

• Nghiệm của phương trình bậc hai ax² + bx + c là nghiệm của f(x).

• Biểu thức ∆ = b² – 4ac và ${\Delta }^{\text{'}}={\left(\frac{b}{2}\right)}^2-ac$ lần lượt là biệt thức và biệt thức rút gọn của f(x).

Ví dụ: Tìm biệt thức (hoặc biệt thức thu gọn) và nghiệm (nếu có) của các tam thức bậc hai sau:

a) f(x) = x² + 2x – 5;

b) f(x) = = –3x² + 18x – 27;

c) f(x) = x + x² + 1.

Hướng dẫn giải

a) f(x) = x² + 2x – 5 có ∆' = 1² – 1.(–5) = 6 > 0.

Do đó f(x) có hai nghiệm phân biệt là:

$x_1=-1+\sqrt{6}$ và  $x_2=-1-\sqrt{6}$

Vậy tam thức bậc hai đã cho có hai nghiệm là $x_1=-1+\sqrt{6}$  và $x_2=-1-\sqrt{6}$  

b) f(x) = –3x² + 18x – 27

f(x) có ∆' = 9² – (‒3).(–27) = 0

Do đó f(x) có nghiệm kép là $x=\frac{-9}{-3}=3$  

Vậy tam thức bậc hai đã cho có nghiệm là x = 3.

c) f(x) = x + x² + 1 = x² + x + 1.

f(x) có ∆ = 1² – 4.1.1 = –3 < 0.

Do đó f(x) vô nghiệm.

Vậy tam thức bậc hai đã cho vô nghiệm.

2. Định lí về dấu của tam thức bậc hai

Cho tam thức bậc hai f(x) = ax² + bx + c (a ≠ 0).

+  Nếu ∆ < 0 thì f(x) cùng dấu với a với mọi giá trị x.

+ Nếu ∆ = 0 và $x_0=-\frac{b}{2a}$ là nghiệm kép của f(x) thì f(x) cùng dấu với a với mọi x khác x₀.

+ Nếu ∆ > 0 và x₁, x₂ là hai nghiệm của f(x) (x₁ < x₂) thì:

• f(x) trái dấu với a với mọi x trong khoảng (x₁; x₂);

• f(x) cùng dấu với a với mọi x thuộc hai khoảng (–∞; x₁), (x₂; +∞).

Chú ý:

+ Để xét dấu tam thức bậc hai f(x) = ax² + bx + c (a ≠ 0), ta thực hiện các bước sau:

Bước 1: Tính và xác định dấu của biệt thức ∆;

Bước 2: Xác định nghiệm của f(x) (nếu có);

Bước 3: Xác định dấu của hệ số a;

Bước 4: Xác định dấu của f(x).

+ Khi xét dấu của tam thức bậc hai, ta có thể dùng biệt thức thu gọn ∆' thay cho biệt thức ∆.

Ví dụ: Xét dấu của các tam thức bậc hai sau:

a) f(x) = 3x² + 6x – 9;

b) f(x) = –2x² + 8x + 10;

c) f(x) = 4x² + 8x + 4;

d) f(x) = –3x² + 2x – 1.

Hướng dẫn giải

a) f(x) = 3x² + 6x – 9

f(x) có a = 3 > 0 và ∆' = 3² – 3.(–9) = 36 > 0.

Khi đó f(x) có hai nghiệm phân biệt là:

$x_1=\frac{-3+\sqrt{36}}{3}=1$ và  $x_1=\frac{-3-\sqrt{36}}{3}=-3$

Ta có bảng xét dấu của f(x) như sau:

Vậy, f(x) dương trong khoảng (–∞; –3) và (1; +∞);

f(x) âm trong khoảng (–3; 1).

b) f(x) = –2x² + 8x + 10

f(x) có a = –2 < 0 và ∆' = 4² – (–2).10 = 36 > 0.

Khi đó f(x) có hai nghiệm phân biệt là:

$x_1=\frac{-4+\sqrt{36}}{-2}=-1$ và  $x_2=\frac{-4-\sqrt{36}}{-2}=5$

Ta có bảng xét dấu của f(x) như sau:

Vậy, f(x) âm trong khoảng (–∞; –1) và (5; +∞);

f(x) dương trong khoảng (–1; 5).

c) f(x) = 4x² + 8x + 4

f(x) có a = 4 > 0 và ∆' = 4² – 4.4 = 0.

Khi đó f(x) có nghiệm kép là $x=\frac{-4}{4}=-1$   

Vậy, f(x) dương với mọi x ≠ –1.

d) f(x) = –3x² + 2x – 1.

f(x) có a = –3 < 0 và ∆' = 1² – (–3).(–1) = –2 < 0.

Vậy f(x) âm với mọi x ∈ ℝ.

3. Giải bất phương trình bậc hai một ẩn

– Bất phương trình bậc hai một ẩn x là bất phương trình có một trong các dạng:

ax² + bx + c ≤ 0, ax² + bx + c < 0, ax² + bx + c ≥ 0, ax² + bx + c > 0, với a ≠ 0.

Nghiệm của bất phương trình bậc hai là các giá trị của biến x mà khi thay vào bất phương trình ta được bất đẳng thức đúng.

Ví dụ: Bất phương trình nào sau đây là bất phương trình bậc hai một ẩn? Nếu là bất phương trình bậc hai một ẩn, x = –2 và x = 3 có phải là nghiệm của bất phương trình đó hay không?

a) 2x² – 7x – 15 < 0;

b) 3 – 2x² + x³ > 0;

c) x² – 4x + 3 ≥ 0.

Hướng dẫn giải

a) 2x² – 7x – 15 < 0

Bất phương trình trên là bất phương trình bậc hai một ẩn dạng ax² + bx + c < 0 với a = 2, b = –7, c = –15.

• Với x = –2 thay vào bất phương trình ta có:

2.(–2)² – 7.(–2) – 15 < 0

$\Rightarrow$ 7 < 0. Đây là bất đẳng thức sai.

Do đó x = –2 không là nghiệm của bất phương trình.

• Với x = 3 thay vào bất phương trình ta có:

2.3² – 7.3 – 15 < 0

$\Rightarrow$ –18 < 0. Đây là bất đẳng thức đúng.

Do đó x = 3 là nghiệm của bất phương trình.

b) 3 – 2x² + x³ > 0

Bất phương trình trên không là bất phương trình bậc hai một ẩn vì có chứa x³.

c) x² – 4x + 3 ≥ 0.

Bất phương trình trên là bất phương trình bậc hai một ẩn dạng ax² + bx + c ≥ 0 với a = 1, b = –4, c = 3.

• Với x = –2 thay vào bất phương trình ta có:

(–2)² – 4.(–2) + 3 ≥ 0$\iff$ 15 ≥ 0. Đây là bất đẳng thức đúng.

Do đó x = –2 là nghiệm của bất phương trình.

• Với x = 3 thay vào bất phương trình ta có:

3² – 4.3 + 3 ≥ 0$\Rightarrow$ 0 ≥ 0. Đây là bất đẳng thức đúng.

Do đó x = 3 là nghiệm của bất phương trình.

– Giải bất phương trình bậc hai là tìm tập hợp các nghiệm của bất phương trình đó.

Ta có thể giải bất phương trình bậc hai bằng cách xét dấu của tam thức bậc hai tương ứng.

Ví dụ: Giải các bất phương trình sau:

a) x² – 3x + 2 < 0;

b) –2x² + 3x – 7 ≥ 0.

Hướng dẫn giải

a) x² – 3x + 2 < 0

Xét tam thức bậc hai f(x) = x² – 3x + 2

Ta có ∆ = (–3)² – 4.1.2 = 1 > 0

Do đó f(x) có hai nghiệm phân biệt là x₁ = 1 và x₂ = 2.

Vì a = 1 > 0 nên ta có bảng xét dấu của f(x) như sau:

Dựa vào bảng xét dấu f(x) < 0 $\iff$ x ∈ (1; 2).

Vậy bất phương trình đã cho có tập nghiệm là (1; 2).

b) –2x² + 3x – 7 ≥ 0.

Xét tam thức bậc hai f(x) = –2x² + 3x – 7

Ta có ∆ = 3² – 4.(–2).(–7) = –47 < 0.

Mặt khác a = –2 < 0

Do đó f(x) < 0 với mọi x.

Khi đó không có giá trị nào của x thỏa mãn f(x) ≥ 0.

Vậy bất phương trình đã cho vô nghiệm.

4. Phương trình dạng $\sqrt{a{x}^2+bx+c}=\sqrt{d{x}^2+\text{ex}+f}$

Để giải phương trình $\sqrt{a{x}^2+bx+c}=\sqrt{d{x}^2+\text{ex}+f}$  ta làm như sau:

Bước 1: Bình phương hai vế của phương trình để được phương trình:

ax² + bx + c = dx² + ex + f

Bước 2: Giải phương trình nhận được ở Bước 1.

Bước 3: Thử lại xem các giá trị x tìm được ở Bước 2 có thoả mãn phương trình đã cho hay không và kết luận nghiệm.

Ví dụ: Giải phương trình sau: $\sqrt{x^2+3x-2}=\sqrt{x+1}$

Hướng dẫn giải

 $\sqrt{x^2+3x-2}=\sqrt{x+1}$    (1)

Bình phương hai vế của phương trình (1) ta có:

x² + 3x – 2 = x + 1

$\Rightarrow$ x² + 2x – 3 = 0

x = 1 hoặc x = –3.

• Với x = 1 thay vào phương trình (1) ta được:

$\sqrt{1^2+3.1-2}=\sqrt{1+1}$$\iff \sqrt{2}=\sqrt{2}$ (đúng)

Do đó x = 1 là nghiệm của phương trình (1).

• Với x = –3 ta thấy x + 1 = –3 +1 = –2 < 0 nên không tồn tại $\sqrt{x+1}.$

Do đó x = –3 không là nghiệm của phương trình (1).

Vậy phương trình đã cho có nghiệm x = 1.

5. Phương trình dạng $\sqrt{a{x}^2+bx+c}=dx+e$

Để giải phương trình $\sqrt{a{x}^2+bx+c}=dx+e$ ta làm như sau:

Bước 1: Bình phương hai vế của phương trình để được phương trình: ax² + bx + c = dx +e

Bước 2: Giải phương trình nhận được ở Bước 1.

Bước 3: Thử lại xem các giá trị x tìm được ở Bước 2 có thoả mãn phương trình đã cho hay không và kết luận nghiệm.

Ví dụ: Giải phương trình sau: $\sqrt{4+2x-x^2}=x-2$  

Hướng dẫn giải

 $\sqrt{4+2x-x^2}=x-2$      (2)

Bình phương hai vế phương trình (2) ta có:

4 + 2x – x² = (x – 2)²

$\Rightarrow$ 4 + 2x – x² = x² – 4x + 4

$\Rightarrow$ 2x² – 6x = 0

$\Rightarrow$ 2x(x – 3) = 0

$\Rightarrow$ x = 0 hoặc x = 3

• Với x = 0 thay vào phương trình (2) ta được:

 $\sqrt{4+2.0-0^2}=0-2$$\iff$2 = –2 (vô lí)

Do đó x = 0 không là nghiệm của phương trình (2).

• Với x = 3 thay vào phương trình (2) ta được:

$\sqrt{4+2.3-3^2}=3-2$$\iff$1 = 1 (đúng)

Do đó x = 3 là nghiệm của phương trình (1).

Vậy phương trình đã cho có nghiệm x = 3.