Bất phương trình nào có tập nghiệm là (2; 5)

Bất phương trình nào có tập nghiệm là (2; 5)

Nguyễn Thị Thuỳ Linh Ngày: 22-11-2022 Lớp 10

1.1 K

Với giải Bài 6 trang 20 SBT Toán lớp 10 Chân trời sáng tạo chi tiết trong Bài tập cuối chương 7 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 10. Mời các bạn đón xem:

Giải sách bài tập Toán lớp 10 Bài tập cuối chương 7

Câu 6 trang 20 SBT Toán 10 Tập 2: Bất phương trình nào có tập nghiệm là (2; 5)?

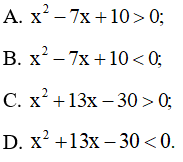
Sách bài tập Toán 10 Bài tập cuối chương 7 - Chân trời sáng tạo (ảnh 1)

Lời giải:

Đáp án đúng là B

+) Tam thức bậc hai f ( x ) = x² – 7x +10 có ∆ = ( – 7)² – 4.1.10 = 9 > 0 nên f(x) có hai nghiệm phân biệt x₁ = 2 và x₂ = 5, và a = 1 > 0 nên ta có:

f ( x ) > 0 với x < 2 hoặc x > 5.

f ( x ) < 0 với 2 < x < 5.

Do đó A sai, B đúng.

+) Tam thức bậc hai f ( x ) = $x^{2} + 13 x - 30$ có ∆ = 13² – 4.1.(– 30) = 289 > 0 nên f(x) hai nghiệm phân biệt x₁ = 2 và x₂ = –15, và a = 1 > 0 nên ta có:

f ( x ) > 0 với x < –15 hoặc x > 2.

f ( x ) < 0 với –15 < x < 2.

Do đó C, D sai.

Vậy đáp án đúng là B.

Xem thêm các bài giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Câu 1 trang 19 SBT Toán 10 Tập 2: Tam thức bậc hai nào có biệt thức ∆ = 1 và hai nghiệm là: $x_{1} = \frac{3}{2}$ và $x_{2} = \frac{7}{4} ?$ ...

Câu 2 trang 19 SBT Toán 10 Tập 2: Tam thức bậc hai nào dương với mọi $x \in ℝ$ ?...

Câu 3 trang 19 SBT Toán 10 Tập 2: Khẳng định nào sau đây đúng với tam thức bậc hai $f (x) = 10 x^{2} - 3 x - 4 ?$ ...

Câu 4 trang 19 SBT Toán 10 Tập 2: Trong trường hợp nào tam thức bậc hai f(x) = ax² + bx + c có $Δ > 0$ và a < 0?...

Câu 5 trang 20 SBT Toán 10 Tập 2: Cho đồ thị của hàm số bậc hai y = f(x) như Hình 1...

Câu 7 trang 20 SBT Toán 10 Tập 2: Tập xác định của hàm số $y = \frac{1}{\sqrt{9 x^{2} - 3 x - 2}} + \sqrt{3 - x}$ là:...

Câu 8 trang 20 SBT Toán 10 Tập 2: Với giá trị nào của tham số m thì phương trình $(2 m + 6) x^{2} + 4 m x + 3 = 0$ có hai nghiệm phân biệt?...

Câu 9 trang 20 SBT Toán 10 Tập 2: Giá trị nào là nghiệm của phương trình $\sqrt{x^{2} + x + 11} = \sqrt{- 2 x^{2} - 13 x + 16} ?$ ...

Câu 10 trang 20 SBT Toán 10 Tập 2: Khẳng định nào đúng với phương trình $\sqrt{2 x^{2} - 3 x - 1} = \sqrt{3 x^{2} - 2 x - 13} ?$ ...

Câu 11 trang 20 SBT Toán 10 Tập 2: Khẳng định nào đúng với phương trình $\sqrt{5 x^{2} + 27 x + 36} = 2 x + 5 ?$ ...

Câu 12 trang 20 SBT Toán 10 Tập 2: Cho đồ thị của hai hàm số bậc hai f(x) = ax² + bx + c và g(x) = dx² + ex + h như Hình 2...

Bài 1 trang 21 SBT Toán 10 Tập 2: Dựa vào đồ thị của hàm số bậc hai $y = f (x)$ sau đây, hãy xét dấu của tam thức bậc hai f(x)...

Bài 2 trang 21 SBT Toán 10 Tập 2: Xét dấu của các tam thức bậc hai sau:...

Bài 3 trang 21 SBT Toán 10 Tập 2: Giải các bất phương trình bậc hai sau:...

Bài 4 trang 22 SBT Toán 10 Tập 2: Dựa vào đồ thị của hàm số bậc hai được cho, hãy giải các bất phương trình sau:...

Bài 5 trang 22 SBT Toán 10 Tập 2: Giải các phương trình sau:...

Bài 6 trang 22 SBT Toán 10 Tập 2: Tìm tập xác định của các hàm số sau:...

Bài 7 trang 22 SBT Toán 10 Tập 2: Tìm các giá trị của tham số m để:...

Bài 8 trang 22 SBT Toán 10 Tập 2: Người ta thử nghiệm ném một quả bóng trên Mặt Trăng. Nếu quả bóng được ném lên từ độ cao h₀ (m) so với bề mặt của Mặt Trăng với vận tốc v₀ (m/s) thì độ cao của bóng sau t giây được cho bởi hàm số $h (t) = - \frac{1}{2} g t^{2} + v_{0} t + h_{0}$ với g = 1,625 m/s² là gia tốc trọng trường của Mặt Trăng...

Bài 9 trang 23 SBT Toán 10 Tập 2: Một người phát cầu qua lưới từ độ cao y₀ mét, nghiêng một góc so với phương ngang với vận tốc đầu v₀...

Bài 10 trang 23 SBT Toán 10 Tập 2: Cho tam giác ABC và ABD cùng vuông tại A như Hình 3 có AB = x, BC = 5 và BD = 6...

Xem thêm các bài giải SBT Toán 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Phương trình quy về phương trình bậc hai

Bài tập cuối chương 7

Bài 1: Quy tắc cộng và quy tắc nhân

Bài 2: Hoán vị, chỉnh hợp và tổ hợp

Bài 3: Nhị thức Newton

Từ khóa :

toán 10 Giải sách bài tập Bài tập cuối chương 7

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Chứng minh rằng biểu thức sau luôn luôn dương với mọi x, y: B = x^2 - 2x + y^2 + 4y + 6

Chứng minh rằng biểu thức sau luôn luôn dương với mọi x, y: B = x^2 - 2x + y^2 + 4y + 6 Lữ Ngọc My My

55

Toán Tổng hợp kiến thức

3/(1^2.2^2 ) + 5/(2^2.3^2 ) + 7/(3^2.4^2 ) + ... + 19/(9^2.10^2). Chứng minh nhỏ hơn 1

3/(1^2.2^2 ) + 5/(2^2.3^2 ) + 7/(3^2.4^2 ) + ... + 19/(9^2.10^2). Chứng minh nhỏ hơn 1 Lữ Ngọc My My

52

Toán Tổng hợp kiến thức

Tính tổng: 1/4 + 1/12 + 1/24 + 1/40 + 1/60 + 1/84

Tính tổng: 1/4 + 1/12 + 1/24 + 1/40 + 1/60 + 1/84 Lữ Ngọc My My

42

Toán Tổng hợp kiến thức

Tìm x; y nguyên 2xy + 2x - y = 8

Tìm x; y nguyên 2xy + 2x - y = 8 Lữ Ngọc My My

43

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.