Với giải sách bài tập Toán 7 Bài 1: Góc ở vị trí đặc biệt sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 7. Mời các bạn đón xem:

Giải SBT Toán lớp 7 Bài 1: Góc ở vị trí đặc biệt

Giải Toán 7 trang 103 Tập 1

Bài 1 trang 103 Toán 7 Tập 1:

Quan sát Hình 8 và chỉ ra:

a) Bốn cặp góc kề nhau;

b) Ba cặp góc kề bù (khác góc bẹt);

c) Hai cặp góc đối đỉnh (khác góc bẹt và góc không)

Lời giải:

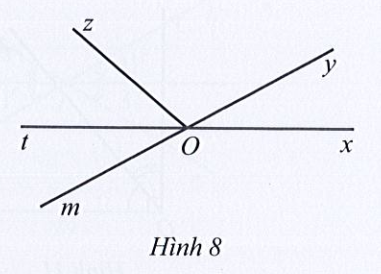
Quan sát Hình 8 ta thấy:

a) Bốn cặp góc kề nhau như: $\widehat{mOt}$ và $\widehat{tOz}$, $\widehat{mOt}$ và $\widehat{tOy}$, $\widehat{tOz}$ và $\widehat{zOy}$, $\widehat{zOy}$ và $\widehat{yOx}$

b) Ba cặp góc kề bù (khác góc bẹt) như: $\widehat{mOt}$ và $\widehat{tOy};$ $\widehat{tOz}$ và $\widehat{zOx}$. $\widehat{mOz}$ và $\widehat{zOy}$

c) Hai cặp góc đối đỉnh (khác góc bẹt và góc không) là: $\widehat{mOt}$ và $\widehat{yOx};$ $\widehat{tOy}$ và $\widehat{xOm}.$

Bài 2 trang 103 Toán 7 Tập 1: Cho các cặp tia Oa và Ob, Oc và Od là các cặp tia đối nhau. Tìm số đo mỗi góc aOc, bOc, bOd, aOd trong mỗi trường hợp sau:

a) $\widehat{aOc}=75º;$

b) $\widehat{aOc}+\widehat{bOd}=140°;$

c) $\widehat{aOc}+\widehat{bOd}=\widehat{bOc}+\widehat{aOd };$

d) $\widehat{bOc}-\widehat{aOc}=10°;$

e) $\widehat{bOc}=2\widehat{aOc}.$

Lời giải:

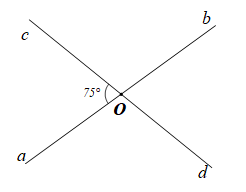
Vì các cặp tia Oa và Ob, Oc và Od là các cặp tia đối nhau nên ta có:

• $\widehat{aOc}$ và $\widehat{bOd}$ là hai góc đối đỉnh nên $\widehat{aOc}=\widehat{bOd};$

• $\widehat{aOc}$ và $\widehat{bOc}$ là hai góc kề bù nên $\widehat{aOc}+\widehat{bOc}=180°;$

• $\widehat{bOc}$ và $\widehat{aOd}$ là hai góc đối đỉnh nên $\widehat{aOd}=\widehat{bOc}.$

a) $\widehat{aOc}=75º$

Vì $\widehat{aOc}=\widehat{bOd}$ (hai góc đối đỉnh) mà $\widehat{aOc}=75º$ nên $\widehat{bOd}=\widehat{aOc}=75°.$

Vì $\widehat{aOc}+\widehat{bOc}=180°$ (hai góc kề bù)

Suy ra

$$\begin{gathered} \widehat{bOc}=180°-\widehat{aOc} \\ =180°-75°=105°. \end{gathered}$$

Do đó $\widehat{aOd}=\widehat{bOc}=105°.$

Vậy $\widehat{bOd}=\widehat{aOc}=75°$ và $\widehat{aOd}=\widehat{bOc}=105°.$

b) • Vì $\widehat{aOc}=\widehat{bOd}$ (hai góc đối đỉnh)

Mà $\widehat{aOc}+\widehat{bOd}=140°$ 

Nên $\widehat{aOc}+\widehat{aOc}=140°$ hay $2\widehat{aOc}=140°$

Suy ra $\widehat{aOc}=\frac{140°}{2}=70°$

Do đó $\widehat{aOc}=\widehat{bOd}=70°$

• Vì $\widehat{aOc}+\widehat{bOc}=180°$ (hai góc kề bù)

Suy ra $\widehat{bOc}=180°-\widehat{aOc}=180°-70°=110°.$

Do đó $\widehat{aOd}=\widehat{bOc}=110°.$

Vậy $\widehat{bOd}=\widehat{aOc}=70°$ và $\widehat{aOd}=\widehat{bOc}=110°.$

c) Vì $\widehat{aOc}=\widehat{bOd};$ $\widehat{aOd}=\widehat{bOc};$ nên ta có:

$\widehat{aOc}+\widehat{aOc}=\widehat{bOc}+\widehat{bOc}$ hay $2\widehat{aOc}=2\widehat{bOc}$

Do đó $\widehat{aOc}=\widehat{bOc}$ 

Mà $\widehat{aOc}+\widehat{bOc}=180°$ nên $\widehat{aOc}+\widehat{aOc}=180°$

Hay $2\widehat{aOc}=180°$ do đó $\widehat{aOc}=\frac{180°}{2}=90°.$

Vậy $\widehat{aOc}=\widehat{bOd}=\widehat{aOd}=\widehat{bOc}=90°.$

d) Vì $\widehat{bOc}-\widehat{aOc}=10°$ nên $\widehat{bOc}=\widehat{aOc}+10°$

Mà $\widehat{aOc}+\widehat{bOc}=180°$ 

Do đó $\widehat{aOc}+\widehat{aOc}+10°=180°$

Hay $2\widehat{aOc}+10°=180°$

Suy ra $2\widehat{aOc}=180°-10°=170°$

Do đó $\widehat{aOc}=\frac{170°}{2}=85°$

Khi đó

$$\begin{gathered} \widehat{bOc}=\widehat{aOc}+10° \\ =85°+10°=95° \end{gathered}$$

Suy ra $\widehat{bOd}=\widehat{aOc}=85°$ và $\widehat{bOc}=\widehat{aOd}=95°.$

Vậy $\widehat{bOd}=\widehat{aOc}=85°$ và $\widehat{bOc}=\widehat{aOd}=95°.$

e) Vì $\widehat{bOc}=2\widehat{aOc}$ và $\widehat{aOc}+\widehat{bOc}=180°$ nên ta có:

$\widehat{aOc}+2\widehat{aOc}=180°$ hay $3\widehat{aOc}=180°$

Suy ra $\widehat{aOc}=\frac{180°}{3}=60°$

Khi đó $\widehat{bOc}=2\widehat{aOc}=2.60°=120°.$

Suy ra $\widehat{bOd}=\widehat{aOc}=60°$ và $\widehat{bOc}=\widehat{aOd}=120°.$

Vậy $\widehat{bOd}=\widehat{aOc}=60°$ và $\widehat{bOc}=\widehat{aOd}=120°.$

Giải Toán 7 trang 104 Tập 1

Bài 3 trang 104 Toán 7 Tập 1: Quan sát Hình 9.

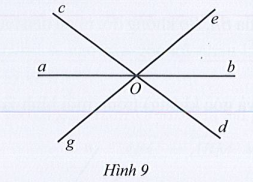
a) Hai góc aOg và cOe có phải là hai góc đối đỉnh hay không? Vì sao?

b) Tìm các cặp góc đối đỉnh (khác góc bẹt và góc không) ở Hình 9.

c) Chứng tỏ rằng $\widehat{aOg}+\widehat{cOe}+\widehat{bOd}=180°.$

Lời giải:

a) Hai góc aOg và cOe không phải là hai góc đối đỉnh vì tia Og và Oe là hai tia đối nhưng tia Oa và Oc không là hai tia đối.

b) Trong Hình 9 có các cặp góc đối đỉnh là: $\widehat{aOc}$ và $\widehat{bOd},$ $\widehat{aOe}$ và $\widehat{bOg},$ $\widehat{cOe}$ và $\widehat{dOg},$ $\widehat{cOb}$ và $\widehat{dOa},$ $\widehat{eOb}$ và $\widehat{gOa},$ $\widehat{eOd}$ và $\widehat{gOc}.$ 

c) Ta có $\widehat{aOc}$ và $\widehat{bOd}$ là hai góc đối đỉnh nên $\widehat{aOc}=\widehat{bOd}$

Khi đó $\widehat{aOg}+\widehat{cOe}+\widehat{bOd}=$$\widehat{gOa}+\widehat{cOe}+\widehat{aOc}$

$$\begin{gathered} =\left(\widehat{gOa}+\widehat{aOc}\right)+\widehat{cOe} \\ =\widehat{gOc}+\widehat{cOe}=\widehat{gOe}=180° \end{gathered}$$

Vậy $\widehat{aOg}+\widehat{cOe}+\widehat{bOd}=180°.$

Bài 4 trang 104 Toán 7 Tập 1:

Quan sát Hình 10 và chỉ ra:

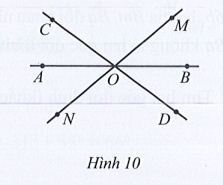
a) Bốn góc kề với góc AOC (không kể góc bẹt);

b) Hai góc kề bù với góc AOC.

Lời giải:

a) Bốn góc kề với $\widehat{AOC}$ (không kể góc bẹt) là: $\widehat{COM},\widehat{COB},\widehat{AON},\widehat{AOD}.$

b) Hai góc kề bù với $\widehat{AOC}$ là: $\widehat{COB},\widehat{AOD}.$

Bài 5 trang 104 Toán 7 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) Hai góc đối đỉnh thì bằng nhau.

b) Hai góc bằng nhau thì đối đỉnh.

c) Hai góc không đối đỉnh thì không bằng nhau.

Lời giải:

a) Hai góc đối đỉnh thì bằng nhau là phát biểu đúng.

b) Hai góc bằng nhau thì đối đỉnh là phát biểu sai.

Chẳng hạn, hai góc xOy và yOz bằng nhau (hình vẽ) nhưng không phải là hai góc đối đỉnh.

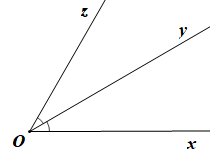
c) Hai góc không đối đỉnh thì không bằng nhau là phát biểu sai.

Chẳng hạn, hai góc xOy và yOz không đối đỉnh (hình vẽ) nhưng vẫn bằng nhau.

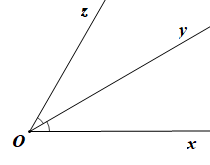
Bài 6 trang 104 Toán 7 Tập 1: Quan sát Hình 11.

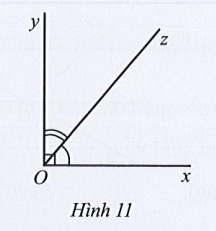
Tính số đo mỗi góc xOz, yOz biết $\frac{1}{5}\widehat{xOz}=\frac{1}{4}\widehat{yOz}.$

Lời giải:

Vì $\frac{1}{5}\widehat{xOz}=\frac{1}{4}\widehat{yOz}$ nên $\widehat{xOz}=\frac{5}{4}\widehat{yOz}.$

Do $\widehat{xOz}$ và $\widehat{zOy}$ là hai góc kề nhau nên:

$\widehat{xOz}+\widehat{zOy}=\widehat{xOy}$

Hay $\frac{5}{4}\widehat{yOz}+\widehat{yOz}=90°$

Do đó $\frac{9}{4}\widehat{yOz}=90°$

Suy ra $\widehat{yOz}=40°$

Khi đó $\widehat{xOz}=\frac{5}{4}\widehat{yOz}=\frac{5}{4}.40°=50°$

Vậy $\widehat{xOz}=50°.$ và $\widehat{yOz}=40°.$

Bài 7 trang 104 Toán 7 Tập 1: Quan sát Hình 12.

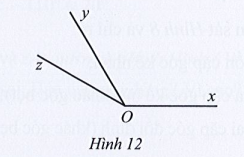
Cho hai góc xOy, yOz là hai góc kề nhau, $\widehat{xOz}=150°$ và $\widehat{xOy}-\widehat{yOz}=90°.$

a) Tính số đo mỗi góc xOy, yOz.

b) Vẽ các tia Ox' và Oy' lần lượt là tia đối của các tia Ox, Oy. Tính số đo mỗi góc x'Oy', y'Oz, xOy'.

Lời giải:

a) Vì $\widehat{xOy}-\widehat{yOz}=90°$ nên $\widehat{xOy}=\widehat{yOz}+90°$

Vì hai góc xOy, yOz là hai góc kề nhau nên:

$\widehat{xOy}+\widehat{yOz}=\widehat{xOz}$

Suy ra $\widehat{yOz}+90°+\widehat{yOz}=150°$

Hay $2\widehat{yOz}=150°-90°=60°$

Do đó $\widehat{yOz}=\frac{60°}{2}=30°$

Khi đó $\widehat{xOy}=\widehat{yOz}+90°=30°+90°=120°.$

Vậy $\widehat{xOy}=120°$ và $\widehat{yOz}=30°.$

b)

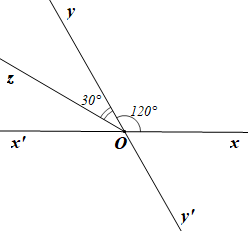
• Vì các tia Ox' và Oy' lần lượt là tia đối của các tia Ox, Oy nên $\widehat{x^{\text{'}}O{y}^{\text{'}}}$ và $\widehat{xOy}$ là hai góc đối đỉnh.

Do đó $\widehat{x^{\text{'}}O{y}^{\text{'}}}=\widehat{xOy}=120°.$

• Vì $\widehat{y^{\text{'}}Oz}$ và $\widehat{yOz}$ là hai góc kề bù nên ta có:

$\widehat{y^{\text{'}}Oz}+\widehat{zOy}=180°$

Suy ra $\widehat{y^{\text{'}}Oz}=180°-\widehat{yOz}$

Do đó $\widehat{y^{\text{'}}Oz}=180°-30°=150°.$

• Vì $\widehat{xO{y}^{\text{'}}}$ và $\widehat{xOy}$ là hai góc kề bù nên ta có:

$\widehat{xO{y}^{\text{'}}}+\widehat{xOy}=180°$

Suy ra $\widehat{xO{y}^{\text{'}}}=180°-\widehat{xOy}$

Do đó $\widehat{xO{y}^{\text{'}}}=180°-120°=60°.$

Vậy $\widehat{x^{\text{'}}O{y}^{\text{'}}}=120°,$ $\widehat{y^{\text{'}}Oz}=150°$ và $\widehat{xO{y}^{\text{'}}}=60°.$

Xem thêm các bài giải SBT Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài ôn tập chương 3

Bài 1 : Góc ở vị trí đặc biệt

Bài 2 : Tia phân giác của một góc

Bài 3 : Hai đường thẳng song song

Bài 4 : Định lí

Lý thuyết Góc ở vị trí đặc biệt

1. Hai góc kề nhau

Hai góc kề nhau là hai góc có đỉnh chung, có một cạnh chung và hai cạnh còn lại nằm về hai phía của đường thẳng chứa cạnh chung đó.

Ví dụ:

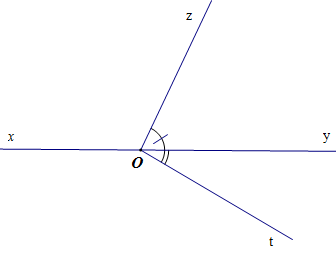Hai góc yOz và yOt trong hình vẽ có chung đỉnh O, có một cạnh chung là Oy, hai cạnh còn lại là Oz và Ot nằm về hai phía của đường thẳng xy.

Vì vậy hai góc yOz và yOt là hai góc kề nhau.

Tính chất:

- Cho góc xOz (khác góc bẹt) và tia Oy nằm trong góc đó. Khi đó hai góc xOy và yOz là hai góc kề nhau và $\widehat{xOz}=\widehat{xOy}+\widehat{yOz}$.

- Nếu góc xOz là góc bẹt thì với mỗi tia Oy (khác hai tia Ox, Oz), ta cũng có: $\widehat{xOz}=\widehat{xOy}+\widehat{yOz}$.

Ví dụ: Trong hình hai góc xOy và yOz có phải là hai góc kề nhau không? Tính số đo góc xOz ?

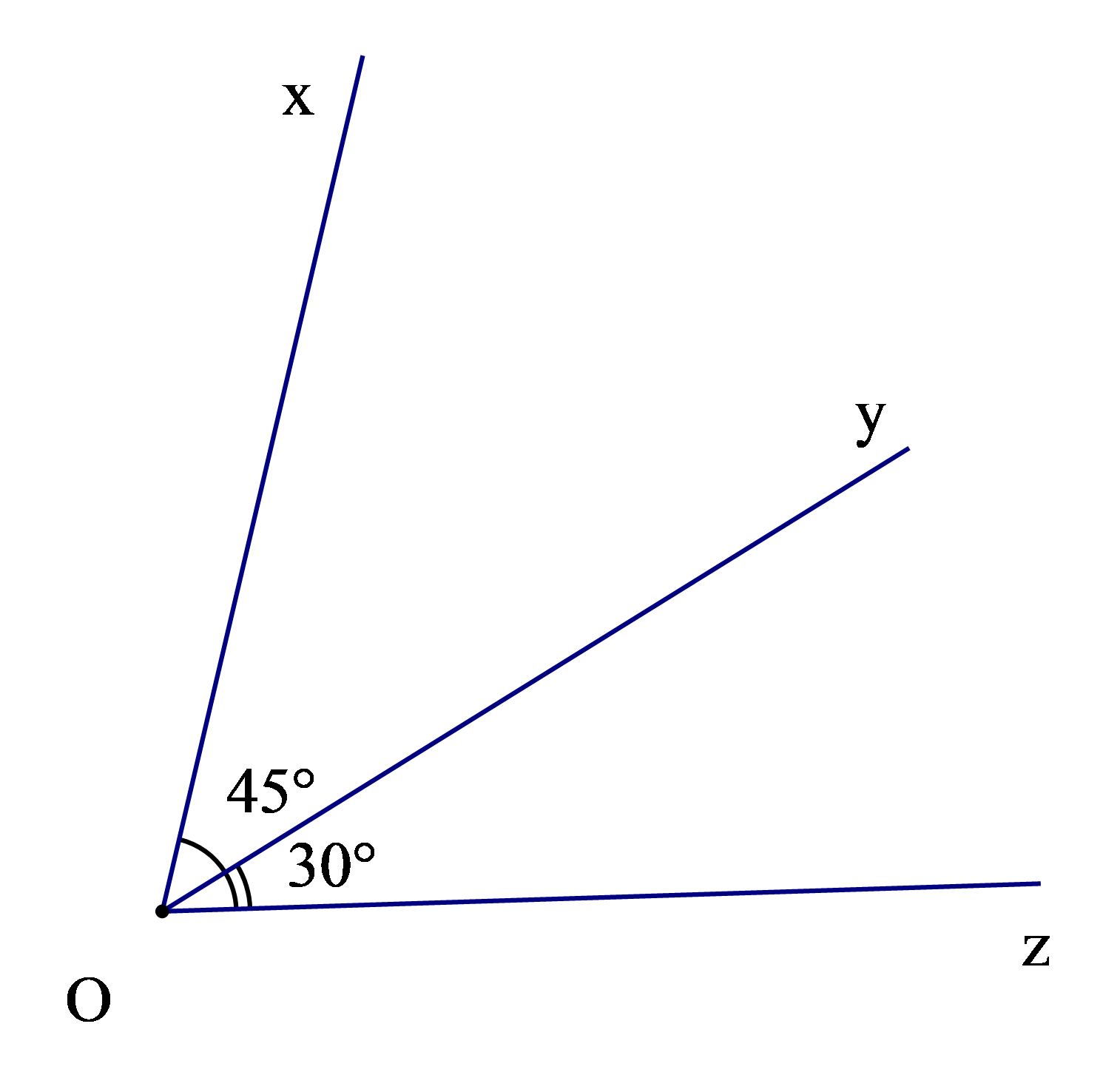Hướng dẫn giải

Tia Oy nằm trong góc xOz nên góc xOy và góc yOz là hai góc kề nhau.

Và $\widehat{xOz}=\widehat{xOy}+\widehat{yOz}=45°+30°=75°$.

Vậy hai góc xOy và yOz là hai góc kề nhau và $\widehat{xOz}=75°$.

2. Hai góc bù nhau. Hai góc kề bù

- Hai góc bù nhau là hai góc có tổng bằng 180°.

- Hai góc vừa kề nhau, vừa bù nhau gọi là hai góc kề bù.

Chú ý: Hai góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau là hai góc kề bù.

Ví dụ:

a)

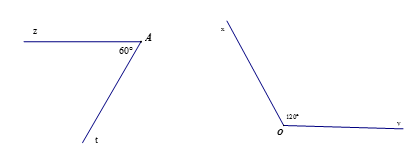
Ta có : $\widehat{zAt}+\widehat{xOy}=60°+120°=180°$.

Vì hai góc zAt và xOy có tổng bằng 180° nên góc zAt và xOy là hai góc bù nhau.

b)

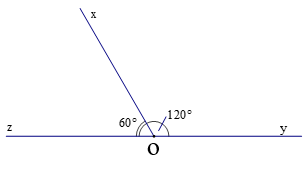- Hai góc xOz và góc xOy có đỉnh O chung và cạnh Ox chung ; Hai cạnh Oy và Oz nằm về hai phía của đường thẳng chứa tia Ox. Vì thế, hai góc xOz và góc xOy kề nhau.

- Ta có : $\widehat{xOz}+\widehat{xOy}=60°+120°=180°$, vậy nên hai góc xOz và xOy là hai góc bù nhau.

Hai góc xOz và xOy là hai góc vừa kề nhau vừa bù nhau.

Vậy, góc xOz và góc xOy là hai góc kề bù.

3. Hai góc đối đỉnh

- Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

- Hai góc đối đỉnh thì bằng nhau.

Ví dụ :

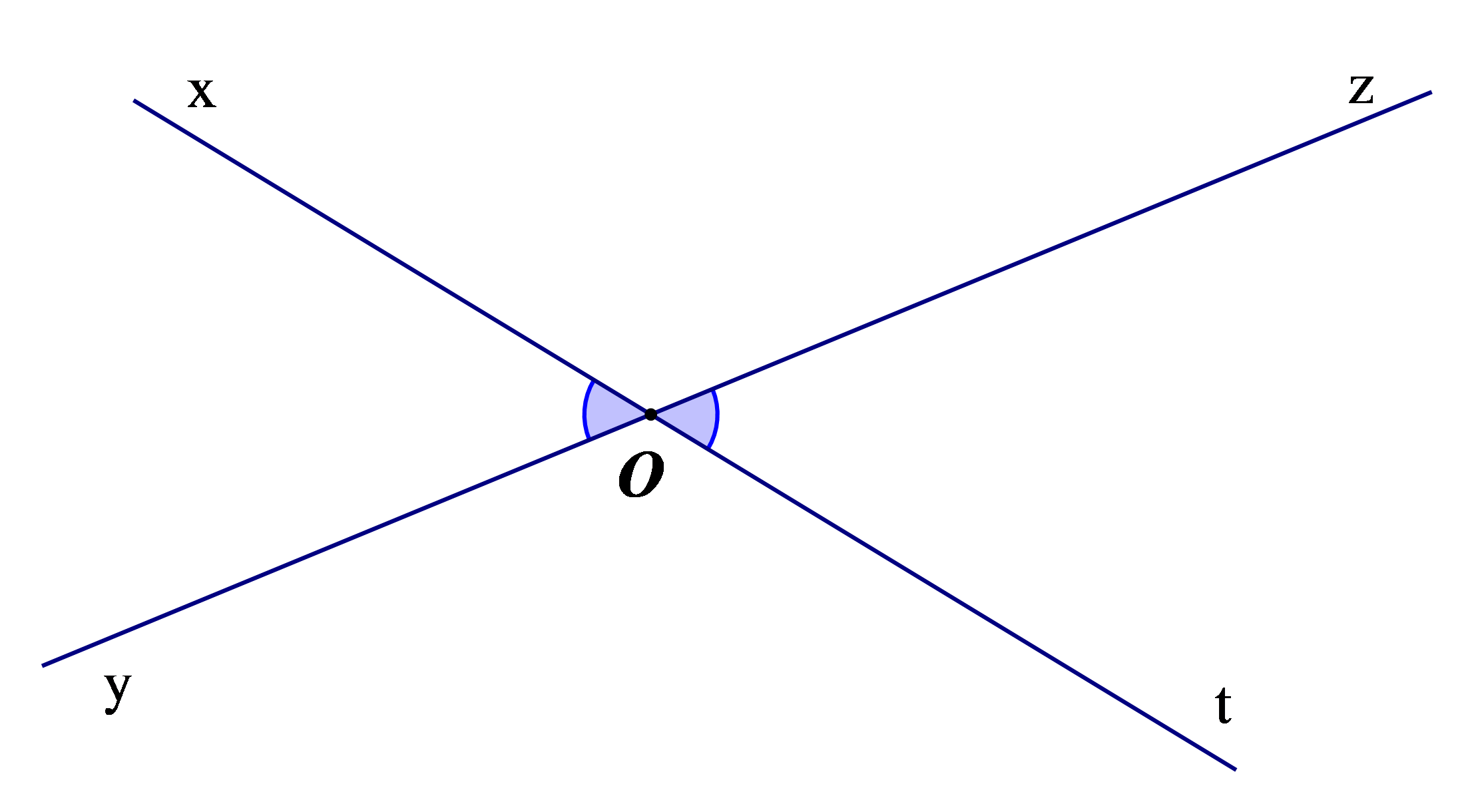Cạnh Ot của góc tOz là tia đối của cạnh Ox của góc xOy;

Cạnh Oz của góc tOz là tia đối của cạnh Oy của góc xOy;

Vì vậy, góc xOy và góc tOz là hai góc đối đỉnh, nên $\widehat{xOy}=\widehat{tOz}$.

Tương tự, góc xOz và góc tOy cũng là hai góc đối đỉnh, nên $\widehat{xOz}=\widehat{tOy}$.