Tailieumoi.vn xin giới thiệu Giải bài tập Toán 9 Bài 3: Góc nội tiếp hay, chi tiết giúp học sinh dễ dàng làm bài tập Góc nội tiếp lớp 9.

Giải bài tập Toán lớp 9 Bài 3: Góc nội tiếp

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 73 SGK Toán lớp 9 Tập 2:Vì sao các góc ở hình 14 và hình 15 không phải là góc nội tiếp ?

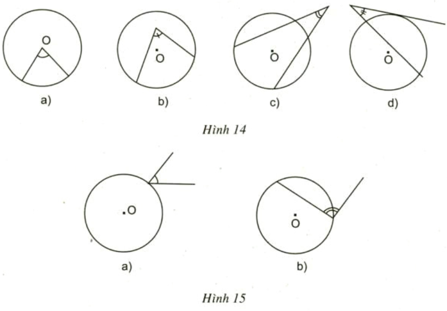
Lời giải:

- Các góc trên hình 14 không phải góc nội tiếp vì các góc này không có đỉnh nằm trên đường tròn.

- Các góc trên hình 15 không phải góc nội tiếp vì các góc này không có hai cạnh chứa hai dây cung của đường tròn.

Câu hỏi 2 trang 73 SGK Toán lớp 9 Tập 2: Bằng dụng cụ, hãy so sánh số đo của góc nội tiếp BAC với số đo của cung bị chắn BC trong mỗi hình 16, 17, 18 dưới đây.

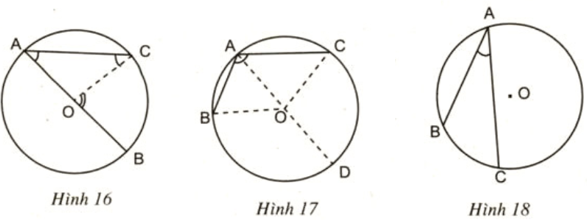
Lời giải:

Hình 16:

Dùng thước đo góc ta đo được:

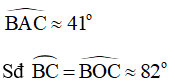
Hình 17:

Dùng thước đo góc ta đo được:

$\widehat{BAC}\approx {115}^o$

Sđ $\stackrel{⏜}{BDC}={360}^o-\widehat{BOC}$ $\approx {360}^o-{130}^o\approx {230}^o$

Hình 18:

Dùng thước đo góc ta đo được:

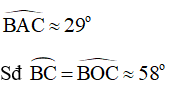
Từ các kết quả đo trên, ta có thể kết luận: Số đo của góc nội tiếp BAC bằng một nửa số đo của cung bị chắn BC.

Câu hỏi 3 trang 75 SGK Toán lớp 9 Tập 2: Hãy vẽ hình minh họa các tính chất:

a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau.

b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

c) Góc nội tiếp (nhỏ hơn hoặc bằng ${90}^0$) có số đo của góc ở tâm cùng chắn một cung.

d) Góc nội tiếp chắn nửa đường tròn là góc vuông.

Lời giải:

a)

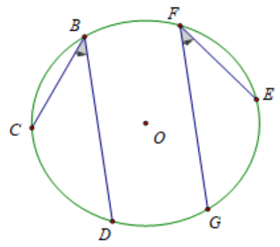
b)

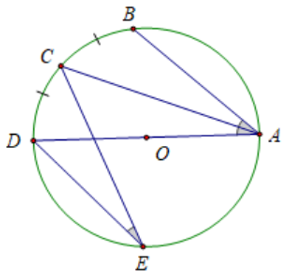
c)

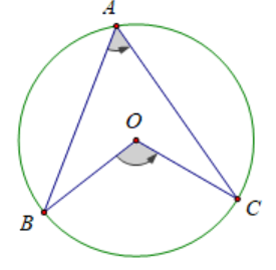
d)

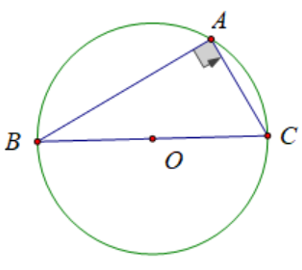
Bài tập (trang 75)

Bài tập 15 trang 75 SGK Toán lớp 9 Tập 2:Các khẳng định sau đây đúng hay sai?

a) Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.

b) Trong một đường tròn, các góc nội tiếp bằng nhau thì cùng chắn một cung.

Lời giải:

a) Đúng theo hệ quả: Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.

b) Sai vì trong một đường tròn, các góc nội tiết bằng nhau không nhất thiết cùng chắn một cung mà có thể chắn hai cung bằng nhau.

Bài tập 16 trang 75 SGK Toán lớp 9 Tập 2:Xem hình 19 (hai đường tròn có tâm là B, C và điểm B nằm trên đường tròn tâm C).

a) Biết $\widehat{MAN}={30}^o$, tính $\widehat{PCQ}$.

b) Nếu $\widehat{PCQ}={136}^o$ thì $\widehat{MAN}$ có số đo là bao nhiêu ?

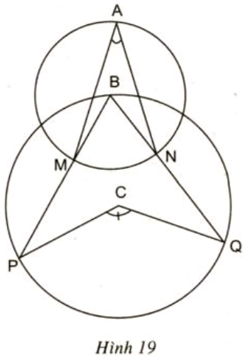
Lời giải:

a) Trong đường tròn (b), có góc MAN là góc nội tiếp chắn cung nhỏ MN và góc MBN là góc ở tâm chắn cung nhỏ MN nên ta có:

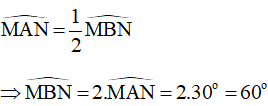
Trong đường tròn (C) , góc MBN là góc nội tiếp chắn cung nhỏ PQ và góc PCQ là góc ở tâm chắn cung nhỏ PQ nên ta có:

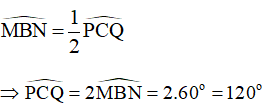
b) Trong đường tròn (C), góc MBN là góc nội tiếp chắn cung nhỏ PQ và góc PCQ là góc ở tâm chắn cung nhỏ PQ nên ta có:

$\widehat{MBN}=\frac{1}{2}\widehat{PCQ}$$=\frac{1}{2}{.136}^o={68}^o$

Trong đường tròn (b), có góc MAN là góc nội tiếp chắn cung nhỏ MN và góc MBN là góc ở tâm chắn cung nhỏ MN nên ta có:

$\widehat{MAN}=\frac{1}{2}\widehat{MBN}$$=\frac{1}{2}{.68}^o={34}^o$

Bài tập 17 trang 75 SGK Toán lớp 9 Tập 2: Muốn xác định tâm của một đường tròn mà chỉ dùng êke thì phải làm như thế nào ?

Lời giải:

Cách xác định:

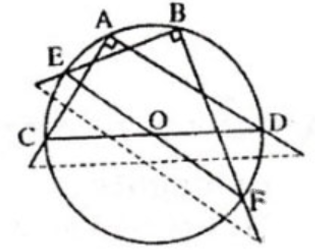
- Lấy 2 điểm A, B bất kỳ trên đường tròn.

- Đặt đỉnh của eke trùng với điểm A trên đường tròn. Vẽ hai đường thẳng là hai cạnh góc vuông của eke, lần lượt cắt đường tròn tại E, F. Nối EF.

- Đặt đỉnh của eke trùng với điểm B trên đường tròn. Vẽ hai đường thẳng là hai cạnh góc vuông của eke, lần lượt cắt đường tròn tại C, D. Nối CD.

 - EF cắt CD tại đâu đó chính là tâm đường tròn.

Bài tập 18 trang 75 SGK Toán lớp 9 Tập 2: Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn PQ. Bóng được đặt ở các vị trí A, B, C trên một cung tròn như hình 20. Hãy so sánh các góc $\widehat{PAQ}, \widehat{PBQ}, \widehat{PCQ}$.

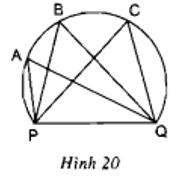
Lời giải:

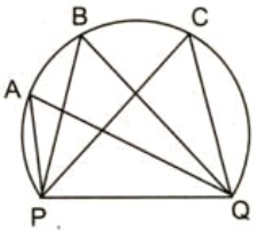
Với các vị trí A, B, C trên một cung tròn thì ta được các góc nội tiếp $\widehat{PAQ}, \widehat{PBQ}, \widehat{PCQ}$ cùng chắn cung nhỏ PQ, nên suy ra:

$\widehat{PAQ}=\widehat{PBQ}=\widehat{PCQ}$ (do trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau)

Vậy với các vị trí trên thì các góc sút đều bằng nhau, không có góc sút nào rộng hơn.

Luyện tập trang 75, 76

Bài tập 19 trang 75 SGK Toán lớp 9 tập 2: Cho đường tròn tâm O, đường kính AB và S là một điểm nằm bên ngoài đường tròn. SA và SB lần lượt cắt đường tròn tại M, N. Gọi H là giao điểm của BM và AN. Chứng minh rằng SH vuông góc với AB.

Lời giải:

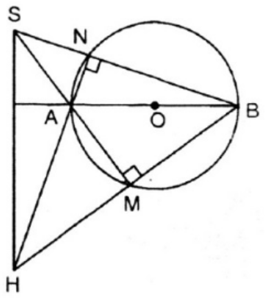
Trong đường tròn (O), $\widehat{\mathrm{AMB}}$ là góc nội tiếp chắn nửa đường tròn (O) nên ta có:

$\widehat{\mathrm{AMB}}={90}^{\mathrm{o}}$

$\Rightarrow \mathrm{BM}\perp \mathrm{AM}$ tại M

$\Rightarrow \mathrm{BM}\perp \mathrm{SA}$ tại M

Trong đường tròn (O), $\widehat{\mathrm{ANB}}$ là góc nội tiếp chắn nửa đường tròn (O) nên ta có: $\widehat{\mathrm{ANB}}={90}^{\mathrm{o}}$

$\Rightarrow \mathrm{AN}\perp \mathrm{BN}$ tại N

$\Rightarrow \mathrm{AN}\perp \mathrm{SB}$ tại N

Xét tam giác SAB có:

$\mathrm{BM}\perp \mathrm{SA}$ tại M

$\mathrm{HA}\perp \mathrm{BN}$ tại N

Do đó, BM và AN là hai đường cao của tam giác SAB

Mà BM cắt AN tại H

Do đó, H là trực tâm của tam giác SAB

$\Rightarrow \mathrm{SH}\perp \mathrm{AB}$ (đcpcm).

Bài tập 20 trang 76 SGK Toán lớp 9 tập 2: Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Vẽ các đường kính AC và AD của hai đường tròn. Chứng minh rằng ba điểm C, B, D thẳng hàng.

Lời giải:

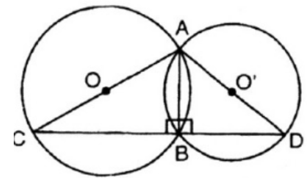
Xét đường tròn (O)

Có AC là đường kính nên $\widehat{\mathrm{ABC}}$ là góc nội tiếp chắn nửa đường tròn

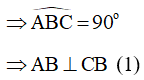
Xét đường tròn (O’) vì AD là đường kính nên $\widehat{\mathrm{ABD}}$ là góc nội tiếp chắn nửa đường tròn

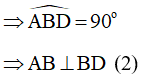
Từ (1), (2) ta suy ra: B, C, D thẳng hàng.

Bài tập 21 trang 76 SGK Toán lớp 9 tập 2: Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại A và B. Vẽ đường thẳng qua A cắt (O) tại M và cắt (O') tại N (A nằm giữa M và N). Hỏi MBN là tam giác gì ? Tại sao ?

Lời giải:

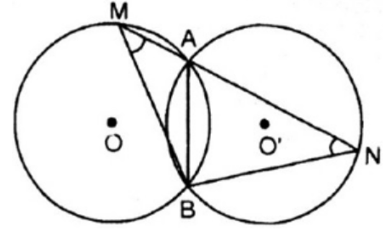
Hai đường tròn (O) và (O') bằng nhau cắt nhau tại hai điểm A và B nên cung nhỏ AB thuộc đường tròn (O) bằng cung nhỏ AB thuộc đường tròn (O’)

Mà ta có:

Trong đường tròn (O), góc AMB là góc nội tiếp chắn cung nhỏ AB

Trong đường tròn (O’), góc ANB là góc nội tiếp chắn cung nhỏ AB

$\Rightarrow \widehat{\mathrm{AMB}}=\widehat{\mathrm{ANB}}$

Xét tam giác BMN có:

$\widehat{\mathrm{AMB}}=\widehat{\mathrm{ANB}}$

Do đó, tam giác BMN cân tại B.

Bài tập 22 trang 76 SGK Toán lớp 9 tập 2: Trên đường tròn (O) đường kính AB, lấy điểm M (khác A và B). Vẽ tiếp tuyến của (O) tại A. Đường thẳng BM cắt tiếp tuyến đó tại C. Chứng minh rằng ta luôn có: ${\mathrm{MA}}^2=\mathrm{MB}.\mathrm{MC}$.

Lời giải

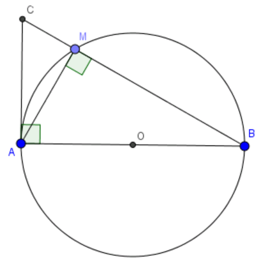
Xét đường tròn (O)

Góc AMB là góc nội tiếp chắn nửa đường tròn $\Rightarrow \widehat{\mathrm{AMB}}={90}^{\mathrm{o}}$

CA là tiếp tuyến của (O) tại A (gt)

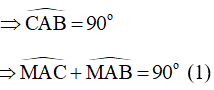
Xét tam giác AMB vuông tại M có:

$\widehat{\mathrm{MAB}}+\widehat{\mathrm{MBA}}={90}^{\mathrm{o}}$  (2)

Xét tam giác CAB vuông tại A có:

$\widehat{\mathrm{MCA}}+\widehat{\mathrm{MBA}}={90}^{\mathrm{o}}$ (3)

Từ (1) và (2) ta suy ra $\widehat{\mathrm{MBA}}=\widehat{\mathrm{MAC}}$ (cùng phụ $\widehat{\mathrm{MAB}}$)

Từ (2) và (3) ta suy ra $\widehat{\mathrm{MAB}}=\widehat{\mathrm{MCA}}$ (cùng phụ $\widehat{\mathrm{MBA}}$)

Xét tam giác MAB và tam giác MCA có:

$\widehat{\mathrm{MBA}}=\widehat{\mathrm{MAC}}$ (chứng minh trên)

$\widehat{\mathrm{MAB}}=\widehat{\mathrm{MCA}}$ (chứng minh trên)

Do đó, tam giác MAB đồng dạng với tam giác MCA (góc – góc) $\Rightarrow \frac{\mathrm{MA}}{\mathrm{MB}}=\frac{\mathrm{MC}}{\mathrm{MA}}$

$\Rightarrow {\mathrm{MA}}^2=\mathrm{MB}.\mathrm{MC}$ (đcpcm).

Bài tập 23 trang 76 SGK Toán lớp 9 tập 2: Cho đường tròn (O) và một điểm M cố định không nằm trên đường tròn. Qua M kẻ hai đường thẳng. Đường thẳng thứ nhất cắt (O) tại A và B. Đường thẳng thứ hai cắt (O) tại C và D. Chứng minh: MA.MB = MC.MD.

Hướng dẫn. Xét cả hai trường hợp điểm M nằm bên trong và bên ngoài đường tròn. Trong mỗi trường hợp, xét hai tam giác đồng dạng.

Lời giải:

TH1: Điểm M nằm bên trong đường tròn

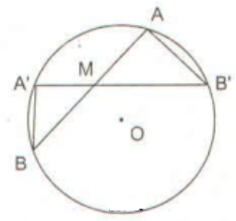
Xét đường tròn (O)

Góc AB’M là góc nội tiếp chắn cung nhỏ AA’

Góc A’BM là góc nội tiếp chắn cung nhỏ AA’ $\Rightarrow \widehat{\mathrm{AB}\text{'}\mathrm{M}}=\widehat{\mathrm{A}\text{'}\mathrm{BM}}$

Xét tam giác MAB’ và tam giác MA’B có:

$\widehat{\mathrm{A}\text{'}\mathrm{MB}}=\widehat{\mathrm{AMB}\text{'}}$ (hai góc đối đỉnh)

$\widehat{\mathrm{AB}\text{'}\mathrm{M}}=\widehat{\mathrm{A}\text{'}\mathrm{BM}}$ (chứng minh trên)

Do đó, tam giác MAB’ đồng dạng với tam giác MA’B (góc – góc)

$\Rightarrow \frac{\mathrm{MA}}{\mathrm{MA}\text{'}}=\frac{\mathrm{MB}\text{'}}{\mathrm{MB}}$

$\Rightarrow \mathrm{MA}.\mathrm{MB}=\mathrm{MB}\text{'}.\mathrm{MA}\text{'}$ (đcpcm)

TH2: Điểm M nằm bên ngoài đường tròn

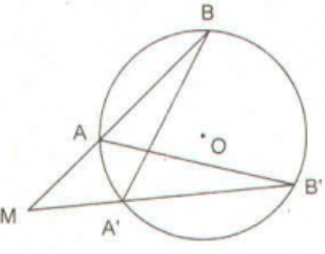
Góc AB’M là góc nội tiếp chắn cung nhỏ AA’

Góc A’BM là góc nội tiếp chắn cung nhỏ AA’

$\Rightarrow \widehat{\mathrm{AB}\text{'}\mathrm{M}}=\widehat{\mathrm{A}\text{'}\mathrm{BM}}$

Xét tam giác MAB’ và tam giác MA’B có:

$\widehat{\mathrm{AB}\text{'}\mathrm{M}}=\widehat{\mathrm{A}\text{'}\mathrm{BM}}$ (chứng minh trên)

 chung

Do đó, tam giác MAB’ đồng dạng với tam giác MA’B (góc – góc)

Bài tập 24 trang 76 SGK Toán lớp 9 tập 2: Một chiếc cầu được thiết kế như hình 21 có độ dài AB = 40m, chiều cao MK = 3m. Hãy tính bán kính của đường tròn chứa cung AMB.

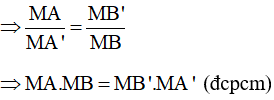
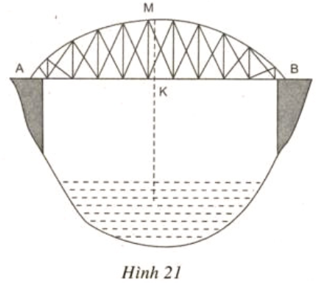
Lời giải:

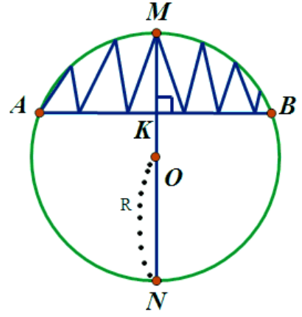
Chiếc cầu là cung của đường tròn tâm O bán kính R

Kẻ đường kính MN vuông góc với AB tại K

Theo định lý về đường kính và dây cung ta có: K là trung điểm của AB nên ta có:

KA = KB = 20m

Do MN vuông góc với AB tại K  nên ta có:

$\widehat{AKM}=\widehat{BKN}={90}^o$

Trong đường tròn (O), góc MAK và góc BNK là các góc nội tiếp cùng chắn cung nhỏ BM

$\Rightarrow \widehat{MAK}=\widehat{BNK}$

Xét tam giác KAM và tam giác KNB có:

$\widehat{AKM}=\widehat{BKN}={90}^o$ (chứng minh trên)

 $\widehat{MAK}=\widehat{BNK}$ (chứng minh trên)

Do đó, tam giác KAM đồng dạng với tam giác KNB (góc – góc) $\Rightarrow \frac{KA}{KN}=\frac{KM}{KB}$

Mà:

KA = KB = 20m

KM = 3m

KN = MN – KM = 2R – 3 (do MN là đường kính của đường tròn (O;R))

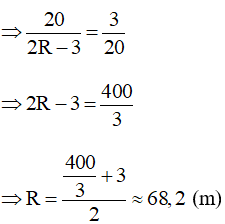
Vậy bán kính đường tròn chứa cung AMB dài 68,2 m.

Bài tập 25 trang 76 SGK Toán lớp 9 tập 2: Dựng một tam giác vuông, biết cạnh huyền dài 4cm và một cạnh góc vuông dài 2,5cm.

Lời giải:

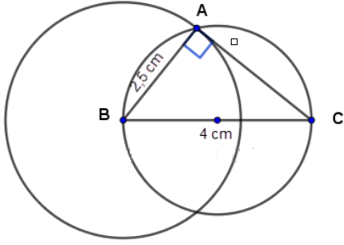
Cách dựng:

- Dựng đường tròn (O) có đường kính  BC bằng 4cm.

- Vẽ đường tròn tâm B bán kính 2,5 cm.

- Hai đường tròn cắt nhau tại điểm A.

- Ta được tam giác ABC là tam giác cần dựng.

Chứng minh:

Trong đường tròn (O), góc BAC là góc nội tiếp chắn nửa đường tròn $\Rightarrow \widehat{BAC}={90}^o$

Xét tam giác ABC có $\widehat{BAC}={90}^o$

Do đó, ABC là tam giác vuông tại A có:

BC = 4cm

BA = 2,5cm (do A nằm trên đường tròn (B; 2,5cm)).

Bài tập 26 trang 76 SGK Toán lớp 9 tập 2: Cho AB, BC, CA là ba dây của đường tròn (O). Từ điểm chính giữa M của cung AB vẽ dây MN song song với dây BC. Gọi giao điểm của MN và AC là S. Chứng minh SM = SC và SN = SA.

Lời giải:

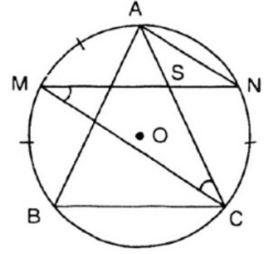
Xét đường tròn (O)

Theo giả thiết, ta có: M là điểm chính giữa cung AB

$\Rightarrow \stackrel{⏜}{MA}=\stackrel{⏜}{MB}$ (1)

Mặt khác, ta có: MN // BC

$\Rightarrow \stackrel{⏜}{MB}=\stackrel{⏜}{NC}$ (2) (hai dây song song chắn hai cung bằng nhau)

Từ (1) và (2) ta suy ra:

$\stackrel{⏜}{MA}=\stackrel{⏜}{NC}$ (3)

Mà ta có:

Góc MCA là góc nội tiếp chắn cung MA

Góc NMC là góc nội tiếp chắn cung NC

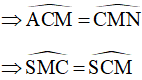
Xét tam giác SMC có: $\widehat{SMC}=\widehat{SCM}$

Do đó, tam giác SMC cân tại S

$\Rightarrow$ SM = SC.

Mặt khác, ta lại có:

Góc ANM là góc nội tiếp chắn cung MA (4)

Góc NAC là góc nội tiếp chắn cung NC (5)

Từ (3), (4), (5) ta suy ra:

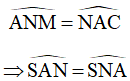
Xét tam giác SAN có: $\widehat{SAN}=\widehat{SNA}$

Do đó, tam giác SAN cân tại S

$\Rightarrow$ SA = SN.