Tailieumoi.vn xin giới thiệu Bài tập Toán 9 Chương 3 Bài 3: Góc nội tiếp. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 3 Bài 3: Góc nội tiếp. Mời các bạn đón xem:
Bài tập Toán 9 Chương 3 Bài 3: Góc nội tiếp
A. Bài tập Góc nội tiếp
I. Bài tập trắc nghiệm
Câu 1: Hình nào dưới đây biểu diễn góc nội tiếp?
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Lời giải:
Chọn đáp án B
Câu 2: Góc nội tiếp nhỏ hơn hoặc bằng 90° có số đo
A. Bằng nửa số đo góc ở tâm cùng chắn một cung
B. Bằng số đo góc ở tâm cùng chắn một cung
C. Bằng số đo cung bị chắn
D. Bằng nửa số đo cung lớn
Lời giải:
Trong một đường tròn:
Góc nội tiếp (nhỏ hơn hoặc bằng 90°) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung
Chọn đáp án A
Câu 3: Khẳng định nào sau đây là sai?
A. Trong một đường tròn, góc nội tiếp chắn nửa đường tròn là góc vuông
B. Trong một đường tròn, hai góc nội tiếp bằng nhau chắn hai cung bằng nhau
C. Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau
D. Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung
Lời giải:
Trong một đường tròn:
+ Các góc nội tiếp bằng nhau chắn các cung bằng nhau
+ Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau
+ Góc nội tiếp chắn nửa đường tròn là góc vuông
Như vậy hai góc nội tiếp bằng nhau có thể cùng chắn một cung hoặc chắn các cung bằng nhau
Phương án A, B, C đúng và D sai
Chọn đáp án D
Câu 4: Cho đường tròn (O) và điểm I nằm ngoài (O) . Từ điểm I kẻ hai dây cung AB và CD (A nằm giữa I và B, C nằm giữa I và D)
Cặp góc nào sau đây bằng nhau?
Chọn đáp án A
Câu 5: Cho đường tròn (O) và điểm I nằm ngoài (O). Từ điểm I kẻ hai dây cung AB và CD (A nằm giữa I và B, C nằm giữa I và D)
Tích IA.IB bằng
A. ID.CD
B. IC.CB
C. IC.CD
D. ID.ID
Chọn đáp án D
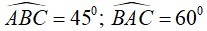
Tính số đo của 
A. 150°
B.90°
C. 120°
D. 210°
Tổng số đo 3 góc của 1 tam giác bằng 180° nên :
Chọn đáp án A
Câu 7: Cho tam giác ABC cân tại A có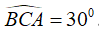 
. Tìm khẳng định đúng ?
Chọn đáp án A
Câu 8: Cho đường tròn tâm O và 2 đường kính AB và CD. Biết rằng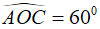 
. Tìm khẳng định sai ?
Ta có:
Chọn đáp án B
Câu 9: Cho tam giác ABC vuông tại A nội tiếp đường tròn (O; 4) .Biết rằng AC = 4cm . Lấy D là điểm bất kì khác A, B,C trên đường tròn. Chọn khẳng định sai ?
Chọn đáp án C.
Câu 10: Cho đường tròn tâm O. Trên đường tròn lấy 4 điểm phân biệt A,B, C và D. Hỏi cặp góc nào sau đây bằng nhau
Chọn đáp án D.
Câu 11: Cho đường tròn (O) và hai dây cung AB, AC bằng nhau. Qua A vẽ một cát tuyến cắt dây BC ở D và cắt (O) ở E. Khi đó DA. DE bằng
A. DC2
B. DB2
C. DB. DC
D. AB.AC
Xét (O) có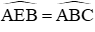 
(hai góc nội tiếp chắn hai cung bằng nhau AB = AC)
Xét ∆ADC và ∆BDE có:
Nên ∆ADC ~ ∆BDE (g − g)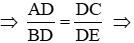 
DA. DE = DB. DC
Đáp án cần chọn là: C
Câu 12: Cho tam giác ABC nhọn nội tiếp (O). Hai đường cao BD và CE cắt nhau tại H. Vẽ đường kính AF. Hai đoạn thẳng nào sau đây bằng nhau?
A. BF = FC
B. BH = HC
C. BF = CH
D. BF = BH
Xét (O) có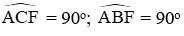 
(góc nội tiếp chắn nửa đường tròn)
Suy ra CF ⊥ AC; BF ⊥ AB mà BD ⊥ AC; CE ⊥ AB ⇒ BD // CF; CE // BF
⇒ BHCF là hình bình hành ⇒ BH = CF; BF = CH
Đáp án cần chọn là: C
Câu 13: Cho tam giác ABC nhọn nội tiếp (O). Hai đường cao BD và CE cắt nhau tại H. Vẽ đường kính AF. Chọn câu đúng:
A. BH = BE
B. BH = CF
C. BH = HC
D. HF = BC
Xét (O) có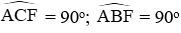 
(góc nội tiếp chắn nửa đường tròn)
Suy ra CF ⊥ AC; BF ⊥ AB mà BD ⊥ AC; CE ⊥ AB ⇒ BD // CF; CE // BF
⇒ BHCF là hình bình hành BH = CF
Đáp án cần chọn là: B
Câu 14: Cho (O), đường kính AB, điểm D thuộc đường tròn. Gọi E là điểm đối xứng với A qua D. Tam giác ABE là tam giác gì?
A. ∆BAE cân tại E
B. ∆BAE cân tại A
C. ∆BAE cân tại B
D. ∆BAE đều
Xét (O) có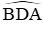 
= 90o (góc nội tiếp chắn nửa đường tròn) nên BD ⊥ EA mà D là trung điểm EA
Nên ∆BEA có BD vừa là đường cao vừa là đường trung tuyến ⇒ ∆BAE cân tại B
Đáp án cần chọn là: C
Câu 15: Cho (O), đường kính AB, điểm D thuộc đường tròn sao cho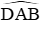 
= 50o. Gọi E là điểm đối xứng với A qua D. Góc AEB bằng bao nhiêu độ?
A. 50o
B. 60o
C. 45o
D. 70o
Xét (O) có 
= 90o (góc nội tiếp chắn nửa đường tròn) nên BD ⊥ EA mà D là trung điểm EA nên ∆BEA có BD vừa là đường cao vừa là đường trung tuyến nên ∆BAE cân tại B
Đáp án cần chọn là: A
II. Bài tập tự luận có lời giải
Câu 1: Cho tam giác ABC cân tại A (∠A = 90°). Vẽ đường tròn đường kính AB cắt BC tại D, cắt AC tại E. Chứng minh rằng: Tam giác DBE cân.
Lời giải:
Ta có:
+ ∠BDA = 90° (vì ∠BDA là góc nội tiếp chắn nửa đường tròn)
⇒ AD ⊥ BC
Mà ΔABC cân tại A nên AD vừa là đường cao vừa là đường phân giác góc A.
Khi đó ta có:
III. Bài tập vận dụng
Câu 1: Cho đường tròn (O; R) đường kính BC cố định. Điểm A di động trên đường tròn khác B và C. Vẽ đường kính AOD. Xác định vị trí điểm A để diện tích ΔABC đạt giá trị lớn nhất, khi đó 
Câu 2: Cho nửa đường tròn đường kính AB = 2m, dây CD // AB (C ∈ AD⌢). Tính độ dài các cạnh của hình thang ABCD biết chu vi hình thang bằng 5cm.
B. Lý thuyết Góc nội tiếp
1. Định nghĩa
- Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
- Cung bị chắn là cung nằm bên trong góc.
Ví dụ 1. Cho đường tròn (O) và hai dây cung AB, AC.
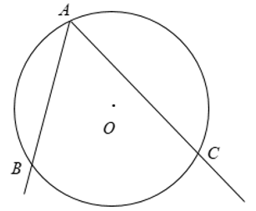
Khi đó, là góc nội tiếp và cung bị chắn là cung nhỏ BC.
2. Định lí
Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
Ví dụ 2. Cho đường tròn (O) có là góc nội tiếp chắn cung nhỏ BC (như hình 1) và chắn cung lớn BC (như hình 2).
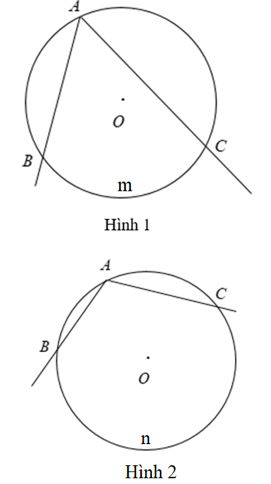
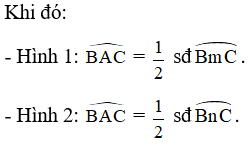
3. Hệ quả
Trong một đường tròn:
- Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
- Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
- Góc nội tiếp (nhỏ hơn hoặc bằng 90°) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
- Góc nội tiếp chắn nửa đường tròn là góc vuông.
Ví dụ 3. Cho đường tròn (O) và là góc nội tiếp chắn nửa đường tròn (O) (như hình vẽ).
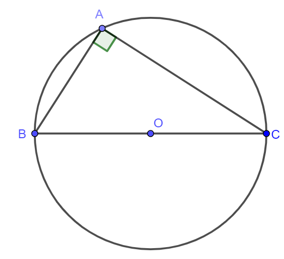
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
