Với giải Bài 19 trang 75 Toán lớp 9 chi tiết trong Bài 3: Góc nội tiếp giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán lớp 9 Bài 3: Góc nội tiếp
Bài tập 19 trang 75 SGK Toán lớp 9 tập 2: Cho đường tròn tâm O, đường kính AB và S là một điểm nằm bên ngoài đường tròn. SA và SB lần lượt cắt đường tròn tại M, N. Gọi H là giao điểm của BM và AN. Chứng minh rằng SH vuông góc với AB.
Lời giải:
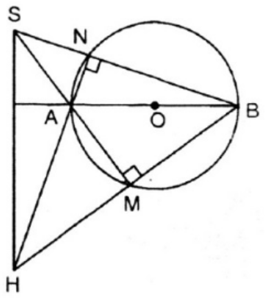
Trong đường tròn (O), là góc nội tiếp chắn nửa đường tròn (O) nên ta có:
tại M
tại M
Trong đường tròn (O), là góc nội tiếp chắn nửa đường tròn (O) nên ta có:
tại N
tại N
Xét tam giác SAB có:
tại M
tại N
Do đó, BM và AN là hai đường cao của tam giác SAB
Mà BM cắt AN tại H
Do đó, H là trực tâm của tam giác SAB
(đcpcm).
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
