Tailieumoi.vn xin giới thiệu Giải bài tập Toán 9 Bài 3: Giải hệ phương trình bằng phương pháp thế hay, chi tiết giúp học sinh dễ dàng làm bài tập Giải hệ phương trình bằng phương pháp thế lớp 9.

Giải bài tập Toán lớp 9 Bài 3: Giải hệ phương trình bằng phương pháp thế

Trả lời câu hỏi giữa bài

Câu hỏi 1 trang 14 Toán 9 Tập 2: Giải hệ phương trình sau bằng phương pháp thế (biểu diễn y theo x từ phương trình thứ hai của hệ)

Lời giải:

$\left\{\begin{array}{l}4x-5y=3\\ 3x-y=16\end{array}\right.\iff \left\{\begin{array}{l}4x-5y=3\text{ (1)}\\ y=3x-16\text{ (2)}\end{array}\right.$

Thay (2) vào (1) ta được:

$$\begin{gathered} \left\{\begin{array}{l}4x-5\left(3x-16\right)=3\\ y=3x-16\end{array}\right. \\ \iff \left\{\begin{array}{l}4x-15x+80=3\\ y=3x-16\end{array}\right. \\ \iff \left\{\begin{array}{l}-11x=3-80\\ y=3x-16\end{array}\right. \\ \iff \left\{\begin{array}{l}-11x=-77\\ y=3x-16\end{array}\right. \\ \iff \left\{\begin{array}{l}x=(-77):(-11)\\ y=3x-16\end{array}\right. \\ \iff \left\{\begin{array}{l}x=7\\ y=3.7-16\end{array}\right. \\ \iff \left\{\begin{array}{l}x=7\\ y=5\end{array}\right. \end{gathered}$$

Vậy hệ phương trình có nghiệm duy nhất (x; y) = (7; 5)

Câu hỏi 2 trang 15 Toán 9 Tập 2: Bằng minh họa hình học, hãy giải thích tại sao hệ (III) có vô số nghiệm.

Lời giải:

$\left\{\begin{array}{l}4x-2y=-6\\ -2x+y=3\end{array}\right.\left(III\right)$

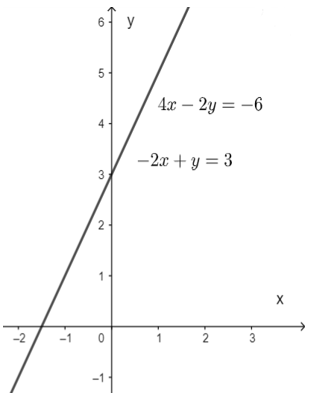
Vẽ đường thẳng 4x – 2y = -6

Cho x = 0 $\Rightarrow y = 3\Rightarrow$(0; 3)

Cho y = 0 $\Rightarrow x=\frac{-3}{2}\Rightarrow \left(\frac{-3}{2};0\right)$

Đường thẳng 4x - 3y = -6 đi qua hai điểm (0; 3) và $\left(\frac{-3}{2};0\right)$

Vẽ đường thẳng -2x + y = 3

Cho x = 0 $\Rightarrow y = 3\Rightarrow$(0; 3)

Cho y = 0$\Rightarrow x=\frac{-3}{2}\Rightarrow \left(\frac{-3}{2};0\right)$

Đường thẳng -2x + y = 3 đi qua hai điểm (0; 3) và $\left(\frac{-3}{2};0\right)$

Từ đồ thị ta thấy đường thẳng trùng nhau nên hệ đã cho có vô số nghiệm.

Câu hỏi 3 trang 15 Toán 9 Tập 2: Cho hệ phương trình:

$\left(IV\right)\left\{\begin{array}{l}4x+y=2\\ 8x+2y=1\end{array}\right.$

Bằng minh họa hình học và bằng phương pháp thế, chứng tỏ rằng hệ (IV) vô nghiệm.

Lời giải:

*) Bằng minh họa hình học

- Xét đường thẳng (d): 4x + y = 2 hay y = -4x + 2

Cho x = 0 $\Rightarrow y=2\Rightarrow \left(0;2\right)$

Cho y = 0$\Rightarrow x=\frac{1}{2}\Rightarrow \left(\frac{1}{2};0\right)$

Đường thẳng (d) đi qua hai điểm (0; 2) và $\left(\frac{1}{2};0\right)$

- Xét đường thẳng (d’): 8x + 2y = 1 hay y = -4x +$\frac{1}{2}$

Cho x = 0 $\Rightarrow y=\frac{1}{2}\Rightarrow \left(0;\frac{1}{2}\right)$

Cho y = 0 $\Rightarrow x=\frac{1}{8}\Rightarrow \left(\frac{1}{8};0\right)$

Đường thẳng (d’) đi qua hai điểm $\left(0;\frac{1}{2}\right)$ và $\left(\frac{1}{8};0\right)$

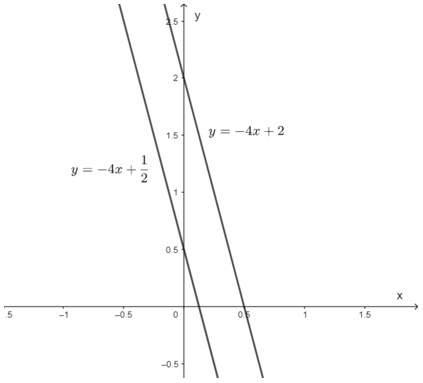
Từ hình vẽ trên ta thấy hai đường thẳng đã cho song song nên hệ phương trình vô nghiệm.

*) Bằng phương pháp thế:

$$\begin{gathered} \left(IV\right)\left\{\begin{array}{l}4x+y=2\\ 8x+2y=1\end{array}\right. \\ \iff \left\{\begin{array}{l}y=2-4x\\ 8x+2\left(2-4x\right)=1\end{array}\right. \end{gathered}$$

$$\begin{gathered} \iff \left\{\begin{array}{l}8x+4-8x=1\\ y=2-4x\end{array}\right. \\ \iff \left\{\begin{array}{l}4=1\\ y=2-4x\end{array}\right.(Vô lí) \end{gathered}$$

Vậy hệ đã cho vô nghiệm

Bài tập (trang 15)

Bài 12 trang 15 SGK Toán 9 Tập 2: Giải các hệ phương trình sau bằng phương pháp thế:

a) $\left\{\begin{array}{l}x-y=3\\ 3x-4y=2\end{array}\right.$

b) $\left\{\begin{array}{l}7x-3y=5\\ 4x+y=2\end{array}\right.$

c) $\left\{\begin{array}{l}x+3y=-2\\ 5x-4y=11\end{array}\right.$

Lời giải:

a)

$$\begin{gathered} \left\{\begin{array}{l}x-y=3\\ 3x-4y=2\end{array}\right. \\ \iff \left\{\begin{array}{l}x=3+y\\ 3x-4y=2\end{array}\right. \\ \iff \left\{\begin{array}{l}x=3+y\\ 3\left(3+y\right)-4y=2\end{array}\right. \\ \iff \left\{\begin{array}{l}x=3+y\\ 9+3y-4y=2\end{array}\right. \\ \iff \left\{\begin{array}{l}x=3+y\\ 9+3y-4y=2\end{array}\right. \\ \iff \left\{\begin{array}{l}x=y+3\\ y=9-2\end{array}\right. \\ \iff \left\{\begin{array}{l}x=y+3\\ y=7\end{array}\right. \\ \iff \left\{\begin{array}{l}x=7+3\\ y=7\end{array}\right. \\ \iff \left\{\begin{array}{l}x=10\\ y=7\end{array}\right. \end{gathered}$$

Vậy hệ phương trình đã cho có nghiệm (x; y) = (10; 7)

b)

$$\begin{gathered} \left\{\begin{array}{l}7x-3y=5\\ 4x+y=2\end{array}\right. \\ \iff \left\{\begin{array}{l}7x-3y=5\\ y=2-4x\end{array}\right. \\ \iff \left\{\begin{array}{l}7x-3.\left(2-4x\right)=5\\ y=2-4x\end{array}\right. \\ \iff \left\{\begin{array}{l}7x-6+12x=5\\ y=2-4x\end{array}\right. \\ \iff \left\{\begin{array}{l}19x=5+6\\ y=2-4x\end{array}\right. \\ \iff \left\{\begin{array}{l}19x=11\\ y=2-4x\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\frac{11}{19}\\ y=2-4.\frac{11}{19}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\frac{11}{19}\\ y=\frac{-6}{19}\end{array}\right. \end{gathered}$$

Vậy hệ phương trình đã cho có nghiệm (x; y) = $\left(\frac{11}{19};\frac{-6}{19}\right)$.

c)

$$\begin{gathered} \left\{\begin{array}{l}x+3y=-2\\ 5x-4y=11\end{array}\right. \\ \iff \left\{\begin{array}{l}x=-2-3y\\ 5\left(-2-3y\right)-4y=11\end{array}\right. \\ \iff \left\{\begin{array}{l}x=-2-3y\\ -10-15y-4y=11\end{array}\right. \\ \iff \left\{\begin{array}{l}x=-2-3y\\ -19y=10+11\end{array}\right. \\ \iff \left\{\begin{array}{l}x=-2-3y\\ -19y=21\end{array}\right. \\ \iff \left\{\begin{array}{l}x=-2-3y\\ y=\frac{-21}{19}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=-2-3.\left(\frac{-21}{19}\right)\\ y=\frac{-21}{19}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\frac{25}{19}\\ y=\frac{-21}{19}\end{array}\right. \end{gathered}$$

Vậy hệ phương trình đã cho có nghiệm (x; y) = $\left(\frac{25}{19};\frac{-21}{19}\right)$.

Bài 13 trang 15 SGK Toán 9 Tập 2: Giải các hệ phương trình sau bằng phương pháp thế:

a) $\left\{\begin{array}{l}3x-2y=11\\ 4x-5y=3\end{array}\right.$

b) $\left\{\begin{array}{l}\frac{x}{2}-\frac{y}{3}=1\\ 5x-8y=3\end{array}\right.$

Lời giải:

a)

$$\begin{gathered} \left\{\begin{array}{l}3x-2y=11\\ 4x-5y=3\end{array}\right. \\ \iff \left\{\begin{array}{l}3x=11+2y\\ 4x-5y=3\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\frac{11+2y}{3}\\ 4x-5y=3\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\frac{11+2y}{3}\\ 4.\frac{11+2y}{3}-5y=3\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\frac{11+2y}{3}\\ \frac{44+8y}{3}-5y=3\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\frac{11+2y}{3}\\ 44+8y-15y=9\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\frac{11+2y}{3}\\ 7y=35\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\frac{11+2.5}{3}\\ y=5\end{array}\right. \\ \iff \left\{\begin{array}{l}x=7\\ y=5\end{array}\right. \end{gathered}$$

Vậy hệ phương trình đã cho có nghiệm (x; y) là (7; 5)

b)

$$\begin{gathered} \left\{\begin{array}{l}\frac{x}{2}-\frac{y}{3}=1\\ 5x-8y=3\end{array}\right. \\ \iff \left\{\begin{array}{l}\frac{x}{2}=1+\frac{y}{3}\\ 5x-8y=3\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\left(1+\frac{y}{3}\right).2\\ 5x-8y=3\end{array}\right. \\ \iff \left\{\begin{array}{l}x=2+\frac{2}{3}y\\ 5\left(2+\frac{2}{3}y\right)-8.y=3\end{array}\right. \\ \iff \left\{\begin{array}{l}x=2+\frac{2}{3}y\\ 10+\frac{10}{3}y-8y=3\end{array}\right. \\ \iff \left\{\begin{array}{l}x=2+\frac{2}{3}y\\ \frac{-14}{3}y=3-10\end{array}\right. \\ \iff \left\{\begin{array}{l}x=2+\frac{2}{3}y\\ \frac{-14}{3}y=-7\end{array}\right. \\ \iff \left\{\begin{array}{l}x=2+\frac{{\displaystyle 2}}{{\displaystyle 3}}y\\ y=\left(-7\right):\left(\frac{{\displaystyle -14}}{{\displaystyle 3}}\right)\end{array}\right. \\ \iff \left\{\begin{array}{l}x=2+\frac{{\displaystyle 2}}{{\displaystyle 3}}y\\ y=\frac{{\displaystyle 3}}{{\displaystyle 2}}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=2+\frac{{\displaystyle 2}}{{\displaystyle 3}}.\frac{{\displaystyle 3}}{{\displaystyle 2}}\\ y=\frac{{\displaystyle 3}}{{\displaystyle 2}}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=3\\ y=\frac{{\displaystyle 3}}{{\displaystyle 2}}\end{array}\right. \end{gathered}$$

Vậy hệ phương trình đã cho có nghiệm (x; y) = $\left(3;\frac{3}{2}\right)$.

Bài 14 trang 15 SGK Toán 9 Tập 2: Giải các hệ phương trình sau bằng phương pháp thế:

a) $\left\{\begin{array}{l}x+y\sqrt{5}=0\\ x\sqrt{5}+3y=1-\sqrt{5}\end{array}\right.$

b) $\left\{\begin{array}{l}\left(2-\sqrt{3}\right)x-3y=2+5\sqrt{3}\\ 4x+y=4-2\sqrt{3}\end{array}\right.$

Lời giải:

a) 

$$\begin{gathered} \left\{\begin{array}{l}x+y\sqrt{5}=0\\ x\sqrt{5}+3y=1-\sqrt{5}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=-y\sqrt{5}\\ -y\sqrt{5}.\sqrt{5}+3y=1-\sqrt{5}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=-y\sqrt{5}\\ y\left(-5+3\right)=1-\sqrt{5}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=-y\sqrt{5}\\ -2y=1-\sqrt{5}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=-\sqrt{5}y\\ y=\frac{1-\sqrt{5}}{-2}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=-\sqrt{5}y\\ y=\frac{\sqrt{5}-1}{2}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=-\sqrt{5}.\left(\frac{\sqrt{5}-1}{2}\right)\\ y=\frac{\sqrt{5}-1}{2}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\frac{\sqrt{5}-5}{2}\\ y=\frac{\sqrt{5}-1}{2}\end{array}\right. \end{gathered}$$

Vậy hệ phương trình đã cho có nghiệm (x; y) =$\left(\frac{\sqrt{5}-5}{2};\frac{\sqrt{5}-1}{2}\right)$

b)

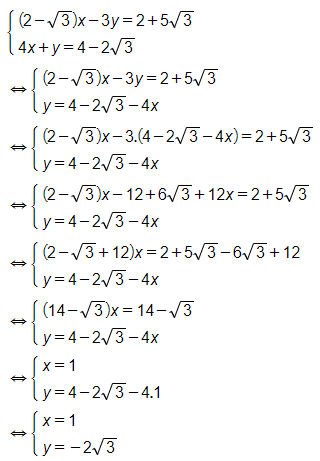
Vậy phương trình đã cho có nghiệm (x; y) là (1; $-2\sqrt{3}$).

Luyện tập trang 15, 16

Bài 15 trang 15 SGK Toán 9 Tập 2: Giải hệ phương trình $\left\{\begin{array}{l}x+3y=1\\ \left(a^2+1\right)x+6y=2a\end{array}\right.$ trong mỗi trường hợp sau:

a) a = -1;

b) a = 0;

c) a = 1.

Lời giải:

$\left\{\begin{array}{l}x+3y=1\\ \left(a^2+1\right)x+6y=2a\end{array}\right.$$\iff \left\{\begin{array}{l}x=1-3y\\ \left(a^2+1\right)\left(1-3y\right)+6y=2a\end{array}\right.$

a) Thay a = -1 vào hệ phương trình ta được

$$\begin{gathered} \left\{\begin{array}{l}x=1-3y\\ \left({\left(-1\right)}^2+1\right)\left(1-3y\right)+6y=2.\left(-1\right)\end{array}\right. \\ \iff \left\{\begin{array}{l}x=1-3y\\ 2.\left(1-3y\right)+6y=-2\end{array}\right. \\ \iff \left\{\begin{array}{l}x=1-3y\\ 2-6y+6y=-2\end{array}\right. \end{gathered}$$

$\iff \left\{\begin{array}{l}x=1-3y\\ 2=-2\end{array}\right.$ (vô lí)

Vậy với a = - 1 hệ phương trình đã cho vô nghiệm.

b) Thay a = 0 vào hệ phương trình ta được

$$\begin{gathered} \left\{\begin{array}{l}x=1-3y\\ \left(0^2+1\right)\left(1-3y\right)+6y=2.0\end{array}\right. \\ \iff \left\{\begin{array}{l}x=1-3y\\ 1-3y+6y=0\end{array}\right. \\ \iff \left\{\begin{array}{l}x=1-3y\\ 3y=-1\end{array}\right. \\ \iff \left\{\begin{array}{l}x=1-3y\\ y=\frac{-1}{3}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=1-3.\left(\frac{-1}{3}\right)\\ y=\frac{-1}{3}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=2\\ y=\frac{-1}{3}\end{array}\right. \end{gathered}$$

Vậy với a = 0 hệ phương trình đã cho có nghiệm duy nhất (x; y) =$\left(2;\frac{-1}{3}\right)$

c) Thay a = 1 vào hệ phương trình ta có:

$$\begin{gathered} \left\{\begin{array}{l}x=1-3y\\ \left(1^2+1\right)\left(1-3y\right)+6y=2.1\end{array}\right. \\ \iff \left\{\begin{array}{l}x=1-3y\\ 2.\left(1-3y\right)+6y=2\end{array}\right. \\ \iff \left\{\begin{array}{l}x=1-3y\\ 2-6y+6y=2\end{array}\right. \end{gathered}$$

$\iff \left\{\begin{array}{l}x=1-3y\\ 2=2\end{array}\right.$ (luôn đúng)

Vậy với a = 1 hệ phương trình đã cho có vô số nghiệm dạng (1 – 3y; y) với $y\in ℝ$

Bài 16 trang 16 SGK Toán 9 Tập 2: Giải các hệ phương trình sau bằng phương pháp thế:

a) $\left\{\begin{array}{l}3x-y=5\\ 5x+2y=23\end{array}\right.$

b) $\left\{\begin{array}{l}3x+5y=1\\ 2x-y=-8\end{array}\right.$

c) $\left\{\begin{array}{l}\frac{x}{y}=\frac{2}{3}\\ x+y-10=0\end{array}\right.$

Lời giải:

a)

$$\begin{gathered} \left\{\begin{array}{l}3x-y=5\\ 5x+2y=23\end{array}\right. \\ \iff \left\{\begin{array}{l}y=3x-5\\ 5x+2.\left(3x-5\right)=23\end{array}\right. \\ \iff \left\{\begin{array}{l}5x+6x-10=23\\ y=3x-5\end{array}\right. \\ \iff \left\{\begin{array}{l}11x=23+10\\ y=3x-5\end{array}\right. \\ \iff \left\{\begin{array}{l}11x=33\\ y=3x-5\end{array}\right. \\ \iff \left\{\begin{array}{l}x=33:11\\ y=3x-5\end{array}\right. \\ \iff \left\{\begin{array}{l}x=3\\ y=3.3-5\end{array}\right. \\ \iff \left\{\begin{array}{l}x=3\\ y=4\end{array}\right. \end{gathered}$$

Vậy hệ phương trình đã cho có nghiệm là (x; y) = (3; 4)

b)

$$\begin{gathered} \left\{\begin{array}{l}3x+5y=1\\ 2x-y=-8\end{array}\right. \\ \iff \left\{\begin{array}{l}3x+5y=1\\ y=2x+8\end{array}\right. \\ \iff \left\{\begin{array}{l}3x+5\left(2x+8\right)=1\\ y=2x+8\end{array}\right. \\ \iff \left\{\begin{array}{l}3x+10x+40=1\\ y=2x+8\end{array}\right. \\ \iff \left\{\begin{array}{l}13x=1-40\\ y=2x+8\end{array}\right. \\ \iff \left\{\begin{array}{l}13x=-39\\ y=2x+8\end{array}\right. \\ \iff \left\{\begin{array}{l}x=-39:13\\ y=2x+8\end{array}\right. \\ \iff \left\{\begin{array}{l}x=-3\\ y=2.\left(-3\right)+8\end{array}\right. \\ \iff \left\{\begin{array}{l}x=-3\\ y=2\end{array}\right. \end{gathered}$$

Vậy hệ phương trình đã cho có nghiệm duy nhất (x; y) = (-3; 2).

c)

$$\begin{gathered} \left\{\begin{array}{l}\frac{x}{y}=\frac{2}{3}\\ x+y-10=0\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\frac{2}{3}y\\ \frac{2}{3}y+y-10=0\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\frac{2}{3}y\\ \frac{5}{3}y=10\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\frac{2}{3}y\\ y=10:\frac{5}{3}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\frac{2}{3}y\\ y=6\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\frac{2}{3}.6\\ y=6\end{array}\right. \\ \iff \left\{\begin{array}{l}x=4\\ y=6\end{array}\right. \end{gathered}$$

Vậy hệ phương trình đã cho có nghiệm (x; y) = (4; 6).

Bài 17 trang 16 SGK Toán 9 Tập 2: Giải các hệ phương trình sau bằng phương pháp thế:

a) $\left\{\begin{array}{l}x\sqrt{2}-y\sqrt{3}=1\\ x+y\sqrt{3}=\sqrt{2}\end{array}\right.$

b) $\left\{\begin{array}{l}x-2\sqrt{2}y=\sqrt{5}\\ x\sqrt{2}+y=1-\sqrt{10}\end{array}\right.$

c) $\left\{\begin{array}{l}\left(\sqrt{2}-1\right)x-y=\sqrt{2}\\ x+\left(\sqrt{2}+1\right)y=1\end{array}\right.$

Lời giải:

a)

$$\begin{gathered} \left\{\begin{array}{l}x\sqrt{2}-y\sqrt{3}=1\\ x+y\sqrt{3}=\sqrt{2}\end{array}\right. \\ \iff \left\{\begin{array}{l}x\sqrt{2}-y\sqrt{3}=1\\ x=\sqrt{2}-y\sqrt{3}\end{array}\right. \\ \iff \left\{\begin{array}{l}\left(\sqrt{2}-y\sqrt{3}\right)\sqrt{2}-y\sqrt{3}=1\\ x=\sqrt{2}-y\sqrt{3}\end{array}\right. \\ \iff \left\{\begin{array}{l}2-y\sqrt{6}-y\sqrt{3}=1\\ x=\sqrt{2}-y\sqrt{3}\end{array}\right. \\ \iff \left\{\begin{array}{l}y\left(-\sqrt{6}-\sqrt{3}\right)=1-2\\ x=\sqrt{2}-y\sqrt{3}\end{array}\right. \\ \iff \left\{\begin{array}{l}y\left(\sqrt{6}+\sqrt{3}\right)=1\\ x=\sqrt{2}-y\sqrt{3}\end{array}\right. \\ \iff \left\{\begin{array}{l}y=\frac{1}{\sqrt{6}+\sqrt{3}}\\ x=\sqrt{2}-y\sqrt{3}\end{array}\right. \\ \iff \left\{\begin{array}{l}y=\frac{\sqrt{6}-\sqrt{3}}{3}\\ x=\sqrt{2}-\frac{\sqrt{6}-\sqrt{3}}{3}.\sqrt{3}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=1\\ y=\frac{\sqrt{6}-\sqrt{3}}{3}\end{array}\right. \end{gathered}$$

Vậy hệ phương trình đã cho có nghiệm (x; y) = $\left(1;\frac{\sqrt{6}-\sqrt{3}}{3}\right)$

b)

$$\begin{gathered} \left\{\begin{array}{l}x-2\sqrt{2}y=\sqrt{5}\\ x\sqrt{2}+y=1-\sqrt{10}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\sqrt{5}+2\sqrt{2}y\\ \left(\sqrt{5}+2\sqrt{2}y\right)\sqrt{2}+y=1-\sqrt{10}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\sqrt{5}+2\sqrt{2}y\\ \sqrt{10}+4y+y=1-\sqrt{10}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\sqrt{5}+2\sqrt{2}y\\ 5y=1-\sqrt{10}-\sqrt{10}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\sqrt{5}+2\sqrt{2}y\\ 5y=1-2\sqrt{10}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\sqrt{5}+2\sqrt{2}y\\ y=\frac{1-2\sqrt{10}}{5}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\sqrt{5}+2\sqrt{2}.\frac{1-2\sqrt{10}}{5}\\ y=\frac{1-2\sqrt{10}}{5}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\sqrt{5}+\frac{2\sqrt{2}-2\sqrt{2}.2\sqrt{10}}{5}\\ y=\frac{1-2\sqrt{10}}{5}\end{array}\right. \\ \iff \left\{\begin{array}{l}x=\frac{-3\sqrt{5}+2\sqrt{2}}{5}\\ y=\frac{1-2\sqrt{10}}{3}\end{array}\right. \end{gathered}$$

Vậy hệ phương trình đã cho có nghiệm (x; y) = $\left(\frac{-3\sqrt{5}+2\sqrt{2}}{5};\frac{1-2\sqrt{10}}{3}\right)$

c)

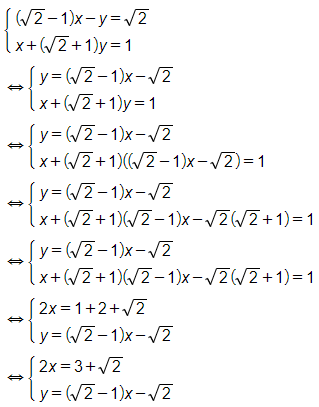
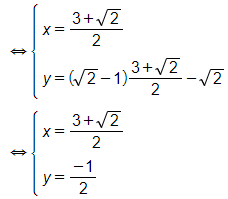
Vậy hệ phương trình đã cho có nghiệm (x; y) =$\left(\frac{3+\sqrt{2}}{2};\frac{-1}{2}\right)$

Bài 18 trang 16 SGK Toán 9 Tập 2: a) Xác định các hệ số a và b, biết rằng hệ phương trình $\left\{\begin{array}{l}2x+by=-4\\ bx-ay=-5\end{array}\right.$ có nghiệm (1; -2).

b) Cũng hỏi như vậy nếu phương trình có nghiệm là $\left(\sqrt{2}-1;\sqrt{2}\right)$

Lời giải:

a) Vì hệ phương trình có nghiệm (1; -2) nên x = 1 và y = -2 thỏa mãn cả hai phương trong trong hệ.

Thay x = 1 và y = -2 vào hệ ta được:

$$\begin{gathered} \left\{\begin{array}{l}2.1+b.(-2)=-4\\ b.1-a.(-2)=-5\end{array}\right. \\ \iff \left\{\begin{array}{l}2-2b=-4\\ b+2a=-5\end{array}\right. \\ \iff \left\{\begin{array}{l}-2b=-4-2\\ b+2a=-5\end{array}\right. \\ \iff \left\{\begin{array}{l}-2b=-6\\ b+2a=-5\end{array}\right. \\ \iff \left\{\begin{array}{l}b=3\\ 3+2a=-5\end{array}\right. \\ \iff \left\{\begin{array}{l}2a=-5-3\\ b=3\end{array}\right. \\ \iff \left\{\begin{array}{l}2a=-8\\ b=3\end{array}\right. \\ \iff \left\{\begin{array}{l}a=-4\\ b=3\end{array}\right. \end{gathered}$$

Vậy để hệ phương trình đã cho có nghiệm là (1; -2) thì a = -4 và b = 3.

b) Vì hệ phương trình có nghiệm $\left(\sqrt{2}-1;\sqrt{2}\right)$ nên x =$\sqrt{2}-1$  và y = $\sqrt{2}$ thỏa mãn cả hai phương trong trong hệ.

Thay x = $\sqrt{2}-1$ và y =$\sqrt{2}$ vào hệ ta được:

$\left\{\begin{array}{l}2.\left(\sqrt{2}-1\right)+b.\sqrt{2}=-4\\ b.\left(\sqrt{2}-1\right)-a.\sqrt{2}=-5\end{array}\right.$

$\iff \left\{\begin{array}{l}2\sqrt{2}-2+b\sqrt{2}=-4\\ b\left(\sqrt{2}-1\right)-a\sqrt{2}=-5\end{array}\right.$

$$\begin{gathered} \iff \left\{\begin{array}{l}b\sqrt{2}=-4+2-2\sqrt{2}\\ b\left(\sqrt{2}-1\right)-a\sqrt{2}=-5\end{array}\right. \\ \iff \left\{\begin{array}{l}\sqrt{2}b=-2-2\sqrt{2}\\ b\left(\sqrt{2}-1\right)-a\sqrt{2}=-5\end{array}\right. \end{gathered}$$

$$\begin{gathered} \iff \left\{\begin{array}{l}b=\frac{-2-2\sqrt{2}}{\sqrt{2}}\\ b\left(\sqrt{2}-1\right)-a\sqrt{2}=-5\end{array}\right. \\ \iff \left\{\begin{array}{l}b=-2-\sqrt{2}\\ b\left(\sqrt{2}-1\right)-a\sqrt{2}=-5\end{array}\right. \\ \iff \left\{\begin{array}{l}b=-2-\sqrt{2}\\ \left(-2-\sqrt{2}\right)\left(\sqrt{2}-1\right)-a\sqrt{2}=-5\end{array}\right. \end{gathered}$$

$$\begin{gathered} \iff \left\{\begin{array}{l}b=-2-\sqrt{2}\\ -2\sqrt{2}-2+2+\sqrt{2}-a\sqrt{2}=-5\end{array}\right. \\ \iff \left\{\begin{array}{l}b=-2-\sqrt{2}\\ -a\sqrt{2}=-5+2\sqrt{2}+2-2-\sqrt{2}\end{array}\right. \end{gathered}$$

$$\begin{gathered} \iff \left\{\begin{array}{l}b=-2-\sqrt{2}\\ -a\sqrt{2}=-5+\sqrt{2}\end{array}\right. \\ \iff \left\{\begin{array}{l}a=\frac{-5+\sqrt{2}}{-\sqrt{2}}\\ b=-2-\sqrt{2}\end{array}\right. \\ \iff \left\{\begin{array}{l}a=\frac{5\sqrt{2}-2}{2}\\ b=-2-\sqrt{2}\end{array}\right. \end{gathered}$$

Vậy để hệ phương trình đã cho có nghiệm là $\left(\sqrt{2}-1;\sqrt{2}\right)$ thì a =$\frac{5\sqrt{2}-2}{2}$ và b = -2 -$\sqrt{2}$

Bài 19 trang 16 SGK Toán 9 Tập 2: Biết rằng: Đa thức P(x) chia hết cho đa thức x – a khi và chỉ khi P(a) = 0. Hãy tìm các giá trị của m và n sao cho đa thức sau đồng thời chia hết cho x + 1 và x – 3:

P(x) = mx³ + (m – 2)x² – (3n – 5)x – 4n

Lời giải

+ P(x) chia hết cho x + 1

⇔ P(-1) = 0

⇔ m.(-1)³ + (m – 2)(-1)² – (3n – 5).(-1) – 4n = 0

⇔ -m + m – 2 + 3n – 5 – 4n = 0

⇔ -n – 7 = 0

⇔ n = -7 (1)

Vậy với mọi m và n = -7 thì P(x) chia hết cho x + 1

+ P(x) chia hết cho x – 3

⇔ P(3) = 0

⇔ m.3³ + (m – 2).3² – (3n – 5).3 – 4n = 0

⇔ 27m + 9m – 18 – 9n + 15 – 4n = 0

⇔ 36m – 13n = 3 (2)

Từ (1) và (2) ta có hệ phương trình:

$$\begin{gathered} \left\{\begin{array}{l}n=-7\\ 36m-13n=3\end{array}\right. \\ \iff \left\{\begin{array}{l}n=-7\\ 36m-13.\left(-7\right)=3\end{array}\right. \\ \iff \left\{\begin{array}{l}n=-7\\ 36m+91=3\end{array}\right. \\ \iff \left\{\begin{array}{l}n=-7\\ 36m=3-91\end{array}\right. \end{gathered}$$

$$\begin{gathered} \iff \left\{\begin{array}{l}n=-7\\ 36m=-88\end{array}\right. \\ \iff \left\{\begin{array}{l}n=-7\\ m=\frac{-22}{9}\end{array}\right. \end{gathered}$$

Vậy n = -7; m =$\frac{-22}{9}$  thì P(x) chia hết cho x – 3.