Giải Toán 7 trang 87 Tập 1 Kết nối tri thức

ndiep Ngày: 29-12-2022 Lớp 7

300

Với Giải toán lớp 7 trang 87 Tập 1 Kết nối tri thức chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:

Giải Toán 7 trang 87 Tập 1 Kết nối tri thức

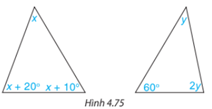
Bài 4.33 trang 87 Toán lớp 7: Tính các số đo x, y trong tam giác dưới đây (H.4.75)

Phương pháp giải:

Áp dụng tổng 3 góc của 1 tam giác bằng 180 độ.

Lời giải:

Áp dụng định lí tổng ba góc trong tam giác,

+) Ta có:

$\begin{array}{l} x + x + 20^{o} + x + 10^{o} = 180^{o} \\ \Rightarrow 3 x = 150^{o} \\ \Rightarrow x = 50^{o} \end{array}$

+) Ta có:

$\begin{array}{l} y + 60^{o} + 2 y = 180^{o} \\ \Rightarrow 3 y = 120^{o} \\ \Rightarrow y = 40^{o} \end{array}$

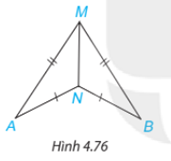
Bài 4.34 trang 87 Toán lớp 7: Trong Hình 4.76, có AM = BM, AN = BN. Chứng minh rằng $\hat{M A N} = \hat{M B N}$ .

Phương pháp giải:

Chứng minh 2 tam giác MNA và MNB bằng nhau từ đó suy ra 2 góc tương ứng bằng nhau.

Lời giải:

Xét 2 tam giác MNA và MNB có:

AM=BM

AN=BN

MN chung

=> $Δ M N A = Δ M N B$ (c.c.c)

=> $\hat{M A N} = \hat{M B N}$ (2 góc tương ứng)

Bài 4.35 trang 87 Toán lớp 7: Trong Hình 4.77, có AO = BO,

\hat{O A M} = \hat{O B N}

. Chứng minh rằng AM = BN.

Phương pháp giải:

Chứng minh 2 tam giác OAM và OBN bằng nhau từ đó suy ra AM=BN.

Lời giải:

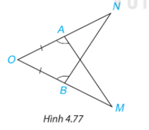
Xét 2 tam giác OAM và OBN có:

AO=BO

Góc O chung

=>(g.c.g)

=>AM=BN (2 cạnh tương ứng)

Bài 4.36 trang 87 Toán lớp 7: Trong Hình 4.78, ta có AN = BM, $\hat{B A N} = \hat{A B M}$ . Chứng minh rằng $\hat{B A M} = \hat{A B N}$ .

Phương pháp giải:

Chứng minh 2 tam giác ANB và BMA bằng nhau từ đó suy ra

\hat{B A M} = \hat{A B N}

Lời giải:

Xét hai tam giác BAM và ABN có:

AN=BM

$\hat{B A N} = \hat{A B M}$

AB chung

=> $Δ B A M = Δ A B N$ (c.g.c)

Vậy $\hat{B A M} = \hat{A B N}$ (2 góc tương ứng).

Bài 4.37 trang 87 Toán lớp 7: Cho M, N là hai điểm phân biệt nằm trên đường trung trực của đoạn thẳng AB sao cho AM = AN. Chứng minh rằng MB = NB và góc AMB bằng góc ANB.

Lời giải:

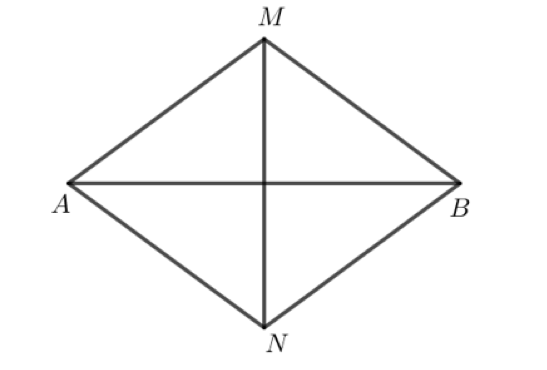
Toán lớp 7 Bài tập cuối chương 4 | Kết nối tri thức (ảnh 1)

Do M nằm trên đường trung trực của đoạn thẳng AB nên MA = MB.

Do N nằm trên đường trung trực của đoạn thẳng AB nên NA = NB.

Mà MA = NA (theo giải thiết có AM = AN) nên MA = MB = NA = NB.

Suy ra MB = NB.

Xét tam giác AMB và tam giác ANB có:

MA = NA (giả thiết)

MB = NB (chứng minh trên)

AB: cạnh chung

Do đó, ∆AMB = ∆ANB (c – c – c).

Suy ra $\hat{AMB} = \hat{ANB}$ (hai góc tương ứng).

Vậy MB = NB và $\hat{AMB} = \hat{ANB}$

Bài 4.38 trang 87 Toán lớp 7: Cho tam giác ABC cân tại A có $\hat{A} = 120^{\circ}$ . Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:

a) $Δ$ BAM = $Δ$ CAN;

b) Các tam giác ANB, AMC lần lượt cân tại N, M.

Phương pháp giải:

a) Chứng minh 2 tam giác bằng nhau theo trường hợp g-c-g

b) Chứng minh tam giác có 2 cạnh bằng nhau hoặc 2 góc bằng nhau

Lời giải:

a) Xét 2 tam giác vuông BAM và CAN có:

AB=AC(Do tam giác ABC cân tại A)

$\hat{B} = \hat{C}$ (Do tam giác ABC cân tại A)

=> $Δ B A M = Δ C A N$ (g.c.g)

Xét tam giác ABC cân tại A, có $\hat{A} = 120^{\circ}$ có:

$\hat{B} = \hat{C} = \frac{180^{o} - 120^{o}}{2} = 30^{o}$ .

Xét tam giác ABM vuông tại A có:

$\begin{array}{l} \hat{B} + \hat{B A M} + \hat{A M B} = 180^{o} \\ \Rightarrow 30^{o} + 90^{o} + \hat{A M B} = 180^{o} \\ \Rightarrow \hat{A M B} = 60^{o} \\ \Rightarrow \hat{A M C} = 180^{o} - \hat{A M B} = 180^{o} - 60^{o} = 120^{o} \end{array}$

Xét tam giác MAC có:

$\begin{array}{l} \hat{A M C} + \hat{M A C} + \hat{C} = 180^{o} \\ \Rightarrow 120^{o} + \hat{M A C} + 30^{o} = 180^{o} \\ \Rightarrow \hat{M A C} = 30^{o} = \hat{C} \end{array}$

$\Rightarrow$ Tam giác AMC cân tại M.

Vì $Δ B A M = Δ C A N$ =>BM=CN => BN=MC

Xét 2 tam giác ANB và AMC có:

AB=AC

$A N = A M$ (do $Δ B A M = Δ C A N$ )

BN=MC

=> $Δ A N B = Δ A M C$ (c.c.c)

Mà tam giác AMC cân tại M.

=> Tam giác ANB cân tại N.

Bài 4.39 trang 87 Toán lớp 7: Cho tam giác ABC vuông tại A có B = 60°. Trên cạnh BC lấy điểm M sao cho $\hat{C A M} = 30^{o}$ . Chứng minh rằng:

a) Tam giác CAM cân tại M;

b) Tam giác BAM là tam giác đều;

c) M là trung điểm của đoạn thẳng BC.

Phương pháp giải:

a) Dùng tính chất tổng 3 góc trong 1 tam giác bằng 180 độ suy ra góc A bằng góc C.

b) Chứng minh tam giác ABM cân có 1 góc bằng 60 độ

c) Dùng tính chất tổng 3 góc trong 1 tam giác bằng 180 độ để tính số đo 3 góc từ đó suy ra tam giác đều

Lời giải:

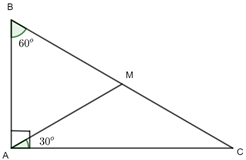
a) Xét tam giác ABC có:

$\begin{array}{l} \hat{A} + \hat{B} + \hat{C} = 180^{o} \\ => 90^{o} + 60^{o} + \hat{C} = 180^{o} \\ => \hat{C} = 30^{o} \end{array}$

Xét tam giác CAM có $\hat{A} = \hat{C} = 30^{o}$

=>Tam giác CAM cân tại M.

b) Xét tam giác ABM có:

$\begin{array}{l} \hat{C} + \hat{C M A} + \hat{C A M} = 180^{o} \\ => 30^{o} + \hat{C M A} + 30^{o} = 180^{o} \\ => \hat{C M A} = 120^{o} \\ => \hat{B M A} = 180^{o} - \hat{C M A} = 180^{o} - 120^{o} = 60^{o} \end{array}$