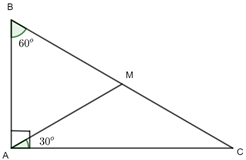
Bài 4.39 trang 87 Toán lớp 7: Cho tam giác ABC vuông tại A có B = 60°. Trên cạnh BC lấy điểm M sao cho $\widehat{CAM}={30}^o$. Chứng minh rằng:

a) Tam giác CAM cân tại M;

b) Tam giác BAM là tam giác đều;

c) M là trung điểm của đoạn thẳng BC.

Phương pháp giải:

Lời giải:

a)      Xét tam giác ABC có:

$\begin{array}{l}\hat{A}+\hat{B}+\hat{C}={180}^o\\ =>{90}^o+{60}^o+\hat{C}={180}^o\\ =>\hat{C}={30}^o\end{array}$

Xét tam giác CAM có $\hat{A}=\hat{C}={30}^o$

=>Tam giác CAM cân tại M.

b) Xét tam giác ABM có:

$\begin{array}{l}\hat{C}+\widehat{CMA}+\widehat{CAM}={180}^o\\ =>{30}^o+\widehat{CMA}+{30}^o={180}^o\\ =>\widehat{CMA}={120}^o\\ =>\widehat{BMA}={180}^o-\widehat{CMA}={180}^o-{120}^o={60}^o\end{array}$

Xét tam giác ABM có:

$\begin{array}{l}\hat{B}+\widehat{BMA}+\widehat{BAM}={180}^o\\ =>{60}^o+{60}^o+\widehat{BAM}={180}^o\\ =>\widehat{BAM}={60}^o\end{array}$

Do $\widehat{BAM}=\widehat{BMA}=\widehat{ABM}={60}^o$ nên tam giác ABM đều.

c) Do tam giác CAM cân tại M nên MA = MC (1).

Do tam giác BAM là tam giác đều nên MA = MB (2).

Từ (1) và (2) ta có MB = MC.

Mà M nằm giữa B và C nên M là trung điểm của BC.

Vậy M là trung điểm của BC.

Bài tập vận dụng:

Bài 1. Tính số đo x, y trong các hình dưới đây:

Hướng dẫn giải

a) Ta có: x + x + 30° + x + 15° = 180° (tổng ba góc trong tam giác)

⇒ 3x + 45° = 180°

⇒ 3x = 180° − 45°

⇒ 3x = 135°

⇒ x = 45°

Vậy x = 45°

b) Ta có: 3y – 10° = y + 60° (góc ngoài của tam giác)

⇒ 2y = 70°

⇒ y = 35°

Có: x + y + 60° = 180° (tổng ba góc trong tam giác)

⇒ x + 35° + 60° = 180°

⇒ x = 85°

Vậy x = 85°; y = 35°

Bài 2. Cho hình dưới đây, biết tam giác ABC vuông tại A, BD là tia phân giác của góc ABC và BA = BE. Chứng minh rằng:

a) <$\Delta ABD=\Delta EBD$ và $\widehat{BED}=90°$>;

b) BD là đường trung trực của cạnh AE;

c) Tam giác BFC là tam giác cân.

Hướng dẫn giải

a) Xét tam giác ABD và tam giác EBD có:

BA = BE (theo giả thiết)

$\widehat{ABD}=\widehat{EBD}$ (BD là tia phân giác của $\widehat{ABC}$)

BD là cạnh chung

Do đó, $\Delta ABD=\Delta EBD$ (c.g.c)

⇒ $\widehat{BAD}=\widehat{BED}$ (hai góc tương ứng)

Mà $\widehat{BAD}=90°$(theo giả thiết) ⇒ $\widehat{BED}=90°$ (đpcm)

b) Vì $\Delta ABD=\Delta EBD$ (chứng minh trên)

⇒ DA = DE (2 cạnh tương ứng)

⇒ D thuộc đường trung trực của AE (tính chất đường trung trực) (1)

Mà BA = BE (theo giả thiết)

⇒ B thuộc đường trung trực của AE (tính chất đường trung trực) (2)

Từ (1) và (2) ⇒ BD là đường trung trực của AE (đpcm)

c) Vì $\widehat{BED}=90°$ (chứng minh trên) ⇒ $\Delta EBF$ vuông tại E

Xét tam giác ABC (vuông tại A) và tam giác EBF (vuông tại E) có:

BA = BE (theo giả thiết)

$\widehat{ABC}$ là góc chung

⇒ $\Delta ABC=\Delta EBF$ (cạnh góc vuông – góc nhọn kề)

⇒ BC = BF (2 cạnh tương ứng)

⇒ $\Delta BFC$ cân tại B (đpcm).

Bài 3. Cho M, N là hai điểm phân biệt nằm trên đường trung trực của cạnh AB sao cho AM = BN. O là giao điểm của MN và AB. Chứng minh rằng:

a) $\Delta AMO=\Delta BNO$;

b) Tam giác AMN cân;

c) Nếu $\widehat{AMO}=30°$ thì tam giác AMB là tam giác đều.

Hướng dẫn giải

MN là đường trung trực của AB ⇒ MN ⊥ AB tại O và OA = OB

a) Xét hai tam giác vuông AMO và BNO có:

AM = BN (theo giả thiết)

OA = OB

⇒ $\Delta AMO=\Delta BNO$ (cạnh huyền – cạnh góc vuông)

b) Ta có: AN = BN (vì N thuộc đường trung trực của AB)

Mà AM = BN (theo giả thiết)

⇒ AN = AM

⇒ $\Delta AMN$ cân cân tại A (đpcm)

c) Tam giác AMO vuông tại O có:

$\widehat{AMO}+\widehat{MAO}=90°$ (hai góc phụ nhau)

⇒ $30°+\widehat{MAO}=90°$

⇒ $\widehat{MAO}=60°$ hay $\widehat{MAB}=60°$

Có: MA = MB (vì M thuộc đường trung trực của AB)

⇒ $\Delta AMB$ là tam giác cân

Mà $\widehat{MAB}=60°$

⇒ $\Delta AMB$ là tam giác đều (đpcm).