Hoạt động 5 trang 9, 10 Toán lớp 7: Giả sử hai điểm a, b lần lượt biểu diễn hai số nguyên a, b trên trục số nằm ngang. Với a < b, nêu nhận xét về vị trí của điểm a so với điểm b trên trục số đó.

Lời giải:

Hai điểm a, b lần lượt biểu diễn hai số nguyên a, b trên trục số nằm ngang.

Xét a < b.

+) Với a < 0, b < 0 và a < b.

Ta có hình vẽ minh họa như sau:

Khi đó, điểm a nằm bên trái điểm b.

+) Với a < 0, b > 0 và a < b.

Ta có hình vẽ minh họa như sau:

Khi đó, điểm a nằm bên trái điểm b.

+) Với a > 0, b > 0 và a < b.

Ta có hình vẽ minh họa như sau:

Khi đó, điểm a nằm bên trái điểm b.

Vậy với a < b thì điểm a nằm bên trái điểm b.

Lý thuyết So sánh các số hữu tỉ

4.1 So sánh hai số hữu tỉ

Trong hai số hữu tỉ khác nhau bao giờ cũng có một số nhỏ hơn số kia.

- Nếu số hữu tỉ a nhỏ hơn số hữu tỉ b thì ta viết a < b hay b > a

- Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương.

- Số hữu tỉ nhỏ hơn 0 gọi là số hữu tỉ âm.

- Số hữu tỉ 0 không là số hữu tỉ âm cũng không là số hữu tỉ dương

- Nếu a < b và  b < c thì a < c.

4.2 Cách so sánh hai số hữu tỉ

+ Khi hai số hữu tỉ cùng là phân số hoặc cùng là số thập phân, ta dùng quy tắc đã học ở lớp 6 để so sánh.

+ Các trường hợp khác hai trường hợp trên, để so sánh hai số hữu tỉ ta viết chúng cùng về dạng phân số (hoặc cùng dạng số thập phân) rồi so sánh chúng.

Ví dụ:

 a) So sánh $-\frac{1}{3}$ và $\frac{-2}{5}$

Hai phân số trên cùng là phân số, vì vậy ta sẽ áp dụng quy tắc so sánh hai phân số đã học.

Ta quy đồng để đưa hai phân số về cùng mẫu số dương

$-\frac{1}{3}=\frac{-1}{3}=\frac{(-1)\cdot 5}{3\cdot 5}=\frac{-5}{15}$;     $\frac{-2}{5}=\frac{(-2)\cdot 3}{5\cdot 3}=\frac{-6}{15}$     

Vì $-5>-6$ nên $\frac{-5}{15}>\frac{-6}{15}$. Suy ra $-\frac{1}{3}>\frac{-2}{5}$.

b) So sánh 1,206 và 1,3

Hai số trên cùng là số thập phân, vì vậy ta sẽ áp dụng quy tắc so sánh hai số thập phân.

Ta so sánh phần nguyên với nhau, khi phần nguyên bằng nhau ta sẽ so sánh đến phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn…

1,206 < 1,3 (vì phần nguyên bằng nhau, hàng phần mười có 2 < 3).

c) So sánh – 0,3 và $\frac{-2}{7}$

Ta thấy hai số trên chưa cùng là phân số hoặc số thập phân, vì vậy ta đưa chúng về cùng là phân số hoặc số thập phân sau đó so sánh chúng.

Ta có $-0,3=\frac{-3}{10}$, ta sẽ  áp dụng quy tắc so sánh hai phân số $\frac{-3}{10}$và $\frac{-2}{7}$

Ta có : $\frac{-3}{10}=\frac{(-3)\cdot 7}{10\cdot 7}=\frac{-21}{70}$;  $\frac{-2}{7}=\frac{(-2)\cdot 10}{7\cdot 10}=\frac{-20}{70}$   

Vì – 21 < –20 nên $\frac{-21}{70}<\frac{-20}{70}$. Suy ra – 0,3 < $\frac{-2}{7}$ .

4.3 Minh họa trên trục số

Hai điểm x, y lần lượt biểu diễn hai số hữu tỉ x, y trên trục số :

- Trên trục số nằm ngang: Nếu x < y hay y > x thì điểm x nằm bên trái điểm y.

- Trên trục số thẳng đứng: Nếu x < y hay y > x thì điểm x nằm phía dưới điểm y.

Ví dụ : So sánh hai số: – 2 và $\frac{-5}{3}$  

Ta có : $-2=\frac{-2}{1}=\frac{-6}{3}$ mà $\frac{-6}{3}<\frac{-5}{3}$ vậy nên $-2<\frac{-5}{3}$ .

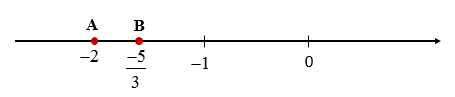Trên trục số nằm ngang điểm – 2 nằm bên trái điểm $\frac{-5}{3}$.

Xem thêm các giải bài giải Toán lớp 7 Cánh diều hay, chi tiết khác:

Câu hỏi khởi động trang 5 Toán lớp 7: Nhiệt độ lúc 13 giờ ngày 24/01/2016 tại một số trạm đo được bởi bảng như sau:...