Với tóm tắt lý thuyết Toán lớp 9 Bài 17: Vị trí tương đối của hai đường tròn sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Bài 17: Vị trí tương đối của hai đường tròn

A. Lý thuyết Vị trí tương đối của hai đường tròn

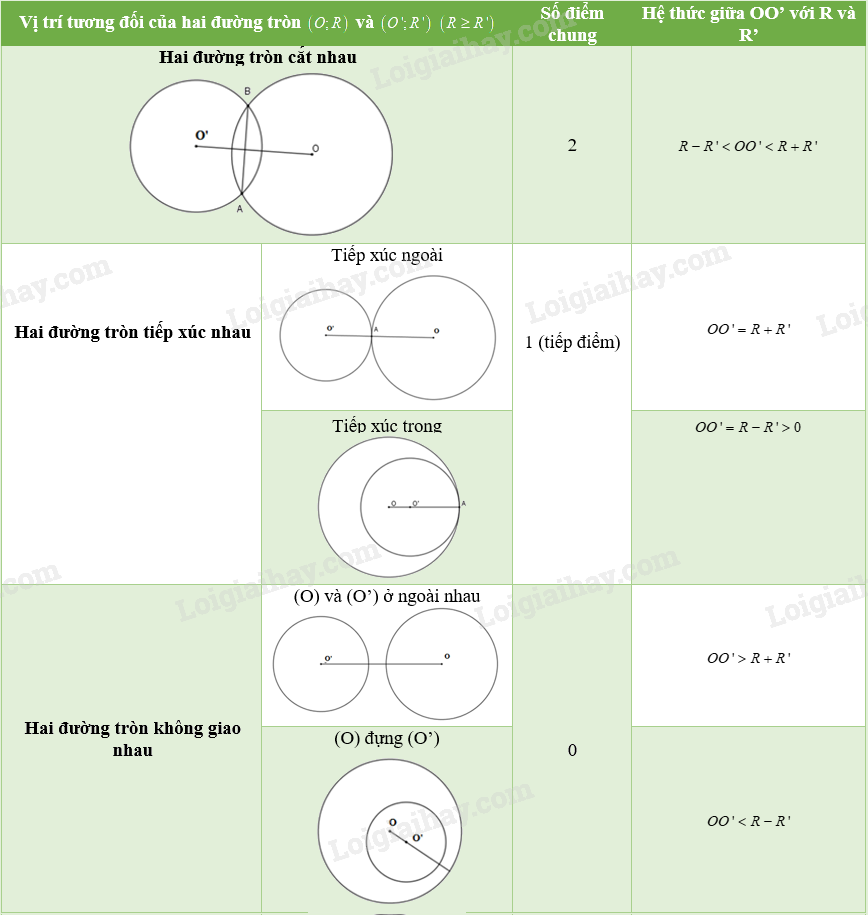
1. Hai đường tròn cắt nhau

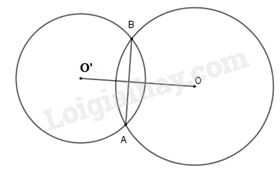
Hai đường tròn (O;R) và (O;R’) cắt nhau khi

$R-R^{\prime }<O{O}^{\prime }<R+R^{\prime }$ (với $R>R^{\prime }$)

Ví dụ: Cho OO’ = 5cm, khi đó hai đường tròn (O;4cm) và (O’;3cm) cắt nhau vì:

4cm – 3cm = 1cm < 5cm < 7cm = 4cm + 3cm.

2. Hai đường tròn tiếp xúc với nhau

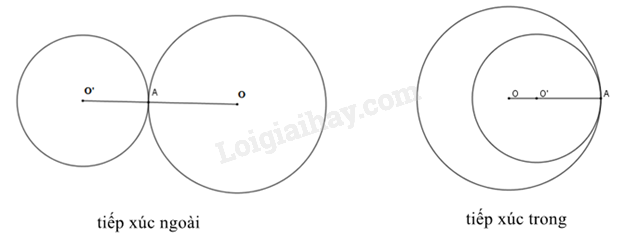
+ Hai đường tròn (O;R) và (O’;R’) tiếp xúc ngoài khi $O{O}^{\prime }=R+R^{\prime }$.

+ Hai đường tròn (O;R) và (O’;R’) tiếp xúc trong khi $O{O}^{\prime }=R-R^{\prime }\left(R>R^{\prime }\right)$.

Nếu hai đường tròn tiếp xúc với nhau thì tiếp điểm thẳng hàng với hai tâm.

Ví dụ:

Cho OO’ = 5cm, khi đó hai đường tròn (O;3cm) và (O’;2cm) tiếp xúc ngoài với nhau vì 5cm = 3cm + 2cm.

Cho OO’ = 3cm, khi đó hai đường tròn (O;8cm) và (O’;5cm) tiếp xúc trong với nhau vì 3cm = 8cm - 5cm.

3. Hai đường tròn không giao nhau

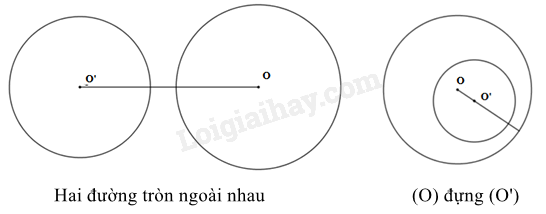
- Hai đường tròn (O;R) và (O’;R’) ngoài nhau khi $O{O}^{\prime }>R+R^{\prime }$;

- Đường tròn (O;R) đựng đường tròn (O’;R’) khi $R>R^{\prime }$ và $O{O}^{\prime }<R-R^{\prime }$.

Khi O trùng với O’ và $R\ne R^{\prime }$ thì ta có hai đường tròn đồng tâm.

Ví dụ: Cho đường tròn (O;3cm) và (O’;4cm) có $O{O}^{\prime }>8cm$ thì $O{O}^{\prime }=8cm>3cm+4cm=R+R^{\prime }$ nên (O;3cm) và (O’;4cm) là hai đường tròn ngoài nhau.

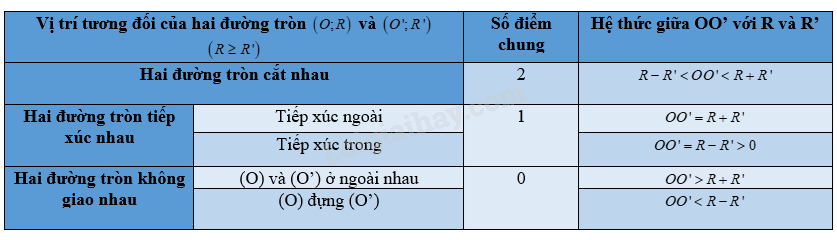
Bảng tổng kết vị trí tương đối của hai đường tròn

Sơ đồ tư duy Vị trí tương đối của hai đường tròn

B. Bài tập Vị trí tương đối của hai đường tròn

Bài 1. Nếu hai đường tròn không giao nhau thì số điểm chung của hai đường tròn là

A. 1;

B. 2;

C. 3;

D. 0.

Hướng dẫn giải

Đáp án đúng là: D

Nếu hai đường tròn không có điểm chung nào thì ta nói đó là hai đường tròn không giao nhau.

Vậy ta chọn phương án D.

Bài 2. Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Vẽ hai bán kính OM và O’N song song với nhau (M và N cùng nằm về một phía so với đường thẳng OO’). Tam giác MAN là tam giác gì?

A. Tam giác cân;

B. Tam giác vuông;

C. Tam giác đều;

D. Tam giác thường.

Hướng dẫn giải

Đáp án đúng là: B

Tam giác OAM cân tại O (do OM = OA) nên $\widehat{A_1}=\widehat{OMA}$.

Khi đó $\widehat{AOM}=180°-2\widehat{A_1}$         (1)

Tương tự, ta có $\widehat{A{O}^{\text{'}}N}=180°-2\widehat{A_2}$         (2)

Ta có OM // O’N, suy ra $\widehat{AOM}+\widehat{A{O}^{\text{'}}N}=180°$

Cộng (1) và (2) vế theo vế, ta được:

$\widehat{AOM}+\widehat{A{O}^{\text{'}}N}=360°-2\left(\widehat{A_1}+\widehat{A_2}\right)$

Suy ra $\widehat{A_1}+\widehat{A_2}=\frac{360°-\left(\widehat{AOM}+\widehat{A{O}^{\text{'}}N}\right)}{2}=\frac{360°-180°}{2}=90°.$

Ta có hai đường tròn (O) và (O’) tiếp xúc ngoài tại A nên A nằm trên đoạn thẳng OO’ hay ba điểm O, A, O’ thẳng hàng.

Khi đó: $\widehat{MAN}+\widehat{A_1}+\widehat{A_2}=180°$

Suy ra $\widehat{MAN}=180°-\left(\widehat{A_1}+\widehat{A_2}\right)=180°-90°=90°.$ .

Vậy tam giác MAN vuông tại A.

Bài 3. Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại A và B. Kẻ AC, AD lần lượt là đường kính của (O) và (O’). Biết OO’ = 13 cm, R = 12 cm, R’ = 5 cm. Cho các khẳng định sau:

(I) OA là tiếp tuyến của (O);

(II) OA là tiếp tuyến của (O’);

(III) Ba điểm C, B, D thẳng hàng.

Có bao nhiêu khẳng định đúng?

A. 0;

B. 1;

C. 2;

D. 3.

Hướng dẫn giải

Đáp án đúng là: D

⦁Ta có OA² + O’A² = R² + R’² = 12² + 5² = 169 và OO’² = 13² = 169.

Suy ra OA² + O’A² = OO’².

Áp dụng định lí Pythagore đảo, ta được tam giác OAO’ vuông tại A.

Khi đó OA ⊥ O’A tại A thuộc (O) và (O’).

Vì vậy OA là tiếp tuyến của (O) và OA cũng là tiếp tuyến của (O’).

Do đó (I), (II) đúng.

⦁Tam giác ABC, có $OB=\frac{AC}{2}\left(=OA\right)$ và O là trung điểm AC (do AC là đường kính của (O)) hay BO là đường truyến và có độ dài bằng nửa cạnh AC.

Suy ra tam giác ABC vuông tại B, nên AB ⊥ BC.

Chứng minh tương tự, ta được AB ⊥ BD.

Vì vậy ba điểm C, B, D thẳng hàng. Do đó (III) đúng.

Vậy cả 3 khẳng định đều đúng, ta chọn phương án D.

Bài 4.Xác định vị trí tương đối của hai đường tròn (O; R) và (O’; R’) trong mỗi trường hợp sau:

a) OO’ = 20; R = 8; R’ = 4.

b) OO’ = 15; R = 8; R’ = 7.

c) OO’ = 6; R = 9; R’ = 4.

d) OO’ = 0; R = 7; R’ = 5.

Hướng dẫn giải

a) Ta có 20 > 8 + 4 nên OO’ > R + R’, suy ra hai đường tròn (O; R) và (O’; R’) ở ngoài nhau.

b) Ta có 15 = 8 + 7 nên OO’ = R + R’, suy ra hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài.

c) Ta có 9 – 4 < 6 < 9 + 4 nên R – R’ < OO’ < R + R’, suy ra hai đường tròn (O; R) và (O’; R’) cắt nhau.

d) Ta có 0 < 7 – 5 nên 0 = OO’ < R – R’, suy ra đường tròn (O; R) và (O’; R’) đồng tâm và đường tròn (O; R) đựng đường tròn (O’; R’).

Bài 5. Cho hai đường tròn đồng tâm O, có bán kính lần lượt là R và r (R > r). Dây MN của đường tròn (O; R) cắt đường tròn (O; r) tại A và B. Gọi BC là đường kính của đường tròn (O; r). Tính giá trị của biểu thức AC² + AM² + AN² theo R và r.

Hướng dẫn giải

Kẻ OE ⊥ AB, OF ⊥ AC.

Ta có $OA=OB=OC=\frac{BC}{2}=r$

Suy ra tam giác ABC vuông tại A, nên AB ⊥ AC.

Ta có $\widehat{EAF}=\widehat{OEA}=\widehat{OFA}=90°$ nên tứ giác OEAF là hình chữ nhật.

Khi đó OF = AE và AF = OE.

Tam giác OAB cân tại O (do OA = OB) có OE là đường cao nên OE cũng là đường trung tuyến của tam giác OAB.

Do đó E là trung điểm AB hay AE = BE.

Chứng minh tương tự cho tam giác OMN, ta được E là trung điểm của MN nên ME = EN.

Suy ra ME – AE = EN – BE hay AM = BN.

Đặt AC = a, AM = b, AN = c.

Áp dụng định lí Pythagore cho tam giác OAE vuông tại E, ta được:

 $O{A}^2=O{E}^2+A{E}^2=A{F}^2+{\left(\frac{AB}{2}\right)}^2$       

$={\left(\frac{AC}{2}\right)}^2+{\left(\frac{AN-BN}{2}\right)}^2={\left(\frac{AC}{2}\right)}^2+{\left(\frac{AN-AM}{2}\right)}^2$

Do đó $r^2={\left(\frac{a}{2}\right)}^2+{\left(\frac{c-b}{2}\right)}^2$ .

Suy ra 4r² = a² + (c – b)²

Hay (2r)² = a² + c² + b² – 2bc      (1)

Áp dụng định lí Pythagore cho tam giác OEN vuông tại E, ta được:

$O{N}^2=O{E}^2+E{N}^2=A{F}^2+{\left(\frac{MN}{2}\right)}^2={\left(\frac{AC}{2}\right)}^2+{\left(\frac{AM+AN}{2}\right)}^2$.

Do đó $R^2={\left(\frac{a}{2}\right)}^2+{\left(\frac{b+c}{2}\right)}^2$ .

Suy ra 4R² = a² + (b + c)².

Hay (2R)² = a² + b² + c² + 2bc       (2)

Lấy (1) cộng (2) vế theo vế, ta được:

2(a² + b² + c²) = (2R)² + (2r)²

Suy ra $a^2+b^2+c^2=\frac{4\left(R^2+r^2\right)}{2}$

Hay AC² + AM² + AN² = 2(R² + r²).

Vậy AC² + AM² + AN² = 2(R² + r²).

Bài 6. Cho đường tròn (O; R) và một điểm A trên (O). Trên đoạn OA lấy điểm B sao cho $OB=\frac{1}{3}OA$.

a) Chứng minh đường tròn đường kính AB tiếp xúc với (O).

b) Đường tròn (O; R’) với R’ < R cắt đường tròn đường kính AB tại C. Tia AC cắt hai đường tròn đồng tâm tại D và E với D nằm giữa C và E. Chứng minh AC = CD = DE.

Hướng dẫn giải

a) Gọi I là trung điểm của AB.Suy ra I là tâm của đường tròn đường kính AB.

Ta có $OB=\frac{1}{3}OA$ hay $OA-AB=\frac{1}{3}OA$.

Do đó $AB=\frac{2}{3}OA$, nên AB < OA, suy ra IA < AB < OA.

Ta có OI = OA – IA > 0.

Vậy đường tròn đường kính AB tiếp xúc trong với (O).

b) Ta có  $AB=\frac{2}{3}OA$ (chứng minh trên)

Suy ra $IB=IA=\frac{AB}{2}=\frac{1}{3}OA$ (vì I là trung điểm AB)

Do đó IB = IA = OB.

Tam giác OAE cân tại O (do OA = OE = R), suy ra $\widehat{OEA}=\widehat{OAE}$       (1)

Chứng minh tương tự cho tam giác IAC, ta được $\widehat{ICA}=\widehat{IAC}$       (2)

Từ (1), (2), suy ra $\widehat{ICA}=\widehat{OEA}$.

Mà hai góc này ở vị trí đồng vị nên IC // OE.

Áp dụng định lí Thalès, ta được  $\frac{AC}{AE}=\frac{IA}{OA}=\frac{1}{3}$ hay $AC=\frac{1}{3}AE$      (3)

Kẻ OH vuông góc với DC.

Tam giác OCD cân tại O (OC = OD = R’) có OH là đường cao nên OH cũng là đường trung tuyến của tam giác OCD.

Do đó H là trung điểm CD,nên $HC=HD=\frac{CD}{2}$.

Tam giác ABC có: $IC=IB=IA=\frac{AB}{2}$ nên tam giác ABC vuông tại C, do đó BC ⊥ AE.

Mà OH ⊥ AE nên BC // OH.

Áp dụng định lí Thalès, ta được $\frac{AC}{AH}=\frac{AB}{AO}$.

Hay $\frac{AC}{AC+HC}=\frac{2}{3}$ , suy ra $\frac{AC+HC}{AC}=\frac{3}{2}$

Do đó $1+\frac{\frac{1}{2}\cdot CD}{AC}=\frac{3}{2}$  nên CD = AC. (4)

Từ (3), (4), ta suy ra  $CD=AC=\frac{1}{3}AE$   (5)

Ta có DE + CD + AC = AE.

Hay $DE+\frac{1}{3}AE+\frac{1}{3}AE=AE$ .

Suy ra $DE=\frac{1}{3}AE$      (6)

Từ (5), (6), ta suy ra AC = CD = DE.

Xem thêm các bài tóm tắt lý thuyết Toán lớp 9 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

Lý thuyết Bài 13: Mở đầu về đường tròn

Lý thuyết Bài 14: Cung và dây của một đường tròn

Lý thuyết Bài 15: Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên

Lý thuyết Bài 16: Vị trí tương đối của đường thẳng và đường tròn

Lý thuyết Bài 17: Vị trí tương đối của hai đường tròn