Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 9 Vị trí tương đối của hai đường tròn được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Vị trí tương đối của hai đường tròn. Mời các bạn đón xem:

Bài tập Toán 9 Vị trí tương đối của hai đường tròn

A. Bài tập Vị trí tương đối của hai đường tròn

Bài 1. Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Vẽ hai bán kính OM và O’N song song với nhau (M và N cùng nằm về một phía so với đường thẳng OO’). Tam giác MAN là tam giác gì?

A. Tam giác cân;

B. Tam giác vuông;

C. Tam giác đều;

D. Tam giác thường.

Hướng dẫn giải

Đáp án đúng là: B

Tam giác OAM cân tại O (do OM = OA) nên $\widehat{A_1}=\widehat{OMA}$.

Khi đó $\widehat{AOM}=180°-2\widehat{A_1}$         (1)

Tương tự, ta có $\widehat{A{O}^{\text{'}}N}=180°-2\widehat{A_2}$         (2)

Ta có OM // O’N, suy ra $\widehat{AOM}+\widehat{A{O}^{\text{'}}N}=180°$

Cộng (1) và (2) vế theo vế, ta được:

$\widehat{AOM}+\widehat{A{O}^{\text{'}}N}=360°-2\left(\widehat{A_1}+\widehat{A_2}\right)$

Suy ra $\widehat{A_1}+\widehat{A_2}=\frac{360°-\left(\widehat{AOM}+\widehat{A{O}^{\text{'}}N}\right)}{2}=\frac{360°-180°}{2}=90°.$

Ta có hai đường tròn (O) và (O’) tiếp xúc ngoài tại A nên A nằm trên đoạn thẳng OO’ hay ba điểm O, A, O’ thẳng hàng.

Khi đó: $\widehat{MAN}+\widehat{A_1}+\widehat{A_2}=180°$

Suy ra $\widehat{MAN}=180°-\left(\widehat{A_1}+\widehat{A_2}\right)=180°-90°=90°.$ .

Vậy tam giác MAN vuông tại A.

Bài 2. Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại A và B. Kẻ AC, AD lần lượt là đường kính của (O) và (O’). Biết OO’ = 13 cm, R = 12 cm, R’ = 5 cm. Cho các khẳng định sau:

(I) OA là tiếp tuyến của (O);

(II) OA là tiếp tuyến của (O’);

(III) Ba điểm C, B, D thẳng hàng.

Có bao nhiêu khẳng định đúng?

A. 0;

B. 1;

C. 2;

D. 3.

Hướng dẫn giải

Đáp án đúng là: D

⦁Ta có OA² + O’A² = R² + R’² = 12² + 5² = 169 và OO’² = 13² = 169.

Suy ra OA² + O’A² = OO’².

Áp dụng định lí Pythagore đảo, ta được tam giác OAO’ vuông tại A.

Khi đó OA ⊥ O’A tại A thuộc (O) và (O’).

Vì vậy OA là tiếp tuyến của (O) và OA cũng là tiếp tuyến của (O’).

Do đó (I), (II) đúng.

⦁Tam giác ABC, có $OB=\frac{AC}{2}\left(=OA\right)$ và O là trung điểm AC (do AC là đường kính của (O)) hay BO là đường truyến và có độ dài bằng nửa cạnh AC.

Suy ra tam giác ABC vuông tại B, nên AB ⊥ BC.

Chứng minh tương tự, ta được AB ⊥ BD.

Vì vậy ba điểm C, B, D thẳng hàng. Do đó (III) đúng.

Vậy cả 3 khẳng định đều đúng, ta chọn phương án D.

Bài 3. Cho hai đường tròn (O; 9 cm), (O’; 8 cm) với OO’ = 17 cm. Kết luận nào sau đây đúng về vị trí tương đối của hai đường tròn?

A. Hai đường tròn ở ngoài nhau;

B. Hai đường tròn tiếp xúc ngoài;

C. Hai đường tròn tiếp xúc trong;

D. Hai đường tròn cắt nhau.

Hướng dẫn giải

Đáp án đúng là: B

Ta thấy bán kính của hai đường tròn (O), (O’) lần lượt là R = 9 cm và r = 8 cm.

Vì R + r = 9 + 8 = 17 (cm) nên OO’ = R + r.

Vậy hai đường tròn đã cho tiếp xúc ngoài.

Bài 4. Xác định vị trí tương đối của hai đường tròn (O; R) và (O’; R’) trong mỗi trường hợp sau:

a) OO’ = 20; R = 8; R’ = 4.

b) OO’ = 15; R = 8; R’ = 7.

c) OO’ = 6; R = 9; R’ = 4.

d) OO’ = 1; R = 7; R’ = 5.

e) OO’ = 4; R = 6;R’ = 2.

Hướng dẫn giải

a) Ta thấy: R + R’ = 8 + 4 < 20 nên R + R’ < OO’.

Vậy hai đường tròn (O; R) và (O’; R’) ở ngoài nhau.

b) Ta thấy: R + R’ = 8 + 7 = 15 nên R + R’ = OO’.

Vậy hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài.

c) Ta thấy: 9 – 4 < 6 < 9 + 4 nên R – R’ < OO’ < R + R’.

Vậy hai đường tròn (O; R) và (O’; R’) cắt nhau.

d) Ta thấy: R – R’ = 7 – 5 > 1 nên R – R’ > OO’.

Vậy đường tròn (O; R) đựng đường tròn (O’; R’).

e) Ta thấy: R – R’ = 6 – 2 = 4 nên R – R’ = OO’.

Vậy hai đường tròn đã cho tiếp xúc trong với nhau.

Bài 5. Mô tả vị trí tương đối giữa mỗi cặp đường viền cồng chiêng trong hình chụp bộ cồng chiêng Tây Nguyên ở hình dưới đây.

Hướng dẫn giải

Cặp đường tròn mô tảđường viền ở cặp cồng chiêng trong Hình a) không có điểm chung nên cặp đường tròn này không giao nhau.

Cặp đường tròn mô tảđường viền ở cặp cồng chiêng trong Hình b) có một điểm chung và không có cồng chiêng nào treo trước cồng chiêng còn lại nên cặp đường tròn này tiếp xúc ngoài với nhau.

Cặp đường tròn mô tả đường viền ở cặp cồng chiêng trong Hình c) có hai điểm chung nên cặp đường tròn này cắt nhau tại hai điểm phân biệt.

B. Lý thuyết Vị trí tương đối của hai đường tròn

1. Hai đường tròn cắt nhau

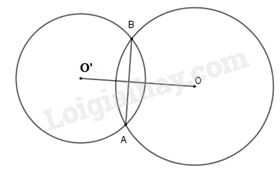
Hai đường tròn (O;R) và (O;R’) cắt nhau khi

$R-R^{\prime }<O{O}^{\prime }<R+R^{\prime }$ (với $R>R^{\prime }$)

Ví dụ: Cho OO’ = 5cm, khi đó hai đường tròn (O;4cm) và (O’;3cm) cắt nhau vì:

4cm – 3cm = 1cm < 5cm < 7cm = 4cm + 3cm.

2. Hai đường tròn tiếp xúc với nhau

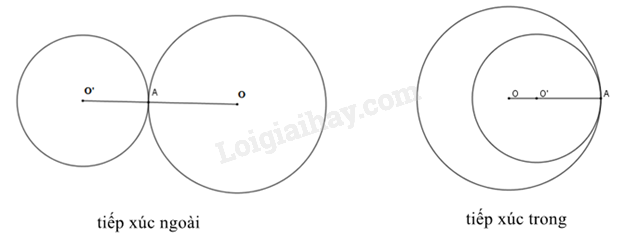
+ Hai đường tròn (O;R) và (O’;R’) tiếp xúc ngoài khi $O{O}^{\prime }=R+R^{\prime }$.

+ Hai đường tròn (O;R) và (O’;R’) tiếp xúc trong khi $O{O}^{\prime }=R-R^{\prime }\left(R>R^{\prime }\right)$.

Nếu hai đường tròn tiếp xúc với nhau thì tiếp điểm thẳng hàng với hai tâm.

Ví dụ:

Cho OO’ = 5cm, khi đó hai đường tròn (O;3cm) và (O’;2cm) tiếp xúc ngoài với nhau vì 5cm = 3cm + 2cm.

Cho OO’ = 3cm, khi đó hai đường tròn (O;8cm) và (O’;5cm) tiếp xúc trong với nhau vì 3cm = 8cm - 5cm.

3. Hai đường tròn không giao nhau

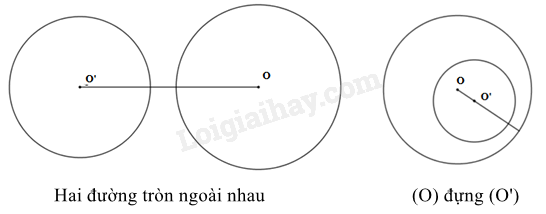
- Hai đường tròn (O;R) và (O’;R’) ngoài nhau khi $O{O}^{\prime }>R+R^{\prime }$;

- Đường tròn (O;R) đựng đường tròn (O’;R’) khi $R>R^{\prime }$ và $O{O}^{\prime }<R-R^{\prime }$.

Khi O trùng với O’ và $R\ne R^{\prime }$ thì ta có hai đường tròn đồng tâm.

Ví dụ: Cho đường tròn (O;3cm) và (O’;4cm) có $O{O}^{\prime }>8cm$ thì $O{O}^{\prime }=8cm>3cm+4cm=R+R^{\prime }$ nên (O;3cm) và (O’;4cm) là hai đường tròn ngoài nhau.

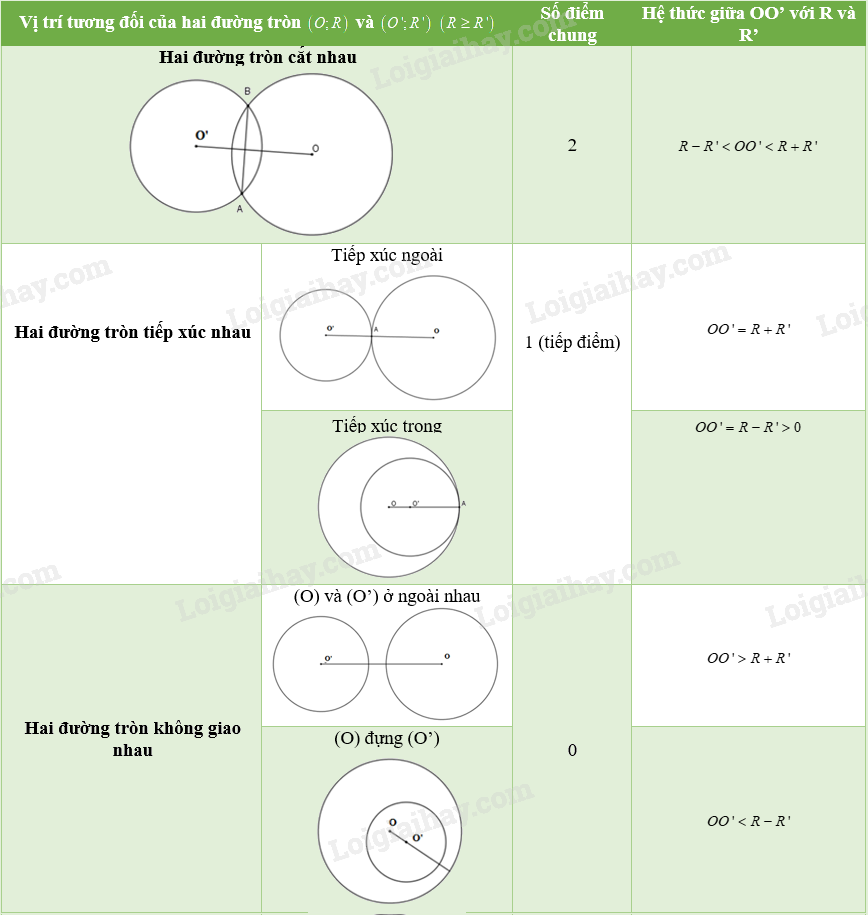
Bảng tổng kết vị trí tương đối của hai đường tròn

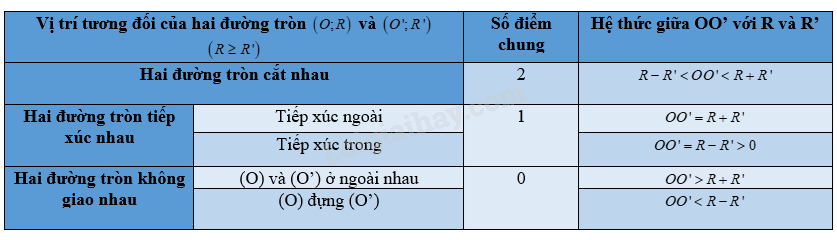
Sơ đồ tư duy Vị trí tương đối của hai đường tròn