Với giải sách bài tập Toán 9 Bài 17: Vị trí tương đối của hai đường tròn sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:

Giải SBT Toán 9 Bài 17: Vị trí tương đối của hai đường tròn

Bài 5.22 trang 68 sách bài tập Toán 9 Tập 1: Hai đường tròn (O; 2 cm) và (O'; 3 cm) có vị trí tương đối như thế nào trong mỗi trường hợp sau:

a) OO' = 4 cm?    

b) OO' = 5 cm?    

c) OO' = 6 cm?

Lời giải:

a) Do OO' = 4 < 5 = 2 + 3 nên (O) và (O') cắt nhau.

b) Do OO' = 5 = 2 + 3 nên (O) và (O') tiếp xúc với nhau.

c) Do OO' = 6 > 5 = 2 + 3 nên (O) và (O') không giao nhau.

Bài 5.23 trang 68 sách bài tập Toán 9 Tập 1: Vẽ hình và chứng minh phần b của Ví dụ 2.

Cho đường tròn (O) và dây AB không là đường kính của (O). Vị trí tương đối của (O) và (O'; O'C) sẽ như thế nào nếu O' thẳng hàng với O và A, nhưng nằm ngoài đoạn OA?

Lời giải:

TH1: OO' nằm cùng phía đối với A:

Do O'C // OB nên ∆OAB ᔕ ∆O'AC (g.g).

Mà OAB cân tại O nên O'AC cân tại O', suy ra O'A = O'C.

Do đó ta có OO' = O'A – OA = O'C – OA, suy ra (O'; O'C) tiếp xúc trong với (O; OA). (đpcm)

TH2: OO' nằm khác phía đối với A:

Do O'C // OB nên ∆OAB ᔕ ∆O'AC (g.g).

Mà OAB cân tại O nên O'AC cân tại O', suy ra O'A = O'C.

Suy ra OO' = O'A + OA = O'C + OA.

Do đó (O'; O'C) tiếp xúc ngoài với (O; OA). (đpcm)

Bài 5.24 trang 68 sách bài tập Toán 9 Tập 1: Cho điểm A và đường tròn (O; R) sao cho R < OA < 3R.

a) Chứng minh rằng đường tròn (A; 2R) cắt đường tròn (O; R). Gọi B là một trong hai giao điểm của chúng.

b) Gọi C là điểm đối xứng với B qua O. Nối A với C cắt (O) tại D (khác C). Chứng minh rằng AD = DC.

Lời giải:

a)  Theo đề bài, R < OA < 3R nên ta có:

R < OA < 3R

2R – R < OA < 2R + R

Suy ra hai đường tròn (A; 2R) và (O; R) cắt nhau.

b) Vì B nằm trên đường tròn (O; R) mà C đối xứng với B qua O nên BC là một đường kính của đường tròn (O; R).

Khi đó C nằm trên đường tròn (O; R) nên BC = 2R.

Vì B nằm trên đường tròn (A; 2R) nên AB là một bán kính của (A; 2R).

Suy ra AB = 2R.

Vì AB = BC = 2R nên tam giác ABC cân tại B.

Xét tam giác BCD có:

DO là trung tuyến (Do O là trung điểm BC)

$DO=R=\frac{BC}{2}$

Suy ra tam giác BCD vuông tại D, do đó BD ⊥ CD hay BD ⊥ AC.

BD ⊥ AC nên BD là đường cao của tam giác cân ABC, suy ra BD cũng đồng thời là đường trung tuyến của tam giác ABC hay D là trung điểm của AC.

Do đó AD = DC. (đpcm)

Bài 5.25 trang 68 sách bài tập Toán 9 Tập 1: Cho I là trung điểm của đoạn AB. Xét các đường tròn (I; IB) và (A; AB).

a) Hai đường tròn (I) và (A) nói trên có vị trí tương đối như thế nào?

b) Đường thẳng đi qua B, cắt các đường tròn (I) và (A) làn lượt tại C và D. Hãy so sánh các độ dài BC và CD.

Lời giải:

a) Vì I là trung điểm AB nên ta có AI = AB – IB.

Do đó hai đường tròn (I; IB) và (A; AB) tiếp xúc trong với nhau.

b) Vì D nằm trên đường tròn (A; AB) nên AD = AB, suy ra tam giác ACB cân tại A.

Xét tam giác ACB có:

CI là trung tuyến của tam giác (I là trung điểm AB)

$CI=IB=\frac{AB}{2}$ (CI là bán kính của (I), AB là đường kính của (I))

Suy ra tam giác ACB vuông tại C, do đó AC ⊥ CB hay AC ⊥ BD.

Tam giác ABD cân tại A có AC là đường cao nên AC đồng thời là đường trung tuyến của tam giác ABD, suy ra C là trung điểm BD hay CB = CD.

Vậy CB = CD.

Bài 5.26 trang 68 sách bài tập Toán 9 Tập 1: Cho tam giác ABC.

a) Chứng minh rằng hai đường tròn (B; BA) và (C; CA) cắt nhau. Gọi A' là giao điểm khác A của hai đường tròn đó.

b) Chứng minh rằng A và A' đối xứng nhau qua BC.

c) Biết rằng AA' = 24 cm, AB = 15 cm và AC = 13 cm. Tính độ dài BC.

Lời giải:

a) Áp dụng bất đẳng thức tam giác với tam giác ABC, ta có:

AB + AC > BC > AB – AC

Do đó tam giác (B; BA) và (C; CA) cắt nhau. (đpcm)

b) Xét ∆ABC và ∆A'BC có:

AB = A'B (A và A' cùng nằm trên đường tròn (B))

AC = A'C (A và A' cùng nằm trên đường tròn (C))

Chung cạnh BC

Do đó ∆ABC = ∆A'BC (c.c.c).

Suy ra $\widehat{ABC}=\widehat{A\text{'}BC}$(hai góc tương ứng) hay BC là đường phân giác của $\widehat{ABA\text{'}}.$

Mà tam giác ABA' cân tại B do AB = A'B, suy ra BC là đường phân giác của góc $\widehat{ABA\text{'}}.$ cũng đồng thời là đường trung trực của AA'.

Do đó A và A' đối xứng với nhau qua BC. (đpcm)

c) Gọi D là giao điểm của BC và AA'.

Theo câu b) ta có AD = DA' (do A và A' đối xứng qua BC) và BC ⊥ AA', suy ra tam giác ABD và ACD vuông tại D.

Do AD = A'D nên $AD=A\text{'}D=\frac{AA\text{'}}{2}=\frac{24}{2}=12$(cm).

+ Áp dụng định lý Pythagore với tam giác ABD, ta có:

$BD=\sqrt{A{B}^2-A{D}^2}=\sqrt{{15}^2-{12}^2}=9$ (cm)

+ Áp dụng định lý Pythagore với tam giác ADC ta có:

$DC=\sqrt{A{C}^2-A{D}^2}=\sqrt{{13}^2-{12}^2}=5$ (cm).

Vậy BC = BD + CD = 9 + 5 = 14 (cm).

Lý thuyết Vị trí tương đối của hai đường tròn

1. Hai đường tròn cắt nhau

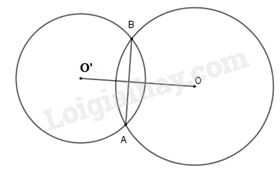
Hai đường tròn (O;R) và (O;R’) cắt nhau khi

$R-R^{\prime }<O{O}^{\prime }<R+R^{\prime }$ (với $R>R^{\prime }$)

Ví dụ: Cho OO’ = 5cm, khi đó hai đường tròn (O;4cm) và (O’;3cm) cắt nhau vì:

4cm – 3cm = 1cm < 5cm < 7cm = 4cm + 3cm.

2. Hai đường tròn tiếp xúc với nhau

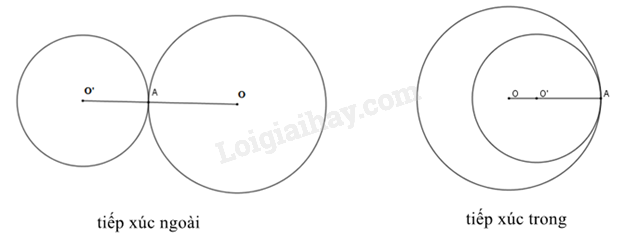
+ Hai đường tròn (O;R) và (O’;R’) tiếp xúc ngoài khi $O{O}^{\prime }=R+R^{\prime }$.

+ Hai đường tròn (O;R) và (O’;R’) tiếp xúc trong khi $O{O}^{\prime }=R-R^{\prime }\left(R>R^{\prime }\right)$.

Nếu hai đường tròn tiếp xúc với nhau thì tiếp điểm thẳng hàng với hai tâm.

Ví dụ:

Cho OO’ = 5cm, khi đó hai đường tròn (O;3cm) và (O’;2cm) tiếp xúc ngoài với nhau vì 5cm = 3cm + 2cm.

Cho OO’ = 3cm, khi đó hai đường tròn (O;8cm) và (O’;5cm) tiếp xúc trong với nhau vì 3cm = 8cm - 5cm.

3. Hai đường tròn không giao nhau

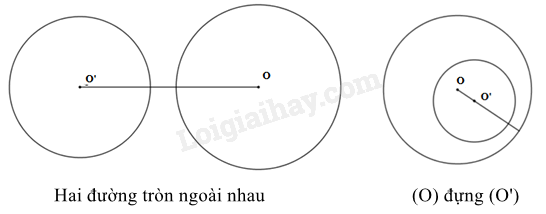
- Hai đường tròn (O;R) và (O’;R’) ngoài nhau khi $O{O}^{\prime }>R+R^{\prime }$;

- Đường tròn (O;R) đựng đường tròn (O’;R’) khi $R>R^{\prime }$ và $O{O}^{\prime }<R-R^{\prime }$.

Khi O trùng với O’ và $R\ne R^{\prime }$ thì ta có hai đường tròn đồng tâm.

Ví dụ: Cho đường tròn (O;3cm) và (O’;4cm) có $O{O}^{\prime }>8cm$ thì $O{O}^{\prime }=8cm>3cm+4cm=R+R^{\prime }$ nên (O;3cm) và (O’;4cm) là hai đường tròn ngoài nhau.

Bảng tổng kết vị trí tương đối của hai đường tròn

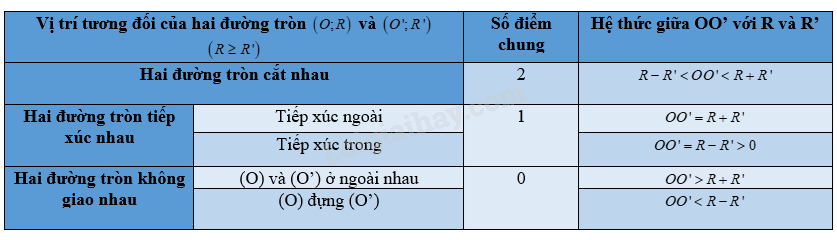
Xem thêm các bài giải SBT Toán lớp 9 Kết nối tri thức hay, chi tiết khác:

Bài 13: Mở đầu về đường tròn

Bài 14: Cung và dây của một đường tròn

Bài 15: Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên

Bài 16: Vị trí tương đối của đường thẳng và đường tròn

Bài 17: Vị trí tương đối của hai đường tròn

Bài tập cuối chương 5