Với tóm tắt lý thuyết Toán lớp 9 Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

A. Lý thuyết Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

1. Hệ thức giữa cạnh huyền và cạnh góc vuông

Công thức tính cạnh góc vuông theo cạnh huyền và sin, côsin của các góc nhọn

Ví dụ 1:

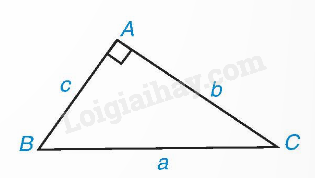
Trong tam giác ABC vuông tại A, ta có:

$\begin{array}{l}b=a.\sin B=a.\cos C;\\ c=a.\sin C=a.\cos B.\end{array}$

2. Hệ thức giữa hai cạnh góc vuông

Công thức tính cạnh góc vuông theo cạnh góc vuông kia và tang, côtang của các góc nhọn

Ví dụ 2:

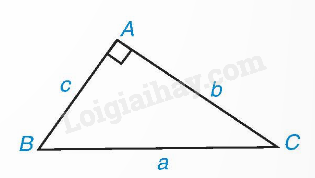
Trong tam giác ABC vuông tại A, ta có:

$\begin{array}{l}b=c.\tan B=c.\cot C;\\ c=b.\tan C=b.\cot B.\end{array}$

3. Giải tam giác vuông

Bài toán Giải tam giác vuông

Trong một tam giác vuông, nếu cho biết trước hai cạnh (hoặc một góc nhọn và một cạnh) thì ta sẽ tìm được tất cả các cạnh và các góc còn lại của tam giác vuông đó.

Sơ đồ tư duy Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

B. Bài tập Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

Bài 1. Giải tam giác ABC vuông tại A có BC = a, AC = b, AB = c, trong các trường hợp:

a) a = 22 cm, b = 16 cm;

b) b = 8 cm, $\hat{C}=45°$.

(Các kết quả làm tròn đến số thập phân thứ nhất hoặc làm tròn đến độ).

Hướng dẫn giải

a) Theo định lí Pythagore, ta có: a² = b² + c²

Suy ra c² = a² – b² = 22² – 16² = 228.

Do đó$c=\sqrt{228}=2\sqrt{57}\approx 15,1$ (cm).

Ta có:

• $\hat{A}=90°$ (do tam giác ABC vuông tại A).

• $\sin B=\frac{b}{a}=\frac{16}{22}\approx 0,72$, suy ra $\hat{B}\approx 46°$.

• Do $\hat{A}=90°$ nên $\hat{C}=\hat{A}-\hat{B}\approx 90°-46°=44°$.

Vậy c ≈ 15,1 cm; $\hat{A}=90°$; $\hat{B}\approx 46°$; $\hat{C}\approx 44°$.

b) Xét tam giác ABC vuông tại A, có $\hat{C}=45°$ suy ra $\hat{A}=90°$ $\hat{B}=45°.$

Suy ra, tam giác ABC là tam giác vuông cân (do $\hat{B}=\hat{C}=45°$).

Do đó, b = c = 8 (cm).

Theo định lí Pythagore, ta có: a² = b² + c² = 8² + 8² =128.

Do đó $a=\sqrt{128}=8\sqrt{2}\approx 11,31$ (cm).

Vậy a ≈ 11,31 cm; c = 8 cm; $\hat{A}=90°$, $\hat{B}=45°.$

Bài 2. Tìm các góc của hình thoi có hai đường chéo dài $\sqrt{3}$ và 3.

Hướng dẫn giải

Xét hình thoi ABCD, có AC ⊥ BD (tính chất hình thoi)

Ta có: $\tan \widehat{DBC}=\frac{3}{\sqrt{3}}=\sqrt{3}$, suy ra $\widehat{DBC}=60°$.

Mà $\widehat{DBC}=\frac{1}{2}\widehat{ABC}=120°$ nên $\hat{B}=\hat{D}=120°$ (tính chất hình thoi).

Ta có: AB // CD nên $\hat{B}+\hat{C}=180°$ (hai góc trong cùng phía)

Suy ra $\hat{C}=180°-120°=60°$

Do đó $\hat{A}=\hat{C}=60°$ (tính chất hình thoi).

Vậy $\hat{A}=\hat{C}=60°$; $\hat{B}=\hat{D}=120°$.

Bài 3. Một cây cao có chiều cao 6m. Để hái một buồng cau xuống, phải đặt thang tre sao cho đầu thang tre đạt độ cao đó, khi đó góc của thang tre với mặt đất là bao nhiêu, biết chiếc thang dài 8m.

Hướng dẫn giải

Theo đề bài, ta có hình vẽ sau:

Trong hình vẽ trên, BC là chiều dài của thang tre, AC là chiều cao của cây tre, và AB là khoảng cách từ thang tre tới cây tre.

Xét ∆ABC vuông tại A, ta có:

$\sin B=\frac{AC}{BC}=\frac{6}{8}=\frac{3}{4}$ ⇒ $\hat{B}\approx 48°$

Vậy góc giữa thang tre với mặt đất là 48°.

Xem thêm các bài tóm tắt lý thuyết Toán lớp 9 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 11: Tỉ số lượng giác của góc nhọn

Lý thuyết Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

Lý thuyết Bài 13: Mở đầu về đường tròn

Lý thuyết Bài 14: Cung và dây của một đường tròn

Lý thuyết Bài 15: Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên

Lý thuyết Bài 16: Vị trí tương đối của đường thẳng và đường tròn