Với tóm tắt lý thuyết Toán lớp 9 Bài 10: Căn bậc ba và căn thức bậc ba sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Bài 10: Căn bậc ba và căn thức bậc ba

A. Lý thuyết Căn bậc ba và căn thức bậc ba

1. Căn bậc ba

Khái niệm căn bậc ba của một số thực

Chú ý:

- Mỗi số a đều có duy nhất một căn bậc ba.

- Căn bậc ba của số a được kí hiệu là $\sqrt[3]{a}$, trong đó số 3 được gọi là chỉ số của căn.

Nhận xét: Từ định nghĩa căn bậc ba, ta có ${\left(\sqrt[3]{a}\right)}^3=\sqrt[3]{a^3}=a$ với mọi số thực a.

Ví dụ:

$\sqrt[3]{64}=\sqrt[3]{4^3}=4$;

$\sqrt[3]{-27}=\sqrt[3]{{\left(-3\right)}^3}=-3$.

Tính căn bậc ba của một số bằng máy tính cầm tay

Ta có thể sử dụng loại MTCT thích hợp để tính căn bậc ba của một số.

2. Căn thức bậc ba

Khái niệm căn thức bậc ba của một biểu thức

Chú ý:

- Căn thức bậc ba của biểu thức A được kí hiệu là $\sqrt[3]{A}$ , trong đó số 3 được gọi là chỉ số của căn.

Nhận xét: Từ định nghĩa căn bậc ba, ta có  ${\left(\sqrt[3]{A}\right)}^3 = \sqrt[3]{A^3} =A$

Tính căn bậc ba của một số bằng máy tính cầm tay

Để tính $\sqrt[3]{A}$ tại những giá trị cho trước của biến, ta thay các giá trị cho trước của biến vào căn thức rồi tính giá trị của biểu thức số nhận được. 

Sơ đồ tư duy Căn bậc ba và căn thức bậc ba

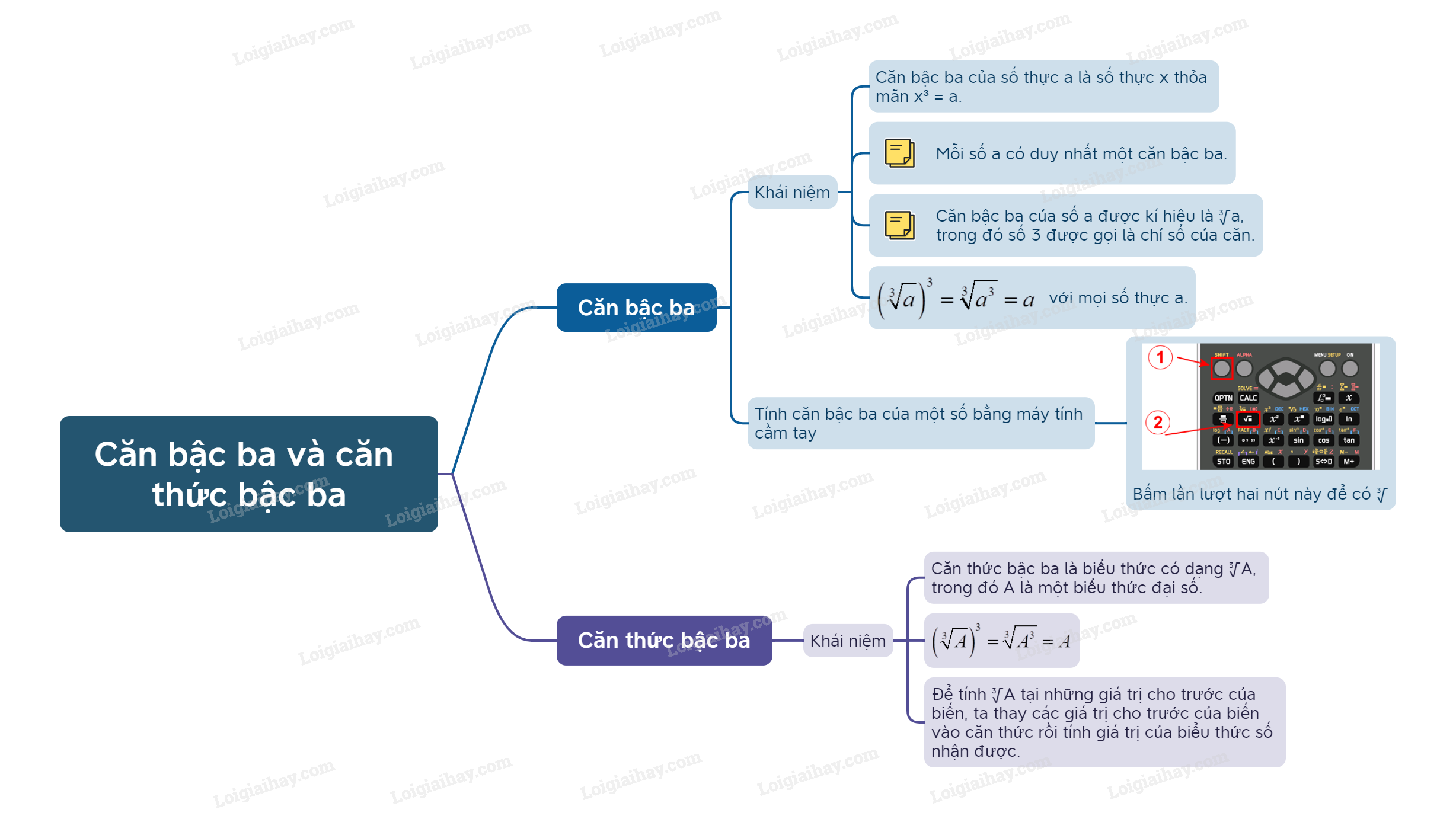
B. Bài tập Căn bậc ba và căn thức bậc ba

Bài 1. Tính:

a) $\sqrt[3]{343};$

b) $\sqrt[3]{-125};$

c) $\sqrt[3]{-0,008};$

d) $\sqrt[3]{0,729}.$

Hướng dẫn giải

a) Vì 7³ = 343 nên $\sqrt[3]{343}=7.$

b) Vì (−5)³ = −125 nên $\sqrt[3]{-125}=-5.$

c) Vì (−0,2)³ = −0,008 nên $\sqrt[3]{-0,008}=0,2.$

d) Vì 0,9³ = 0,729 nên $\sqrt[3]{0,729}=0,9.$

Bài 2. Một người thợ muốn làm một thùng tôn hình lập phương có thể tích bằng 1024 dm³. Bạn hãy ước lượng chiều dài cạnh thùng khoảng bao nhiêu dm?

Hướng dẫn giải

Công thức tính thể tích của một hình hộp chữ nhật có chiều dài cạnh a là V = a³, suy ra chiều dài cạnh là $a=\sqrt[3]{V}.$

Do đó, ta có chiều dài cạnh thùng tôn hình lập phương bằng:

$\sqrt[3]{1024}=\sqrt[3]{512.2}=\sqrt[3]{8^3.2}=8\sqrt{2}\approx 11,31$ (dm)

Vậy chiều dài cạnh thùng tôn khoảng 11,31 dm.

Bài 3. Rút gọn rồi tính giá trị của biểu thức $\sqrt[3]{8x^3-12x^2+6x-1}$ tại x = 5.

Hướng dẫn giải

Ta có: $\sqrt[3]{8x^3-12x^2+6x-1}$

$=\sqrt[3]{{\left(2x\right)}^3-3.{\left(2x\right)}^2.1+3.2x.1-1^3}$

$=\sqrt[3]{{\left(2x-1\right)}^3}$

$={\left(\sqrt[3]{2x-1}\right)}^3$

= 2x – 1

Tại x = 5, biểu thức có giá trị là 2.5 – 1 = 10 – 1 = 9.

Vậy tại x = 5, biểu thức $\sqrt[3]{8x^3-12x^2+6x-1}$ có giá trị là 9.

Bài 4. Rút gọn các biểu thức sau:

a) $\sqrt[3]{{\left(1-\sqrt{3}\right)}^3};$

b) $\sqrt[3]{{\left(3\sqrt{2}+1\right)}^3};$

c) ${\left(\sqrt[3]{\sqrt{5}+1}\right)}^3.$

Hướng dẫn giải

a) Ta có: $\sqrt[3]{{\left(1-\sqrt{3}\right)}^3}={\left(\sqrt[3]{1-\sqrt{3}}\right)}^3=1-\sqrt{3}.$

b) Ta có: $\sqrt[3]{{\left(3\sqrt{2}+1\right)}^3}={\left(\sqrt[3]{3\sqrt{2}+1}\right)}^3=3\sqrt{2}+1.$

c) Ta có: ${\left(\sqrt[3]{\sqrt{5}+1}\right)}^3=\sqrt{5}+1.$

Xem thêm các bài tóm tắt lý thuyết Toán lớp 9 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 9: Biến đổi đơn giản và rút gọn biểu thức chứa căn thức bậc hai

Lý thuyết Bài 10: Căn bậc ba và căn thức bậc ba

Lý thuyết Bài 11: Tỉ số lượng giác của góc nhọn

Lý thuyết Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

Lý thuyết Bài 13: Mở đầu về đường tròn

Lý thuyết Bài 14: Cung và dây của một đường tròn