Lý thuyết Biến đổi đơn giản và rút gọn biểu thức chứa căn thức bậc hai (Kết nối tri thức 2024)

Lý thuyết Biến đổi đơn giản và rút gọn biểu thức chứa căn thức bậc hai (Kết nối tri thức 2024) | Lý thuyết Toán 9

Nguyễn Mạnh Tài Ngày: 08-08-2024 Lớp 9

595

Với tóm tắt lý thuyết Toán lớp 9 Bài 9: Biến đổi đơn giản và rút gọn biểu thức chứa căn thức bậc hai sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Bài 9: Biến đổi đơn giản và rút gọn biểu thức chứa căn thức bậc hai

A. Lý thuyết Biến đổi đơn giản và rút gọn biểu thức chứa căn thức bậc hai

1. Đưa thừa số ra ngoài dấu căn

Phép đưa thừa số ra ngoài dấu căn

Nếu a là một số và b là một số không âm thì $\sqrt{a^{2} . b} = | a | \sqrt{b}$ .

Ví dụ:

$\sqrt{45} = \sqrt{3^{2} .5} = 3 \sqrt{5}$ ;

$\sqrt{243 a} = \sqrt{9^{2} .3 a} = 9 \sqrt{3 a}$ .

Với những căn thức bậc hai mà biểu thức dưới dấu căn có mẫu, ta thường khử mẫu của biểu thức lấy căn (biến đổi căn thức bậc hai đó thành một biểu thức mà trong căn thức không còn mẫu).

Ví dụ: $\sqrt{\frac{4}{7}} = \sqrt{\frac{4.7}{7^{2}}} = \sqrt{{(\frac{2}{7})}^{2} .7} = \frac{2 \sqrt{7}}{7}$ .

2. Đưa thừa số vào trong dấu căn

Phép đưa thừa số vào trong dấu căn

- Nếu a và b là hai số không âm thì $a \sqrt{b} = \sqrt{a^{2} b}$ .

- Nếu a là số âm và b là số không âm thì $a \sqrt{b} = - \sqrt{a^{2} b}$ .

Ví dụ:

$5 \sqrt{2} = \sqrt{5^{2} .2} = \sqrt{50}$ ;

Với $a \geq 0$ thì $- 2 \sqrt{a} = - \sqrt{2^{2} . a} = - \sqrt{4 a}$ .

3. Trục căn thức ở mẫu

Cách trục căn thức ở mẫu

- Với các biểu thức A, B và B > 0, ta có $\frac{A}{\sqrt{B}} = \frac{A \sqrt{B}}{B}$ .

- Với các biểu thức A, B, C mà $A \geq 0, A \neq B^{2}$ , ta có:

$\frac{C}{\sqrt{A} + B} = \frac{C (\sqrt{A} - B)}{A - B^{2}}; \frac{C}{\sqrt{A} - B} = \frac{C (\sqrt{A} + B)}{A - B^{2}}$ .

- Với các biểu thức A, B, C mà $A \geq 0, B \geq 0, A \neq B$ , ta có:

$\frac{C}{\sqrt{A} + \sqrt{B}} = \frac{C (\sqrt{A} - \sqrt{B})}{A - B}; \frac{C}{\sqrt{A} - \sqrt{B}} = \frac{C (\sqrt{A} + \sqrt{B})}{A - B}$ .

Ví dụ:

$\frac{2}{3 \sqrt{5}} = \frac{2 \sqrt{5}}{3 {(\sqrt{5})}^{2}} = \frac{2 \sqrt{5}}{3.5} = \frac{2 \sqrt{5}}{15}$ ;

$\frac{a}{3 - 2 \sqrt{2}} = \frac{a (3 + 2 \sqrt{2})}{(3 - 2 \sqrt{2}) . (3 + 2 \sqrt{2})} = \frac{a (3 + 2 \sqrt{2})}{3^{2} - {(2 \sqrt{2})}^{2}} = \frac{a (3 + 2 \sqrt{2})}{9 - 8} = (3 + 2 \sqrt{2}) a$ .

4. Rút gọn biểu thức chứa căn thức bậc hai

Khi rút gọn biểu thức có chứa căn thức bậc hai, ta cần phối hợp các phép tính (cộng, trừ, nhân, chia) và các phép biến đổi đã học (đưa thừa số ra ngoài hoặc vào trong dấu căn; khử mẩu của biểu thức lấy căn; trục căn thức ở mẫu).

Ví dụ:

$\begin{array}{l} A = 2 \sqrt{3} - \sqrt{75} + \sqrt{{(1 - \sqrt{3})}^{2}} \\ = 2 \sqrt{3} - \sqrt{{3.5}^{2}} + | 1 - \sqrt{3} | \\ = 2 \sqrt{3} - 5 \sqrt{3} + \sqrt{3} - 1 \\ = - 1 - 2 \sqrt{3} \end{array}$

$\begin{array}{l} B = x \sqrt{x} - \frac{x^{2} - x}{\sqrt{x} + 1} \\ = x \sqrt{x} - \frac{(x^{2} - x) (\sqrt{x} - 1)}{(\sqrt{x} + 1) (\sqrt{x} - 1)} \\ = x \sqrt{x} - \frac{x (x - 1) (\sqrt{x} - 1)}{(\sqrt{x} + 1) (\sqrt{x} - 1)} \\ = x \sqrt{x} - \frac{x (x - 1) (\sqrt{x} - 1)}{x - 1} \\ = x \sqrt{x} - x (\sqrt{x} - 1) \\ = x \sqrt{x} - x \sqrt{x} + x \\ = x \end{array}$

Sơ đồ tư duy Biến đổi đơn giản và rút gọn biểu thức chứa căn thức bậc hai

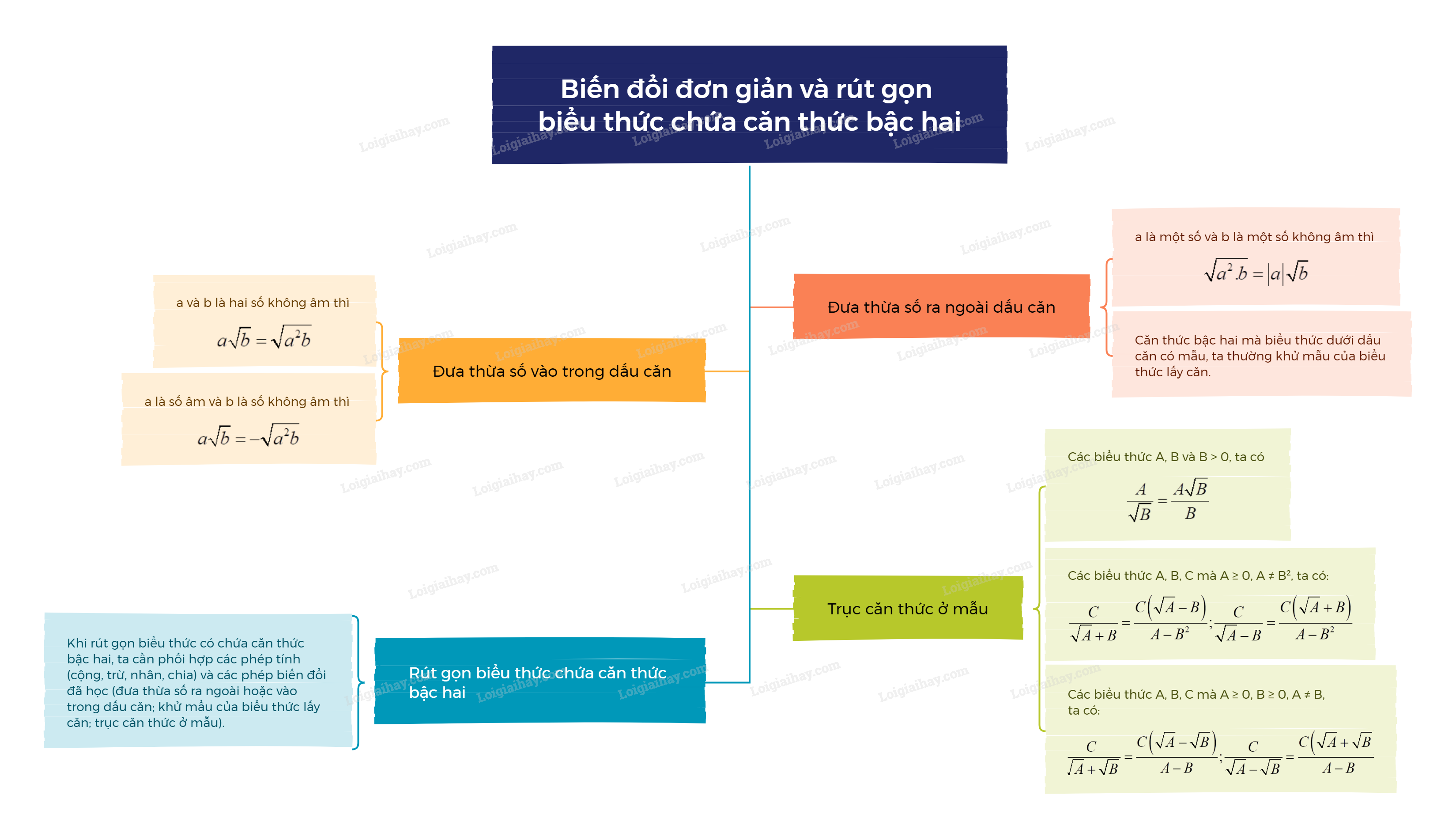
B. Bài tập Biến đổi đơn giản và rút gọn biểu thức chứa căn thức bậc hai

Bài 1. Đưa thừa số ra ngoài dấu căn:

a) $\sqrt{48};$

b) $\sqrt{72 a}$ (a ≥ 0);

c) $\sqrt{4 \sqrt{7} - 8};$

d) $\sqrt{50 \sqrt{3} + 100} .$

Hướng dẫn giải

a) Ta có: 48 = 4².3 nên $\sqrt{48} = \sqrt{4^{2} .3} = 4 \sqrt{3} .$

b) Ta có: 72 = 6².2 nên $\sqrt{72 a} = \sqrt{6^{2} .2 a} = 6 \sqrt{2 a} .$

c) Ta có: $\sqrt{4 \sqrt{7} - 8} = \sqrt{4 (\sqrt{7} - 2)}$

$= \sqrt{2^{2} (\sqrt{7} - 2)} = 2 \sqrt{\sqrt{7} - 2} .$

d) Ta có: $\sqrt{50 \sqrt{3} + 100} = \sqrt{50 (\sqrt{3} + 2)}$

$= \sqrt{5^{2} .2 (\sqrt{3} + 2)} = 5 \sqrt{2 \sqrt{3} + 4} .$

Bài 2. Đưa thừa số vào trong dấu căn:

a) $7 \sqrt{2};$

b) $- 3 \sqrt{5};$

c) $3 \sqrt{\frac{13}{9}};$

d) $- 4 \sqrt{\frac{13}{4} .}$

Hướng dẫn giải

a) Ta có: $7 \sqrt{2} = \sqrt{7^{2} .2} = \sqrt{49.2} = \sqrt{98} .$

b) Ta có: $- 3 \sqrt{5} = - \sqrt{3^{2} .5} = - \sqrt{9.5} = - \sqrt{45} .$

c) Ta có: $3 \sqrt{\frac{13}{9}} = \sqrt{3^{2} . \frac{13}{9}} = \sqrt{9. \frac{13}{9}} = \sqrt{13} .$

d) Ta có: $- 4 \sqrt{\frac{13}{4}} = - \sqrt{4^{2} . \frac{13}{4}} = - \sqrt{13.4} = - \sqrt{52} .$

Bài 3. Trục căn thức ở mẫu:

a) $\frac{7 + 2 \sqrt{3}}{\sqrt{3}};$

b) $\frac{1}{\sqrt{6} - 3};$

c) $\frac{5 + \sqrt{5}}{1 - \sqrt{5}};$

d) $\frac{\sqrt{8}}{\sqrt{2} + \sqrt{3}} .$

Hướng dẫn giải

a) Nhân cả tử và mẫu của biểu thức đã cho với $\sqrt{3},$ ta được:

$\frac{7 + 2 \sqrt{3}}{\sqrt{3}} = \frac{7 \sqrt{3} + 2.3}{3} = \frac{7 \sqrt{3} + 6}{3} .$

b) Biểu thức liên hợp của mẫu là $\sqrt{6} + 3.$ Nhân cả tử và mẫu của biểu thức đã cho với $\sqrt{6} + 3,$ ta được:

$\frac{1}{\sqrt{6} - 3} = \frac{\sqrt{6} + 3}{(\sqrt{6} - 3) (\sqrt{6} + 3)} = \frac{\sqrt{6} + 3}{6 - 9} = - \frac{\sqrt{6} + 3}{3} .$

c) Biểu thức liên hợp của mẫu là $1 + \sqrt{5} .$ Nhân cả tử và mẫu của biểu thức đã cho với $1 + \sqrt{5},$ ta được:

$\frac{5 + \sqrt{5}}{1 - \sqrt{5}} = \frac{\sqrt{5} {(1 + \sqrt{5})}^{2}}{(1 - \sqrt{5}) (1 + \sqrt{5})} = \frac{\sqrt{5} (6 + 2 \sqrt{5})}{1 - 5} = - \frac{6 \sqrt{5} + 10}{4} = - \frac{3 \sqrt{5} + 5}{2} .$

d) Biểu thức liên hợp của mẫu là $\sqrt{2} - \sqrt{3} .$ Nhân cả tử và mẫu của biểu thức đã cho với $\sqrt{2} - \sqrt{3},$ ta được:

$\frac{\sqrt{8}}{\sqrt{2} + \sqrt{3}} = \frac{\sqrt{8} (\sqrt{2} - \sqrt{3})}{(\sqrt{2} + \sqrt{3}) (\sqrt{2} - \sqrt{3})} = \frac{\sqrt{16} - \sqrt{24}}{2 - 3} = 2 \sqrt{6} - 4.$