Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 9 Căn bậc ba và căn thức bậc ba được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 9. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Căn bậc ba và căn thức bậc ba. Mời các bạn đón xem:

Bài tập Toán 9 Căn bậc ba và căn thức bậc ba

A. Bài tập Căn bậc ba và căn thức bậc ba

Bài 1. Một người thợ muốn làm một thùng tôn hình lập phương có thể tích bằng 1024 dm³. Bạn hãy ước lượng chiều dài cạnh thùng khoảng bao nhiêu dm?

Hướng dẫn giải

Công thức tính thể tích của một hình hộp chữ nhật có chiều dài cạnh a là V = a³, suy ra chiều dài cạnh là $a=\sqrt[3]{V}.$

Do đó, ta có chiều dài cạnh thùng tôn hình lập phương bằng:

$\sqrt[3]{1024}=\sqrt[3]{512.2}=\sqrt[3]{8^3.2}=8\sqrt{2}\approx 11,31$ (dm)

Vậy chiều dài cạnh thùng tôn khoảng 11,31 dm.

Bài 2. Rút gọn rồi tính giá trị của biểu thức $\sqrt[3]{8x^3-12x^2+6x-1}$ tại x = 5.

Hướng dẫn giải

Ta có: $\sqrt[3]{8x^3-12x^2+6x-1}$

$=\sqrt[3]{{\left(2x\right)}^3-3.{\left(2x\right)}^2.1+3.2x.1-1^3}$

$=\sqrt[3]{{\left(2x-1\right)}^3}$

$={\left(\sqrt[3]{2x-1}\right)}^3$

= 2x – 1

Tại x = 5, biểu thức có giá trị là 2.5 – 1 = 10 – 1 = 9.

Vậy tại x = 5, biểu thức $\sqrt[3]{8x^3-12x^2+6x-1}$ có giá trị là 9.

Bài 3. Tìm căn bậc ba của mỗi số sau:

a) −125;

b) 216;

c) $2\frac{10}{27}.$

Hướng dẫn giải

a) Ta có (−5)³ = −125, suy ra $\sqrt[3]{-125}=-5.$

b) Ta có 6³ = 216, suy ra $\sqrt[3]{216}=6.$

c) Ta có $2\frac{10}{27}=\frac{64}{27}$ mà ${\left(\frac{4}{3}\right)}^3=\frac{64}{27}.$ Suy ra $\sqrt[3]{2\frac{10}{27}}=\frac{4}{3}.$

Bài 4. Tìm x, biết:

a) x³ = 0,027;

b) $\sqrt[3]{x}=4;$

c) $\sqrt[3]{x}=0,7.$

Hướng dẫn giải

a) Ta có 0,3³ = 0,027, suy ra x = 0,3.

b) Ta có 4³ = 64 suy ra $x={\left(\sqrt[3]{x}\right)}^3=4^3=64.$

c) Ta có (0,7)³ = 0,343 suy ra $x={\left(\sqrt[3]{x}\right)}^3=0,7^3=0,343.$

Bài 5.Công thức $h=0,4\sqrt[3]{x}$ biểu diễn mối tương quan giữa cân nặng x (tính bằng kg) và chiều cao h (tính bằng m) của một con hươu cao cổ.

a) Một con hươu cao cổ cân nặng 195 kg thì cao bao nhiêu mét? (làm tròn kết quả đến hàng phần trăm).

b) Một con hươu cao cổ có chiều cao 2,62 m thì cân nặng bao nhiêu kilôgam? (làm tròn kết quả đến hàng đơn vị).

Hướng dẫn giải

a) Con hươu cao cổ nặng 195 kg thì x = 195.

Thay x = 195 vào công thức $h=0,4\sqrt[3]{x}$ ta được chiều cao của con hươu cao cổ là:

$h=0,4\sqrt[3]{x}=0,4\sqrt[3]{195}\approx 2,32$ (m).

b) Con hươu cao cổ cao 2,62 m thì h = 2,62.

Thay h = 2,62vào công thức $h=0,4\sqrt[3]{x}$ ta được phương trình:

$2,62=0,4\sqrt[3]{x}.$

Giải phương trình:

$2,62=0,4\sqrt[3]{x}.$

$\sqrt[3]{x}=6,55$

x ≈ 281 (kg).

Vậy con hươu cao cổ có chiều cao 2,62 m thì cân nặng khoảng 281kg.

B. Lý thuyết Căn bậc ba và căn thức bậc ba

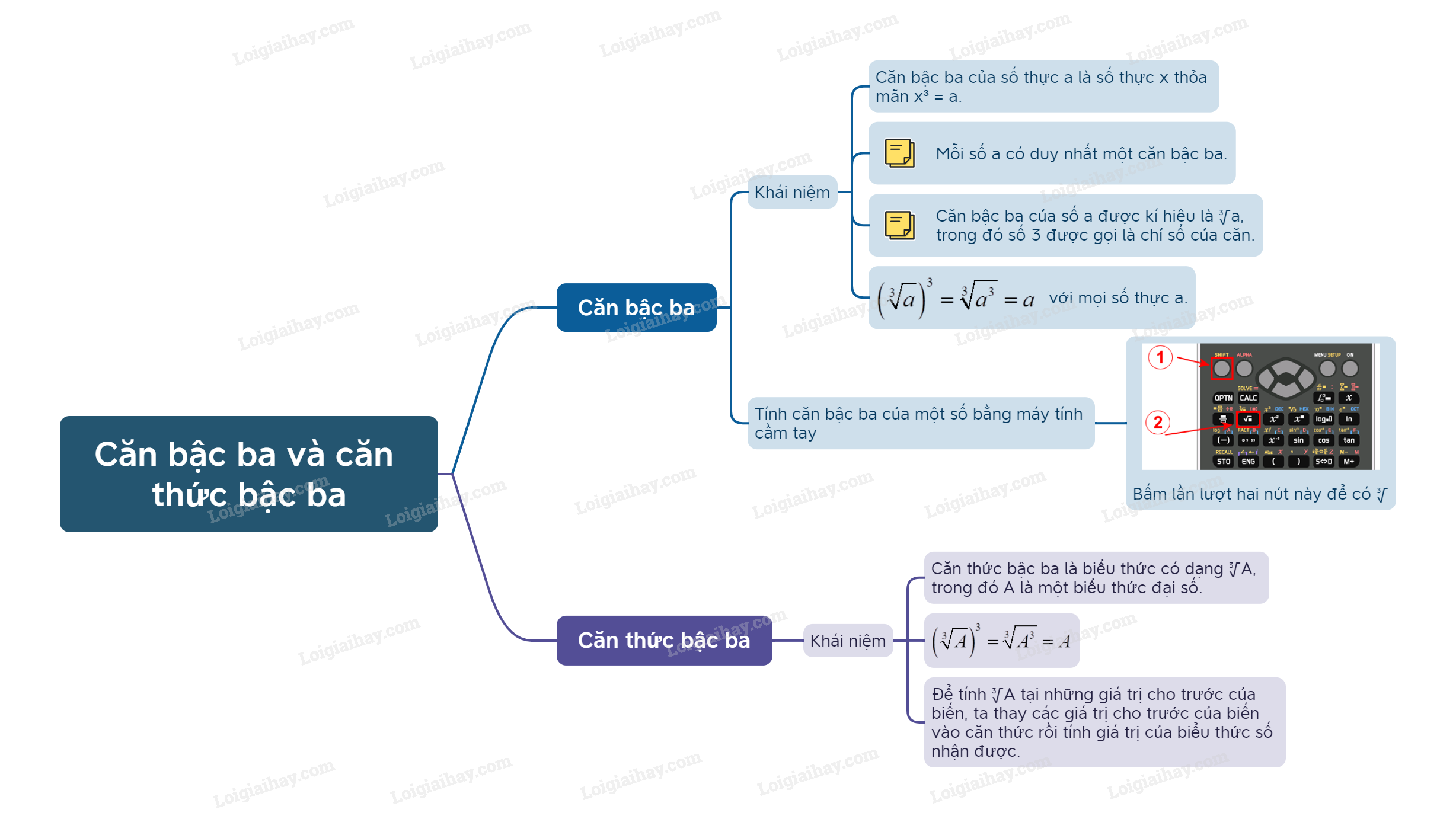
1. Căn bậc ba

Khái niệm căn bậc ba của một số thực

Chú ý:

- Mỗi số a đều có duy nhất một căn bậc ba.

- Căn bậc ba của số a được kí hiệu là $\sqrt[3]{a}$, trong đó số 3 được gọi là chỉ số của căn.

Nhận xét: Từ định nghĩa căn bậc ba, ta có ${\left(\sqrt[3]{a}\right)}^3=\sqrt[3]{a^3}=a$ với mọi số thực a.

Ví dụ:

$\sqrt[3]{64}=\sqrt[3]{4^3}=4$;

$\sqrt[3]{-27}=\sqrt[3]{{\left(-3\right)}^3}=-3$.

Tính căn bậc ba của một số bằng máy tính cầm tay

Ta có thể sử dụng loại MTCT thích hợp để tính căn bậc ba của một số.

2. Căn thức bậc ba

Khái niệm căn thức bậc ba của một biểu thức

Chú ý:

- Căn thức bậc ba của biểu thức A được kí hiệu là $\sqrt[3]{A}$ , trong đó số 3 được gọi là chỉ số của căn.

Nhận xét: Từ định nghĩa căn bậc ba, ta có  ${\left(\sqrt[3]{A}\right)}^3 = \sqrt[3]{A^3} =A$

Tính căn bậc ba của một số bằng máy tính cầm tay

Để tính $\sqrt[3]{A}$ tại những giá trị cho trước của biến, ta thay các giá trị cho trước của biến vào căn thức rồi tính giá trị của biểu thức số nhận được. 

Sơ đồ tư duy Căn bậc ba và căn thức bậc ba