Với giải Bài 3.24 trang 57 Toán lớp 7 Kết nối tri thức với cuộc sống chi tiết trong Bài 11: Định lí và chứng minh định lí giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 7. Mời các bạn đón xem:
Giải bài tập Toán lớp 7 Bài 11: Định lí và chứng minh định lí
Bài 3.24 trang 57 Toán lớp 7: Có thể coi định lí: “Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” được suy ra trực tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song không? Suy ra như thế nào?
Phương pháp giải:
Lời giải:
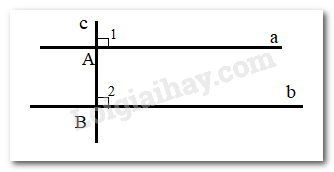
Giả sử có 2 đường thẳng phân biệt a,b cùng vuông góc với một đường thẳng c.
Ta có: , mà hai góc này ở vị trí đồng vị nên a//b (Dấu hiệu nhận biết 2 đường thẳng song song)
Như vậy, định lí trên có thể được suy ra trực tiếp từ định lí về dấu hiệu nhận biết hai đường thẳng song song.
Bài tập vận dụng:
Bài 1. Vẽ hình, viết giả thiết, kết luận và chứng minh định lí: “Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông”.
Hướng dẫn giải
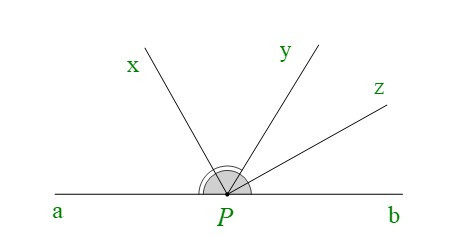
|
GT |
và là hai góc kề bù Px là tia phân giác của Pz là tia phân giác của |
|
KL |
là góc vuông |
Vì Px là tia phân giác của nên
Vì Pz là tia phân giác của nên
Nên
Mà ta có: + = 180° (hai góc kề bù)
Do đó:
Mặt khác:
Vậy , tức là là góc vuông.
Bài 2. Cho hình vẽ dưới đây. Biết Ax song song với Cy.
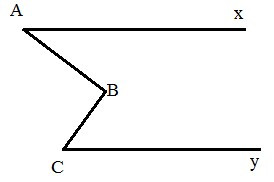
Chứng minh rằng
Hướng dẫn giải
|
GT |
|
|
KL |
|
Qua B, kẻ đường thẳng mn song song với đường thẳng chứa tia Ax.
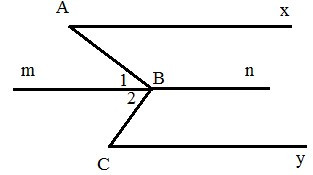
Vì nên (hai góc so le trong) (1)
Vì mà (giả thiết)
Do đó: (tính chất hai đường thẳng song song)
Vì nên (hai góc so le trong) (2)
Từ (1) và (2) ta có:
Mà
Vậy (đpcm)
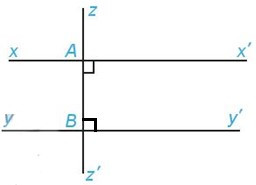
Bài 3. Vẽ hình, viết giả thiết, kết luận và chứng minh định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”.
Hướng dẫn giải
|
GT |
và là hai đường thẳng phân biệt tại A tại B |
|
KL |
|
Vì tại A nên
Vì tại B nên
Nên
Mà hai góc ở vị trí đồng vị.
Do đó (dấu hiệu nhận biết hai đường thẳng song song)
Xem thêm các bài giải Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Xem thêm các bài giải SGK Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Bài 10: Tiên đề Euclid. Tính chất của hai đường thẳng song song
Bài 11: Định lí và chứng minh định lí
Bài 12: Tổng các góc trong một tam giác