Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 7 Bài 11: Định lí và chứng minh định lí sách Kết nối tri thức. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 7. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Bài 11: Định lí và chứng minh định lí. Mời các bạn đón xem:
Bài tập Toán lớp 7 Bài 11: Định lí và chứng minh định lí
A. Bài tập Định lí và chứng minh định lí
A1. Bài tập tự luận
Bài 1. Vẽ hình, viết giả thiết, kết luận và chứng minh định lí: “Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông”.
Hướng dẫn giải
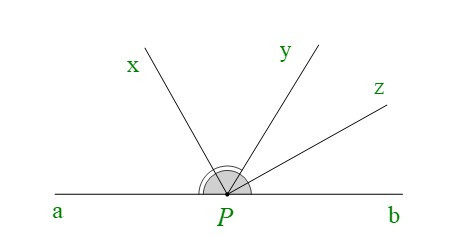
|
GT |
và là hai góc kề bù Px là tia phân giác của Pz là tia phân giác của |
|
KL |
là góc vuông |
Vì Px là tia phân giác của nên
Vì Pz là tia phân giác của nên
Nên
Mà ta có: + = 180° (hai góc kề bù)
Do đó:
Mặt khác:
Vậy , tức là là góc vuông.
Bài 2. Cho hình vẽ dưới đây. Biết Ax song song với Cy.
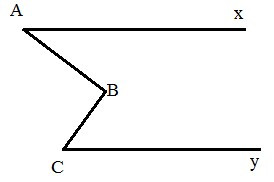
Chứng minh rằng
Hướng dẫn giải
|
GT |
|
|
KL |
|
Qua B, kẻ đường thẳng mn song song với đường thẳng chứa tia Ax.
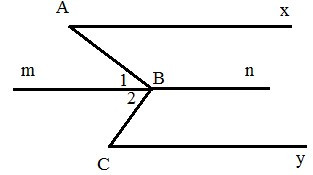
Vì nên (hai góc so le trong) (1)
Vì mà (giả thiết)
Do đó: (tính chất hai đường thẳng song song)
Vì nên (hai góc so le trong) (2)
Từ (1) và (2) ta có:
Mà
Vậy (đpcm)
Bài 3. Vẽ hình, viết giả thiết, kết luận và chứng minh định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”.
Hướng dẫn giải
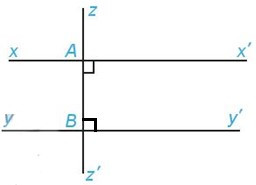
|
GT |
và là hai đường thẳng phân biệt tại A tại B |
|
KL |
|
Vì tại A nên
Vì tại B nên
Nên
Mà hai góc ở vị trí đồng vị.
Do đó (dấu hiệu nhận biết hai đường thẳng song song)
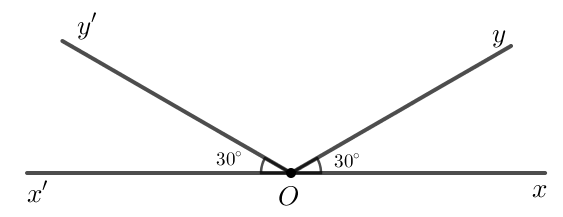
Bài 4. Hình tròn: Hai góc đối đỉnh thì chắc chắn bằng nhau rồi. Liệu hai góc bằng nhau thì có đối đỉnh không nhỉ?
Hình vuông: Tớ nghĩ đó là điều không đúng! Nhưng làm thế nào để khẳng định điều đó không đúng nhỉ?
Em có ý kiến gì về hai ý kiến trên?
Hướng dẫn giải
Hai góc bằng nhau thì chưa chắc đối đỉnh.
Hình vẽ bên dưới ta có =
= 30° nhưng hai góc này không đối đỉnh.
Bài 5. Hãy chứng minh định lí nói ở Ví dụ trang 56: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại”. Trong chứng minh đó ta đã sử dụng những điều đúng đã biết nào?
Hướng dẫn giải
Hình vẽ minh họa:
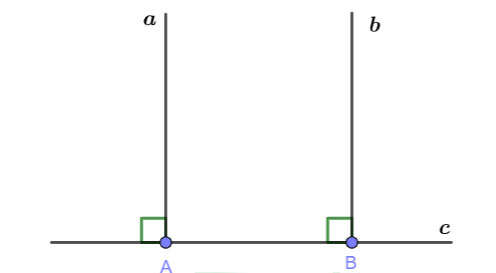
|
Giả thiết |
a // b, c vuông góc với a, c cắt a tại A, c cắt b tại B |
|
Kết luận |
c vuông góc với b |
Chứng minh
Ta có: c vuông góc với a =>
Mặt khác a // b => (Hai góc ở vị trí đồng vị)
=> c vuông góc với b
Bài 6. Cho góc xOy không phải là góc bẹt. Khẳng định nào sau đây đúng?
(1) Nếu Ot là tia phân giác của góc xOy thì
(2) Nếu tia Ot thỏa mãn thì Ot là tia phân giác của góc xOy.
Nếu có khẳng định không đúng, hãy nêu ví dụ cho thấy khẳng định đó không đúng. Gợi ý: Xét tia đối của một tia phân giác.
Hướng dẫn giải
(1) đúng vì Ot là tia phân giác của góc xOy thì
(2) sai vì
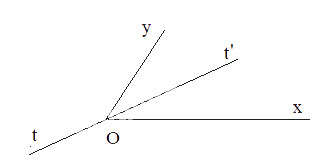
Ta có: nhưng Ot không là tia phân giác của góc xOy
Xét tia Ot’ là tia đối của tia Ot thì Ot’ là tia phân giác của góc xOy.
A2. Bài tập trắc nghiệm
Bài 7. Cho định lí: “Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại”.
Hình vẽ minh hoạ cho định lí trên là:
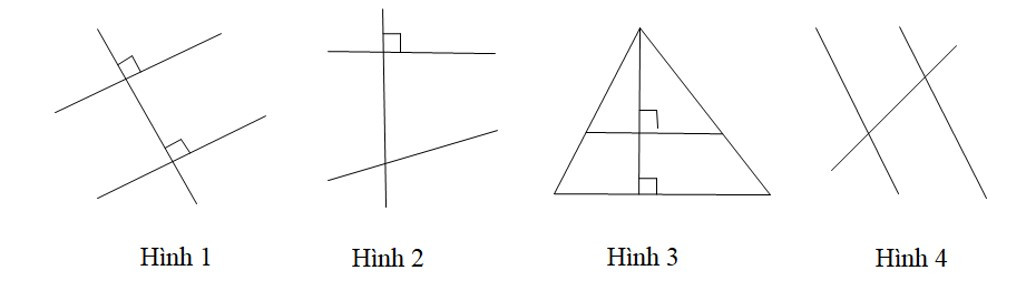
A. Hình 1, Hình 2;
B. Hình 2, Hình 3;
C. Hình 3, Hình 4;
D. Hình 1, Hình 3.
Hướng dẫn giải
Đáp án đúng là: D
Hình 2 không thỏa mãn điều kiện hai đường thẳng song song nên loại phương án A, B.
Hình 4 không thỏa mãn điều kiện vuông góc với một trong hai đường thẳng nên loại phương án C.
Hình 1, 3 thỏa mãn cả hai điều kiện trên.
Vậy chọn phương án D.
Bài 8. Phát biểu định lí sau bằng lời.
|
Giả thiết |
t cắt m tại A, t cắt n tại B và là hai góc đồng vị
|
|
Kết luận |
m // n |
A. Nếu đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì hai đường thẳng m, n vuông góc với nhau;
B. Nếu đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì hai đường thẳng m, n song song với nhau;
C. Nếu đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng m, n song song với nhau;
D. Nếu đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì hai đường thẳng m, n vuông góc với nhau.
Hướng dẫn giải
Đáp án đúng là: B
Nếu một đường thẳng t cắt hai đường thẳng m, n và trong số các góc tạo thành có một cặp góc đồng vị bằng nhau thì hai đường thẳng m, m song song với nhau.
Vậy chọn đáp án B.
Bài 9. Điền vào chỗ trống nội dung phù hợp.
 A. kết luận;
A. kết luận;
B. khẳng định;
C. chứng minh;
D. Cả 3 đáp án đều đúng.
Hướng dẫn giải
Đáp án đúng là: A
Phần nằm giữa từ “Nếu” và từ “thì” là phần giả thiết vậy phần nằm sau từ “thì” là phần kết luận.
Vậy chọn đáp án A.
B. Lý thuyết Định lí và chứng minh định lí
1. Định lí. Giả thiết và kết luận của định lí
• Định lí là một khẳng định được suy ra từ những khẳng định đúng đã biết. Mỗi định lí thường được phát biểu dưới dạng:
Nếu … thì …
+ Phần giữa từ “nếu” và từ “thì” là giả thiết của định lí.
+ Phần sau từ “thì” là kết luận của định lí.
Giả thiết, kết luận viết tắt tương ứng là GT và KL.
Ví dụ:
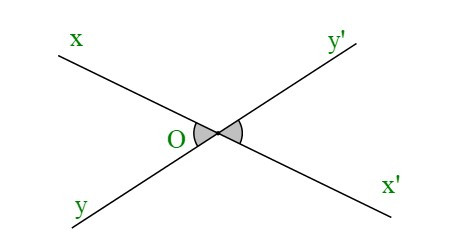
+ Định lí “Nếu hai góc đối đỉnh thì hai góc đó bằng nhau” được suy ra từ khẳng định đúng là “hai góc kề bù có tổng số đo bằng 180°).
Giả thiết là: hai góc đối đỉnh
Kết luận là: hai góc đó bằng nhau.
Ta viết giả thiết và kết luận của định lý trên bằng kí hiệu như sau:
|
GT |
và đối đỉnh |
|
KL |
= |
2. Chứng minh định lí
• Chứng minh một định lí là dùng lập luận để từ giả thiết và những khẳng định đúng đã biết suy ra kết luận của định lí.
Ví dụ:
+ Chứng minh định lí: “Nếu hai góc đối đỉnh thì hai góc đó bằng nhau” như sau:
|
GT |
và đối đỉnh |
|
KL |
= |
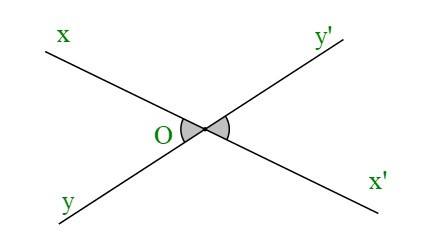
Ta có: + = 180° (hai góc kề bù)
= 180° − (1)
Lại có: + = 180° (hai góc kề bù)
= 180° − (2)
Từ (1) và (2) = (đpcm)
Chi là kon quỷ đến từ bình dưng
2023-11-04 18:00:40
?????Bổ ích quá. Trúng đề luôn mới ghê chứ. 5 sao UwU✨✨✨✨