Với giải Bài 5.6 trang 90 Toán 9 Tập 1 Kết nối tri thức chi tiết trong Bài 14: Cung và dây của một đường tròn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 14: Cung và dây của một đường tròn

Bài 5.6 trang 90 Toán 9 Tập 1: Cho đường tròn (O; 5 cm) và AB là một dây bất kì của đường tròn đó. Biết AB = 6 cm.

a) Tính khoảng cách từ O đến đường thẳng AB.

b) Tính tan α nếu góc ở tâm chắn cung AB bằng 2α.

Lời giải:

a) Gọi H là trung điểm của AB.

Suy ra $AH=\frac{AB}{2}=\frac{6}{2}=3\text{\hspace{0.17em}\hspace{0.17em}(cm)}.$

Xét ∆OAH và ∆OBH có:

OA = OB = R

Cạnh OH chung

HA = HB (do H là trung điểm của AB)

Do đó ∆OAH = ∆OBH (c.c.c).

Suy ra $\widehat{OHA}=\widehat{OHB}$  (hai góc tương ứng)

Mà $\widehat{OHA}$  và $\widehat{OHB}$  là hai góc bù nhau nên $\widehat{OHA}+\widehat{OHB}=180°$  hay $2\widehat{OHB}=180°$

Suy ra $\widehat{OHA}=\widehat{OHB}=90°$  nên OH ⊥ AB.

Do đó khoảng cách từ O đến đường thẳng AB bằng độ dài đoạn OH.

Xét tam giác OAH vuông tại H có:

AH² + OH² = OA² (định lý Pythagore)

Hay OH² = OA² − AH² = 5² − 3² = 16.

Nên OH = 4 cm.

Vậy khoảng cách từ O đến đường thẳng AB bằng 4 cm.

b) Theo giả thiết, góc ở tâm chắn cung AB là $\widehat{AOB}=2\alpha$ .

Từ câu a) ∆OAH = ∆OBH suy ra $\widehat{HOA}=\widehat{HOB}$  (hai góc tương ứng).

Lại có: $\widehat{HOA}+\widehat{HOB}=\widehat{AOB}$  nên $2\widehat{HOA}=2\alpha$  hay $\widehat{HOA}=\alpha .$

Suy ra $\tan \alpha =\frac{AH}{OH}=\frac{3}{4}.$

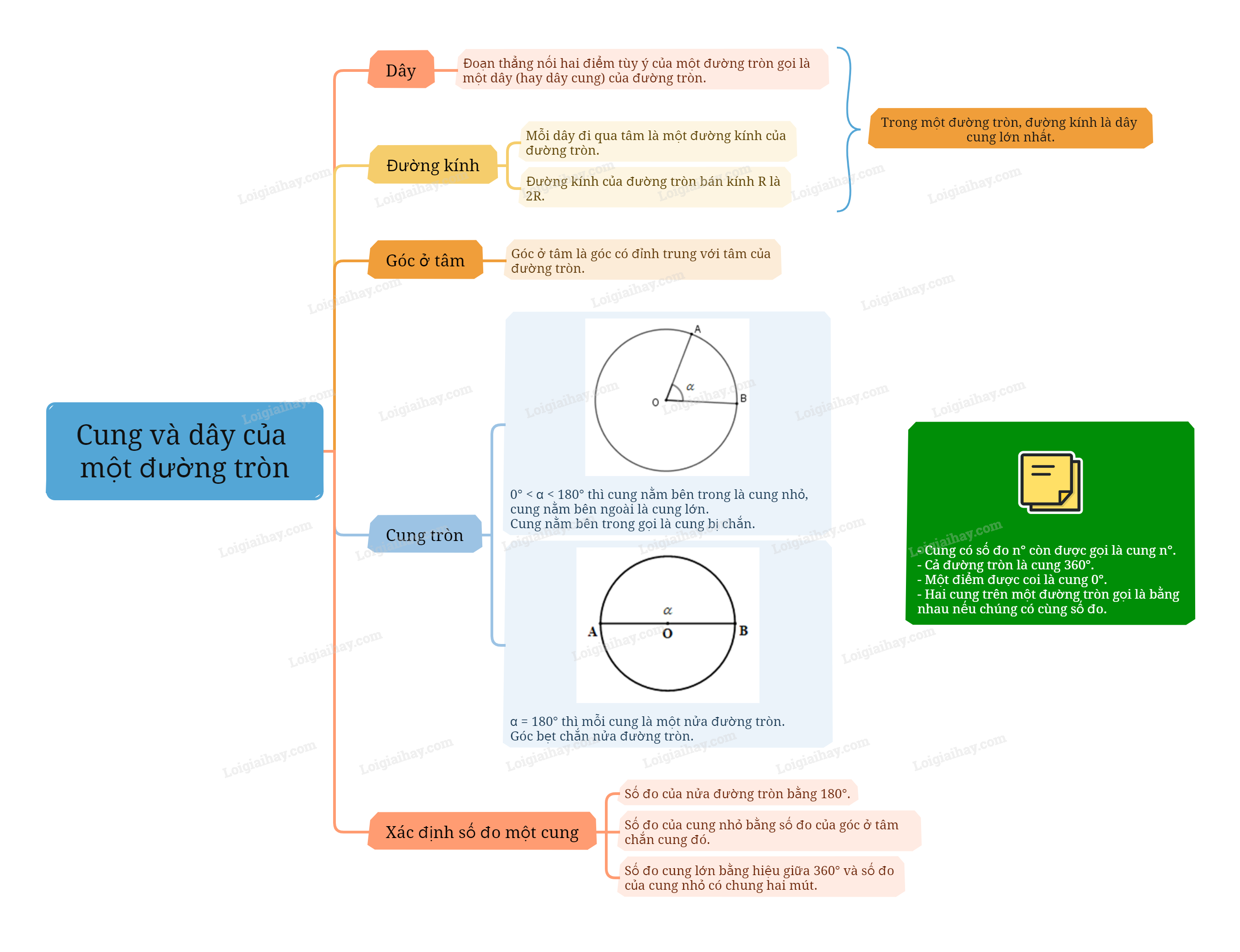
Sơ đồ tư duy Cung và dây của một đường tròn