Với giải Vận dụng 2 trang 86 Toán 9 Tập 1 Kết nối tri thức chi tiết trong Bài 13: Mở đầu về đường tròn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 13: Mở đầu về đường tròn

Vận dụng 2 trang 86 Toán 9 Tập 1: Trở lại tình huống mở đầu, bằng cách gấp mảnh giấy hình tròn theo hai cách khác nhau, Oanh có thể tìm được tâm của hình tròn. Em hãy làm thử xem.

Lời giải:

Gấp đôi hình tròn sao cho mép giấy của chúng đè khít lên nhau, ta miết phần ngăn cách hai nửa hình tròn ta được một đường kính.

Tiếp theo ta mở tờ giấy và gấp theo hướng khác và các mép giấy của hình tròn cũng đè khít lên nhau. Từ đó, xác định được đường kính mới.

Hai đường kính này cắt nhau tại một điểm chính là tâm của hình tròn.

Lý Thuyết Tính đối xứng của đường tròn

a) Đối xứng tâm

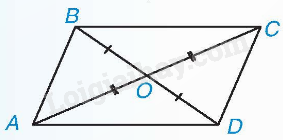
Hai điểm M và M’ gọi là đối xứng với nhau qua điểm I (hay qua tâm I) nếu I là trung điểm của đoạn MM’.

Ví dụ: Nếu O là giao điểm của hai đường chéo của hình bình hành ABCD thì

+) OA = OC nên A và C đối xứng với nhau.

+) OB = OD nên B và D đối xứng với nhau.

b) Đối xứng trục

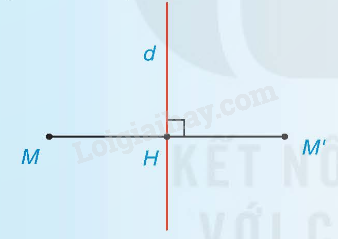
Hai điểm M và M’ gọi là đối xứng với nhau qua đường thẳng d (hay qua trục d) nếu d là đường trung trực của đoạn MM’.

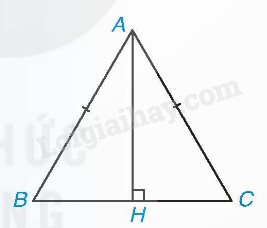
Ví dụ: Nếu AH là đường cao trong tam giác ABC cân tại A thì AH cũng là đường trung trực của BC, nên B và C đối xứng với nhau qua AH.

c) Tâm đối xứng của đường tròn

d) Trục đối xứng của đường tròn