Với giải Luyện tập 2 trang 86 Toán 9 Tập 1 Kết nối tri thức chi tiết trong Bài 13: Mở đầu về đường tròn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán 9 Bài 13: Mở đầu về đường tròn
Luyện tập 2 trang 86 Toán 9 Tập 1: Cho đường tròn tâm O và hai điểm A, B thuộc (O). Gọi d là đường trung trực của đoạn AB. Chứng minh rằng d là một trục đối xứng của (O).
Lời giải:
Vì hai điểm A, B thuộc (O) nên OA = OB.
Mà d là đường trung trực của đoạn AB nên nên O thuộc d.
Hay đường thẳng d đi qua tâm O của đường tròn.
Vậy d là một trục đối xứng của (O).
Lý Thuyết Tính đối xứng của đường tròn
a) Đối xứng tâm
Hai điểm M và M’ gọi là đối xứng với nhau qua điểm I (hay qua tâm I) nếu I là trung điểm của đoạn MM’.
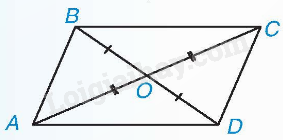
Ví dụ: Nếu O là giao điểm của hai đường chéo của hình bình hành ABCD thì
+) OA = OC nên A và C đối xứng với nhau.
+) OB = OD nên B và D đối xứng với nhau.
b) Đối xứng trục
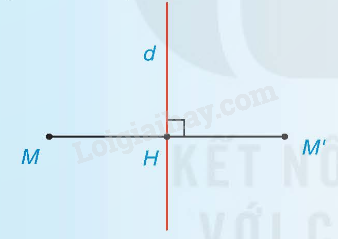
Hai điểm M và M’ gọi là đối xứng với nhau qua đường thẳng d (hay qua trục d) nếu d là đường trung trực của đoạn MM’.
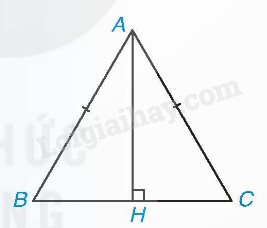
Ví dụ: Nếu AH là đường cao trong tam giác ABC cân tại A thì AH cũng là đường trung trực của BC, nên B và C đối xứng với nhau qua AH.
c) Tâm đối xứng của đường tròn
|
- Đường tròn là hình có tâm đối xứng; tâm của đường tròn là tâm đối xứng của nó. - Đường tròn có một tâm đối xứng. |
d) Trục đối xứng của đường tròn
|
- Đường tròn là hình có trục đối xứng; mỗi đường thẳng qua tâm của đường tròn là một trục đối xứng của nó. - Đường tròn có vô số trục đối xứng. |
Xem thêm lời giải bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:
HĐ trang 85 Toán 9 Tập 1: Chứng minh rằng nếu một điểm thuộc đường tròn (O) thì:......
Bài 5.4 trang 86 Toán 9 Tập 1: Cho hình vuông ABCD có E là giao điểm của hai đường chéo......
Xem thêm các bài giải bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:
Bài 14. Cung và dây của một đường tròn
Bài 15. Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
