Với giải sách bài tập Toán 9 Bài 13: Mở đầu về đường tròn sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:

Giải SBT Toán 9 Bài 13: Mở đầu về đường tròn

Bài 5.1 trang 56 sách bài tập Toán 9 Tập 1: Các bánh xe (xe đạp, ô tô,...) đều có dạng hình tròn (với tâm tại trục của bánh xe). Hãy giải thích lí do.

Lời giải:

Các bánh xe có dạng hình tròn để khi chuyển động, trục bánh xe luôn giữ một khoảng cách không đổi đối với mặt đường (bằng với bán kính bánh xe). Điều đó giúp người ngồi trên xe không bị mất thăng bằng (di chuyển lên xuống) trên đường bẳng phẳng.

Bài 5.2 trang 56 sách bài tập Toán 9 Tập 1: Cho đường tròn (O) có bán kính bằng 2,5 cm và hai tia Ox, Oy vuông góc với nhau tại O. Trên tia Ox lấy điểm A sao cho OA = 3 cm; trên tia Oy lấy điểm B sao cho OB = 4 cm. Gọi M là trung điểm của đoạn AB. Chứng minh rằng điểm M nằm trên đường tròn (O).

Lời giải:

Áp dụng định lý Pythagore vào tam giác vuông AOB ta có:

$AB=\sqrt{O{A}^2+O{B}^2}=\sqrt{3^2+4^2}=5$ (cm)

M là trung điểm AB nên $OM=MA=MB=\frac{AB}{2}=\frac{5}{2}=\mathrm{2,5}$(cm)

Mà bán kính đường tròn (O) là 2,5 cm nên điểm M nằm trên đường tròn (O). (đpcm)

Bài 5.3 trang 56 sách bài tập Toán 9 Tập 1: Trên mặt phẳng toạ độ Oxy, cho hai điểm A(0; –3) và B(2; 0). Gọi C và D là các điểm lần lượt đối xứng với A và B qua O.

a) Xác định toạ độ của hai điểm C và D.

b) Xác định vị trí của các điểm A, B, C và D đối với đường tròn (O; 3).

Lời giải:

a) Điểm C đối xứng với A qua O nên điểm C có hoành độ và tung độ là số đối với hoành độ và tung độ của điểm A. Suy ra tọa độ điểm C là C(0; 3).

Điểm D đối xứng với B qua O nên điểm D có hoành độ và tung độ là số đối với hoành độ và tung độ của điểm B. Suy ra tọa độ điểm C là C(–2; 0).

b) Vì OA = OC = 3 nên A và C nằm trên đường tròn (O; 3).

Vì OB = OD = 2 < 3 nên B và D nằm trong đường tròn (O; 3).

Bài 5.4 trang 56 sách bài tập Toán 9 Tập 1: Trên mặt phẳng toạ độ Oxy, cho điểm A(3; 1). Gọi B, C và D là các điểm đối xứng với A lần lượt qua trục hoành, qua gốc O và qua trục tung.

a) Xác định toạ độ của ba điểm B, C và D.

b) Có hay không một đường tròn đi qua bốn điểm A, B, C và D. Xác định tâm và bán kính của đường tròn đó, nếu có.

Lời giải:

a) + Điểm B đối xứng với A qua trục hoành nên A và B có cùng hoành độ, tung độ của B là số đối của tung độ của A. Suy ra tọa độ điểm B là B(3; –1).

+ Điểm D đối xứng với A qua trục tung nên A và D có cùng tung độ, hoành độ của D là số đối của hoành độ của A. Suy ra tọa độ điểm D là B(–3; 1).

+ Điểm C đối xứng với A qua O nên tung độ, hoành độ của C là số đối của tung độ, hoành độ của A. Suy ra tọa độ điểm C là B(–3; –1).

b) Ta thấy: $OA=OB=OC=OD=\sqrt{3^2+1^2}=\sqrt{10}$

Vậy 4 điểm A, B, C, D cùng nằm trên đường tròn $\left(O;\sqrt{10}\right)$

Bài 5.5 trang 56 sách bài tập Toán 9 Tập 1: Cho đường tròn (O), đường kính AB và điểm M thuộc (O) (M không trùng với điểm nào trong hai điềm A và B). Trên (O) lấy điểm N nằm khác phía của M đối với đường thẳng AB sao cho AM = BN. Chứng minh rằng O là trung điểm của đoạn MN.

Lời giải:

Xét ∆AOM và ∆BON có

Ta thấy: OM = ON (bán kính đường tròn (O))

OA = OB (bán kính đường tròn (O))

AM = BN (theo đề bài)

Do đó ∆AOM = ∆BON (c.c.c), suy ra $\widehat{AOM}=\widehat{BON}$

Ta có: $\widehat{AOM}+\widehat{MOB}=180°$(do A, O, B thẳng hàng).

Mà $\widehat{AOM}=\widehat{BON}$ nên $\widehat{BON}+\widehat{MOB}=180°$, suy ra ba điểm M, O, N thẳng hàng.

Mà OM = ON nên 3 điểm O là trung điểm của MN. (đpcm)

Lý thuyết Mở đầu về đường tròn

1. Đường tròn

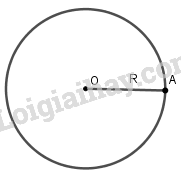
Định nghĩa đường tròn

Khi không cần để ý đến bán kính ta kí hiệu đường tròn tâm O là (O).

Điểm thuộc đường tròn

Nếu A là một điểm của đường tròn (O) thì ta viết $A\in \left(O\right)$. Khi đó, ta còn nói đường  tròn (O) đi qua điểm A, hay điểm A nằm trên đường tròn (O).

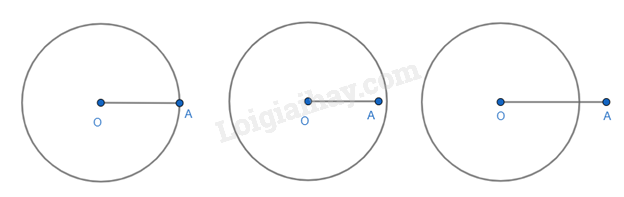
Tổng quát:

- Điểm A nằm trên đường tròn (O; R) nếu OA = R;

- Điểm A nằm trong đường tròn (O; R) nếu OA < R;

- Điểm A nằm ngoài đường tròn (O; R) nếu OA > R.

Hình tròn tâm O bán kính R là hình gồm các điểm nằm trên và nằm trong đường tròn (O;R).

2. Tính đối xứng của đường tròn

a) Đối xứng tâm

Hai điểm M và M’ gọi là đối xứng với nhau qua điểm I (hay qua tâm I) nếu I là trung điểm của đoạn MM’.

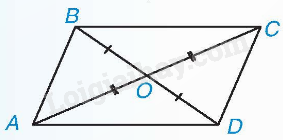
Ví dụ: Nếu O là giao điểm của hai đường chéo của hình bình hành ABCD thì

+) OA = OC nên A và C đối xứng với nhau.

+) OB = OD nên B và D đối xứng với nhau.

b) Đối xứng trục

Hai điểm M và M’ gọi là đối xứng với nhau qua đường thẳng d (hay qua trục d) nếu d là đường trung trực của đoạn MM’.

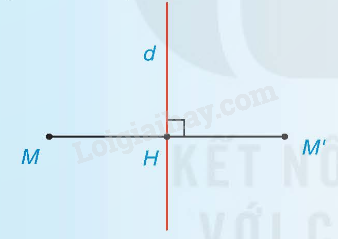
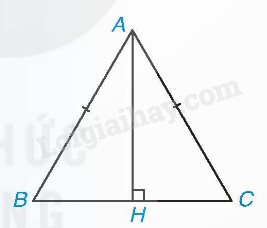
Ví dụ: Nếu AH là đường cao trong tam giác ABC cân tại A thì AH cũng là đường trung trực của BC, nên B và C đối xứng với nhau qua AH.

c) Tâm đối xứng của đường tròn

d) Trục đối xứng của đường tròn

Xem thêm các bài giải SBT Toán lớp 9 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 4

Bài 13: Mở đầu về đường tròn

Bài 14: Cung và dây của một đường tròn

Bài 15: Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên

Bài 16: Vị trí tương đối của đường thẳng và đường tròn

Bài 17: Vị trí tương đối của hai đường tròn