Với giải Luyện tập 1 trang 84 Toán 9 Tập 1 Kết nối tri thức chi tiết trong Bài 13: Mở đầu về đường tròn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán 9 Bài 13: Mở đầu về đường tròn
Luyện tập 1 trang 84 Toán 9 Tập 1: Cho tam giác ABC vuông tại A. Chứng minh rằng điểm A thuộc đường tròn đường kính BC.
Lời giải:
Gọi O là trung điểm của BC.
Ta có AO là trung tuyến ứng với cạnh huyền nên
Suy ra A, B, C cùng thuộc đường tròn bán kính OA.
Tâm O là trung điểm của BC nên BC là đường kính.
Vậy điểm A thuộc đường tròn đường kính BC.
Lý Thuyết Đường tròn
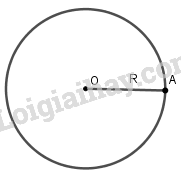
Định nghĩa đường tròn
|
Đường tròn tâm O bán kính R (R > 0), kí hiệu là (O; R), là hình gồm tất cả các điểm cách điểm O một khoảng bằng R. |
Khi không cần để ý đến bán kính ta kí hiệu đường tròn tâm O là (O).
Điểm thuộc đường tròn
Nếu A là một điểm của đường tròn (O) thì ta viết . Khi đó, ta còn nói đường tròn (O) đi qua điểm A, hay điểm A nằm trên đường tròn (O).
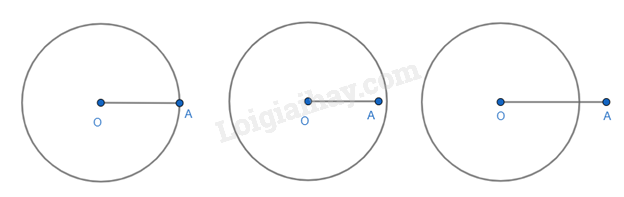
Tổng quát:
- Điểm A nằm trên đường tròn (O; R) nếu OA = R;
- Điểm A nằm trong đường tròn (O; R) nếu OA < R;
- Điểm A nằm ngoài đường tròn (O; R) nếu OA > R.
Hình tròn tâm O bán kính R là hình gồm các điểm nằm trên và nằm trong đường tròn (O;R).
Xem thêm lời giải bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:
HĐ trang 85 Toán 9 Tập 1: Chứng minh rằng nếu một điểm thuộc đường tròn (O) thì:......
Bài 5.4 trang 86 Toán 9 Tập 1: Cho hình vuông ABCD có E là giao điểm của hai đường chéo......
Xem thêm các bài giải bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:
Bài 14. Cung và dây của một đường tròn
Bài 15. Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
