Với giải Khám phá 3 trang 101 Toán 9 Tập 1 Chân trời sáng tạo chi tiết trong Bài 4: Hình quạt tròn và hình vành khuyên giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán 9 Bài 4: Hình quạt tròn và hình vành khuyên
Khám phá 3 trang 101 Toán 9 Tập 1: a) Vẽ đường tròn (C) tâm O bán kính r = 5 cm và đường tròn (C’) tâm O bán kính R = 8 cm.
b) Tính diện tích S của (C) và diện tích S’ của (C’).
c) Hãy cho biết hiệu số (S’ – S) biểu diễn diện tích của phần nào trên Hình 9.
Lời giải:
a)
b) Diện tích S của đường tròn (C) là: S = π.52 = 25π (cm2).
Diện tích S’ của đường tròn (C’) là: S’ = π.82 = 64π (cm2).
c) Hiệu số (S’ – S) biểu diễn diện tích phần giới hạn bởi hai đường tròn (C) và (C’).
Lý Thuyết Hình vành khuyên
Khái niệm hình vành khuyên
|
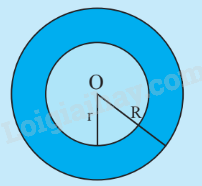
Cho hai đường tròn đồng tâm và với . Hình vành khuyên là phần mặt phẳng giới hạn bởi hai đường tròn (O;r) và (O;R) được tính bởi công thức: . |
Diện tích hình vành khuyên
|
Diện tích của hình vành khuyên tạo bởi hai đường tròn đồng tâm và có bán kính R và r: (với R > r) |
Ví dụ: Diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 3m và 5m là:
Xem thêm lời giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:
Thực hành 1 trang 99 Toán 9 Tập 1: Tính độ dài cung 72° của một đường tròn có bán kính 25 cm........
Bài 1 trang 102 Toán 9 Tập 1: Tính độ dài các cung 30°; 90°; 120° của đường tròn (O; 6 cm)........
Xem thêm các bài giải bài tập Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:
Bài 3. Góc ở tâm, góc nội tiếp
Bài 4. Hình quạt tròn và hình vành khuyên
Hoạt động 1. Làm giác kế đo góc nâng đơn giản
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
