Với giải sách bài tập Toán 9 Bài 4: Hình quạt tròn và hình vành khuyên sách Chân trời sáng tạo hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 9. Mời các bạn đón xem:
Giải SBT Toán 9 Bài 4: Hình quạt tròn và hình vành khuyên
Bài 1 trang 96 sách bài tập Toán 9 Tập 1: Quan sát Hình 8 và tính:
a) số đo cung AmB.
b) độ dài cung AmB.
c) diện tích hình quạt tròn OAmB.
d) diện tích hình viên phân giới hạn bởi cung AmB và dây AB.
Lời giải:
a) Xét ∆OAB cân tại O (do OA = OB) nên
Suy ra
b) Độ dài cung AmB là:
c) Diện tích hình quạt tròn OAmB là:
d) Do ∆OAB có nên ∆OAB vuông tại O.
Diện tích tam giác OAB là:
Diện tích hình viên phân giới hạn bởi cung AmB và dây AB bằng:
SOAmB – S∆OAB = π – 2 ≈ 3,14 – 2 = 1,14 (cm2).
Bài 2 trang 97 sách bài tập Toán 9 Tập 1: Cho đường tròn (O) đường kính AB = 3 cm, (Hình 9).
a) Tính độ dài cung BmD.
b) Tính diện tích hình quạt tròn OBmD.
Lời giải:
a) Xét ∆OAC cân tại O (do OA = OC), suy ra
Lại có
Suy ra
Do đó (đối đỉnh).
Do AB = 3 cm, suy ra (cm).
Cung BmD có số đo 120°, bán kính R = 1,5 cm có độ dài là:
b) Diện tích hình quạt tròn OBmD bán kính R = 1,5 cm là:
Bài 3 trang 97 sách bài tập Toán 9 Tập 1: Một biểu đồ hình quạt tròn được vẽ trong đường tròn bán kính R = 15 cm (Hình 10). Tính diện tích của mỗi hình quạt tròn trong biểu đồ đó.
Lời giải:
Diện tích hình quạt tròn ứng với số liệu 45% là:
Diện tích hình quạt tròn ứng với số liệu 33 % là:
Diện tích hình quạt tròn ứng với số liệu 22 % là:
Bài 4 trang 97 sách bài tập Toán 9 Tập 1: Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 8 cm) và (O; 24 cm).
Lời giải:
Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 8 cm) và (O; 24 cm) là:
S = π(R2 – r2) = π(242 – 82) = 512π ≈ 1 608,50 (cm2).
Bài 5 trang 97 sách bài tập Toán 9 Tập 1: Hai trạm phát sóng A và B đặt cách nhau 100 km. Trạm phát sóng A và trạm phát sóng B có bán kính hoạt động lần lượt là 50 km và Tính diện tích của khu vực có thể đặt thiết bị thu sóng sao cho thu được cả hai sóng phát từ trạm A và trạm B. Biết rằng nếu khoảng cách từ thiết bị thu sóng đến trạm phát sóng lớn hơn bán kính hoạt động của trạm phát sóng thì thiết bị không thu được sóng của trạm phát sóng đó.
Lời giải:
Gọi C và D là giao điểm của hai đường tròn (A; 50 km) và
Ta có:
AB2 = 1002 = 10 000.
Ta thấy AC2 + BC2 = AB2, suy ra ∆ABC vuông tại C (định lí Pythagore đảo).
Xét ∆ABC vuông tại C có:
suy ra
Suy ra
Tương tự, ta có:
Do đó
Xét ∆BCD có BC = BD và nên là tam giác đều, suy ra
Diện tích của hình quạt tròn ACD được giới hạn bởi bán kính AC, bán kính AD và cung nhỏ CD của đường tròn (A; 50 km) là:
Diện tích hình quạt tròn BCD được giới hạn bởi bán kính BC, bán kính BD và cung nhỏ CD của đường tròn là:
Diện tích tứ giác ABCD là:
Diện tích của khu vực có thể đặt thiết bị thu sóng sao cho thu được cả hai sóng phát từ trạm A và trạm B là
Bài 6 trang 97 sách bài tập Toán 9 Tập 1: Một ống thép có đường kính ngoài là 100 mm và đường kính trong là 80 mm. Tính diện tích mặt cắt ngang của ống thép đó.
Lời giải:
Bán kính ngoài của ống thép là:
Bán kính trong của ống thép là:
Mặt cắt ngang của ống thép có hình vành khuyên giới hạn bởi hai đường tròn (O; 50 mm) và (O; 40 mm) nên có diện tích:
S = π(R2 – r2) = π(502 – 402) = 900π ≈ 2 827,43 (mm2) .
Bài 7 trang 97 sách bài tập Toán 9 Tập 1: Một chiếc bàn hình tròn được ghép bởi hai nửa hình tròn đường kính AB = 1,2 m. Người ta muốn nới rộng mặt bàn bằng cách ghép thêm vào giữa một mặt hình chữ nhật có một kích thước là 1,2 m.
a) Kích thước còn lại của hình chữ nhật phải là bao nhiêu nếu diện tích mặt bàn tăng gấp đôi sau khi nới?
b) Kích thước còn lại của hình chữ nhật phải là bao nhiêu nếu chu vi mặt bàn tăng gấp đôi sau khi nới?
Lời giải:
a) Bán kính của chiếc bàn hình tròn ban đầu là:
Diện tích mặt bàn ban đầu là:
Theo bài, diện tích mặt bàn tăng gấp đôi sau khi nới nên diện tích phần mặt bàn hình chữ nhật bằng diện tích mặt bàn ban đầu, và bằng
Kích thước còn lại của hình chữ nhật là:
b) Chu vi mặt bàn ban đầu là:
Theo bài, chu vi mặt bàn tăng gấp đôi sau khi nới và phần chu vi tăng lên chính là hai lần độ dài cạnh còn lại của phần mặt bàn hình chữ nhật và bằng
Kích thước còn lại của hình chữ nhật là:
Bài 8 trang 98 sách bài tập Toán 9 Tập 1: Một vườn cỏ có dạng hình chữ nhật ABCD với AB = 40 m, AD = 30 m. Người ta muốn buộc hai con dê ở hai góc vườn A, B. Có hai cách buộc:
Cách 1: Mỗi dây thừng dài 20 m.
Cách 2: Một dây thừng dài 30 m và một dây thừng dài 10 m.
Hỏi với cách buộc nào thì diện tích cỏ mà hai con dê có thể ăn được sẽ lớn hơn?
Lời giải:
Diện tích cỏ hai con dê có thể ăn là dạng hai hình quạt có số đo cung cùng bằng 90°.
Truờng hợp 1: Mỗi dây thừng dài 20 m suy ra R1 = R2 = 20 m.
Diện tích cỏ mà hai con dê có thể ăn là:
Truờng hợp 2: Giả sử dây thừng cột con dê ở A dài 30 m, dây thừng cột con dê ở B dài 10 m, suy ra R1 = 30 m, R2 = 10 m.
Diện tích cỏ mà hai con dê có thể ăn là:
Ta thấy 250π > 200π nên S’ > S.
Vậy dùng hai sợi dây 30 m và 10 m thì diện tích cỏ hai con dê ăn sẽ nhiều hơn.
Lý thuyết Hình quạt tròn và hình vành khuyên
1. Độ dài cung tròn
Công thức tính chu vi đường tròn
Công thức tính độ dài C của đường tròn (O; R), đường kính d = 2R là:
Công thức tính độ dài cung tròn
|
Trên đường tròn bán kính R, độ dài l của một cung có số đo được tính theo công thức: . |
Ví dụ:
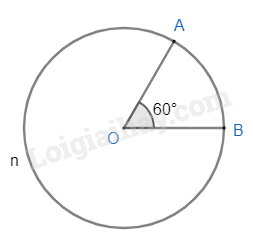
Đường tròn (O; 2cm), .
- Cung nhỏ AB bị chắn bởi góc ở tâm AOB.
Do đó sđ
Độ dài của cung AB là:
Cung lớn AnB có số đo là:
sđ.
Độ dài của cung AnB là:
2. Hình quạt tròn
Khái niệm hình quạt tròn
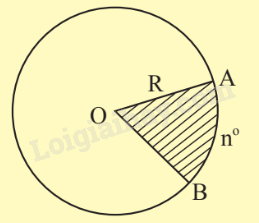
|
Hình quạt tròn là một phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai mút của cung đó. |
Diện tích hình quạt tròn
|
Diện tích hình quạt tròn bán kính R ứng với cung :
|
Ví dụ: Diện tích hình quạt tròn có độ dài tương ứng với nó là cm, bán kính là R = 5cm là:
3. Hình vành khuyên
Khái niệm hình vành khuyên
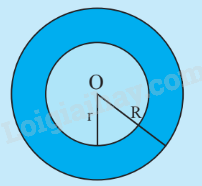
|
Cho hai đường tròn đồng tâm và với . Hình vành khuyên là phần mặt phẳng giới hạn bởi hai đường tròn (O;r) và (O;R) được tính bởi công thức: . |
Diện tích hình vành khuyên
|
Diện tích của hình vành khuyên tạo bởi hai đường tròn đồng tâm và có bán kính R và r: (với R > r) |
Ví dụ: Diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 3m và 5m là:
Xem thêm các bài giải SBT Toán lớp 9 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Tiếp tuyến của đường tròn
Bài 3: Góc ở tâm, góc nội tiếp
Bài 4: Hình quạt tròn và hình vành khuyên