Với giải Khám phá 1 trang 98 Toán 9 Tập 1 Chân trời sáng tạo chi tiết trong Bài 4: Hình quạt tròn và hình vành khuyên giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 4: Hình quạt tròn và hình vành khuyên

Khám phá 1 trang 98 Toán 9 Tập 1: Một hàng rào bao quanh một sân cỏ hình tròn có bán kính 10 m (Hình 1) được ghép bởi 360 phần bằng nhau. Hãy tính:

a) Độ dài của toàn bộ hàng rào.

b) Độ dài của mỗi phần hàng rào.

c) Độ dài của n phần hàng rào.

Lời giải:

a) Độ dài củ toàn bộ hàng rào (chu vi của đường tròn) là: 2π.10 = 20π (m).

b) Độ dài của mỗi phần hàng rào là: $\frac{20\pi }{360}=\frac{\pi }{18}$ (m).

c) Độ dài của n phần hàng rào là: $n\cdot \frac{\pi }{18}$ (m).

Lý Thuyết Độ dài cung tròn

Công thức tính chu vi đường tròn

Công thức tính độ dài C của đường tròn (O; R), đường kính d = 2R là:

$C=\pi d=2\pi R$

Công thức tính độ dài cung tròn

Ví dụ:

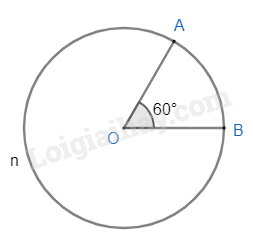
Đường tròn (O; 2cm), $\widehat{AOB}={60}^0$.

- Cung nhỏ AB bị chắn bởi góc ở tâm AOB.

Do đó sđ$\stackrel{⌢}{AB}=\widehat{AOB}={60}^0$

Độ dài $l_1$ của cung AB là:

$l_1=\frac{n}{180}\pi R=\frac{60}{180}\pi .2=\frac{2\pi }{3}\approx 2,1\left(cm\right)$

Cung lớn AnB có số đo là:

sđ$\stackrel{⌢}{AmN}={360}^o-{60}^0={300}^0$.

Độ dài $l_2$ của cung AnB là:

$l_2=\frac{300}{180}\pi .2=\frac{10}{3}\pi \approx 10,5\left(cm\right)$