Với giải Luyện tập 1 trang 77 Toán 9 Tập 1 Cánh diều chi tiết trong Bài 1: Tỉ số lượng giác của góc nhọn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán 9 Bài 1: Tỉ số lượng giác của góc nhọn
Luyện tập 1 trang 77 Toán 9 Tập 1: Cho tam giác MNP vuông tại M, MN = 3 cm, MP = 4 cm. Tính độ dài cạnh NP và các tỉ số lựợng giác của góc P.
Lời giải:

Xét ∆MNP vuông tại M, theo định lí Pythagore, ta có:
NP2 = MN2 + MP2 = 32 + 42 = 25.
Suy ra NP = 5 (cm) (do NP > 0).
Theo định nghĩa tỉ số lượng giác, ta có:
sinP = ;
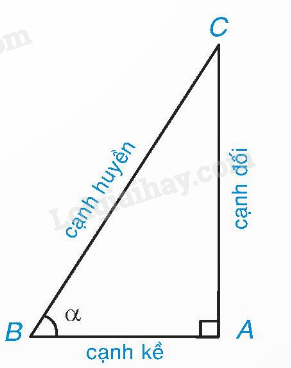
Lý thuyết Tỉ số lượng giác của một góc nhọn
|
.
gọi là các tỉ số lượng giác của góc nhọn .
|
Tip học thuộc nhanh:
|
Sin đi học
Cos không hư
Tan đoàn kết
Cotang kết đoàn
|
Ví dụ:
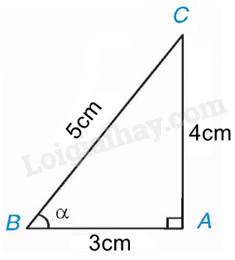
Theo định nghĩa của tỉ số lượng giác, ta có:
, , ,
Xem thêm lời giải bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:
Khởi động trang 74 Toán 9 Tập 1: Cho góc nhọn Xét tam giác ABC vuông tại A, tam giác A’BC’ vuông tại A’ với A, A’ thuộc tia Bx và C, C’ thuộc tia By (Hình 1). Do ∆ABC ᔕ ∆A’BC’ nên ......
Hoạt động 1 trang 74 Toán 9 Tập 1: Cho tam giác ABC vuông tại A có (Hình 2).......
Luyện tập 1 trang 77 Toán 9 Tập 1: Cho tam giác MNP vuông tại M, MN = 3 cm, MP = 4 cm. Tính độ dài cạnh NP và các tỉ số lựợng giác của góc P.......
Hoạt động 2 trang 77 Toán 9 Tập 1: Cho tam giác ABC vuông tại A (Hình 7).......
Luyện tập 2 trang 78 Toán 9 Tập 1: Tính:......
Luyện tập 3 trang 78 Toán 9 Tập 1: Sử dụng bảng tỉ số lượng giác của các góc nhọn đặc biệt, tính giá trị của biểu thức:......
Hoạt động 3 trang 79 Toán 9 Tập 1: Cùng với đơn vị đo góc là độ (kí hiệu: °), người ta còn sừ dụng những đơn vị đo góc khác là: phút (kí hiệu: ’), giây (kí hiệu: ”), với quy ước: 1° = 60’ ; 1’ = 60’’......
Hoạt động 4 trang 79 Toán 9 Tập 1: Sử dụng tính chất cotα = tan(90° – α), ta có thể tính được côtang của một góc nhọn. Chẳng hạn ta tính cot56° như sau:.....
Luyện tập 4 trang 79 Toán 9 Tập 1: Sử dụng máy tính cầm tay để tính (gần đúng) các giá trị lượng giác sau:......
Bài 1 trang 81 Toán 9 Tập 1: Cho tam giác ABC vuông tại A có AC = 4 cm, BC = 6 cm. Tính các tỉ số lượng giác của góc B.......
Bài 2 trang 81 Toán 9 Tập 1: Cho tam giác ABC vuông tại A có AB = 2 cm, AC = 3 cm. Tính các tỉ số lượng giác của góc C.......
Bài 3 trang 81 Toán 9 Tập 1: Cho tam giác MNP có MN = 5 cm, MP = 12 cm, NP = 13 cm. Chứng minh tam giác MNP vuông tại M. Từ đó, tính các tỉ số lượng giác của góc N.......
Bài 4 trang 81 Toán 9 Tập 1: Mỗi tỉ số lượng giác sau đây bằng tỉ số lượng giác nào của góc 63°? Vì sao?......
Bài 5 trang 81 Toán 9 Tập 1: Sử dụng máy tính cầm tay để tính các tỉ số lượng giác của mỗi góc sau (làm tròn kết quả đến hàng phần trăm):......
Bài 6 trang 81 Toán 9 Tập 1: Sử dụng tỉ số lượng giác của hai góc phụ nhau, tính giác trị biểu thức:.....
Bài 7 trang 81 Toán 9 Tập 1: Cho góc nhọn α. Biết rằng, tam giác ABC vuông tại A sao cho .....
Bài 8 trang 81 Toán 9 Tập 1: Hình 10 mô tả tia nắng mặt trời dọc theo AB tạo với phương nằm ngang trên mặt đất một góc Sử dụng máy tính cầm tay, tính số đo góc α (làm tròn kết quả đến hàng đơn vị của độ) biết AH = 2 m, BH = 5 m......
Xem thêm các bài giải bài tập Toán lớp 9 Cánh diều hay, chi tiết khác:
Bài tập cuối chương 3
§1. Tỉ số lượng giác của góc nhọn
§2. Một số hệ thức về cạnh và góc trong tam giác vuông
§3. Ứng dụng của tỉ số lượng giác của góc nhọn
Bài tập cuối chương 4
§1. Đường tròn. Vị trí tương đối của hai đường tròn

