Với giải Vận dụng trang 28 Toán 9 Tập 1 Kết nối tri thức chi tiết trong Bài 4: Phương trình quy về phương trình bậc nhất một ẩn giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:

Giải bài tập Toán 9 Bài 4: Phương trình quy về phương trình bậc nhất một ẩn

Vận dụng trang 28 Toán 9 Tập 1: Giải bài toán ở tình huống mở đầu.

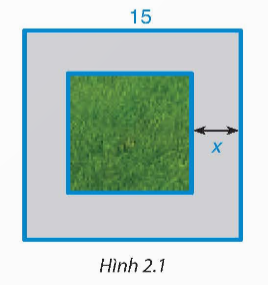
Tình huống mở đầu: Trong một khu vườn hình vuông có cạnh bằng 15m người ta làm một lối đi xung quanh vườn có bề rộng là x (m) (H.2.1). Để diện tích phần đất còn lại là $169m^2$ thì bề rộng x của lối đi là bao nhiêu?

Lời giải:

Do lối đi có bề rộng là x nên cạnh của khu vườn hình vuông ban đầu giảm đi $2x\left(m\right).$

Nên phần đất còn lại là hình vuông có cạnh $15-2x\left(m\right)$

Diện tích phần đất còn lại là $169m^2$ nên ta có phương trình ${\left(15-2x\right)}^2=169$

$\begin{array}{l}{\left(15-2x\right)}^2={13}^2\\ TH1:15-2x=13\\ 2x=2\\ x=1\end{array}$

$TH2:15-2x=-13$ (vô lý vì cạnh của mảnh đất >0)

Vậy $x=1$

Vậy bề rộng của lối đi là 1m.

Lý Thuyết Phương trình tích

Cách giải phương trình tích

Ví dụ: Giải phương trình $\left(2x+1\right)\left(3x-1\right)=0$

Lời giải:

Ta có: $\left(2x+1\right)\left(3x-1\right)=0$

nên $2x+1=0$ hoặc $3x-1=0$.

$2x+1=0$ hay $2x=-1$, suy ra $x=-\frac{1}{2}$.

$3x-1=0$ hay $3x=1$, suy ra $x=\frac{1}{3}$.

Vậy phương trình đã cho có hai nghiệm là $x=-\frac{1}{2}$ và $x=\frac{1}{3}$.

Các bước giải phương trình:

Ví dụ: Giải phương trình $x^2-x=-2x+2$.

Lời giải:

Biến đổi phương trình đã cho về phương trình tích như sau:

$\begin{array}{l}{x}^2-x=-2x+2\\ x^2-x+2x-2=0\\ x\left(x-1\right)+2\left(x-1\right)=0\\ \left(x+2\right)\left(x-1\right)=0.\end{array}$

Ta giải hai phương trình sau:

$x+2=0$ suy ra $x=-2$.

$x-1=0$ suy ra $x=1$.

Vậy phương trình đã cho có hai nghiệm là $x=-2$ và $x=1$.