Luyện tập 6 trang 52 Toán 12 Tập 1 Kết nối tri thức | Giải bài tập Toán 12

Luyện tập 6 trang 52 Toán 12 Tập 1 Kết nối tri thức | Giải bài tập Toán 12

Trịnh Thị Thu Hiền Ngày: 28-03-2024 Lớp 12

386

Với giải Luyện tập 6 trang 52 Toán 12 Tập 1 Kết nối tri thức chi tiết trong Bài 6: Vectơ trong không gian giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 12. Mời các bạn đón xem:

Giải bài tập Toán 12 Bài 6: Vectơ trong không gian

Luyện tập 6 trang 52 Toán 12 Tập 1: Trong Ví dụ 6, chứng minh rằng:

a) $\vec{B N}$ và $\vec{D M}$ là hai vectơ đối nhau;

b) $\vec{S D} - \vec{B N} - \vec{C M} = \vec{S C}$

Lời giải:

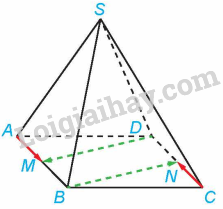
Tài liệu VietJack

a) Tứ giác ABCD là hình bình hành nên $A B = C D$ , AB//CD. Suy ra $B M = D N$ (vì M, N lần lượt là trung điểm của AB và CD) và BM//DN. Do đó, tứ giác DMBN là hình bình hành, do đó, $B N = D M$ và BN//DM. Hai vectơ $\vec{B N}$ và $\vec{D M}$ có cùng độ dài và ngược hướng nên $\vec{B N}$ và $\vec{D M}$ là hai vectơ đối nhau.

b) Theo a ta có: $\vec{B N} = - \vec{D M}$

Do đó, $\vec{S D} - \vec{B N} - \vec{C M} = \vec{S D} + \vec{D M} + \vec{M C} = \vec{S M} + \vec{M C} = \vec{S C}$

Xem thêm lời giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

HĐ1 trang 46 Toán 12 Tập 1: Trong Hình 2.2, lực căng dây (được tạo ra bởi sức nặng của kiện hàng) được thể hiện bởi các đoạn thẳng có mũi tên màu đỏ........

Câu hỏi trang 6 Toán 12 Tập 1: Hình 2.3 cho ta ví dụ về một số đại lượng có thể biểu diễn bởi vectơ trong không gian. Hãy tìm thêm một số ví dụ tương tự........

Luyện tập 1 trang 47 Toán 12 Tập 1: Cho hình lập phương ABCD.A’B’C’D’ (H.2.6). Trong các vectơ $\vec{A C}, \vec{A D}, \vec{A D^{'}}$ :.....

HĐ2 trang 47 Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’ (H.2.7).......

Câu hỏi trang 47 Toán 12 Tập 1: Nếu hai vectơ cùng bằng một vectơ thứ ba thì hai vectơ đó có bằng nhau không?......

Luyện tập 2 trang 48 Toán 12 Tập 1: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành.......

Vận dụng 1 trang 48 Toán 12 Tập 1: Một tòa nhà có chiều cao của các tầng là như nhau. Một chiếc thang máy di chuyển từ tầng 15 lên tầng 22 của tòa nhà, sau đó di chuyển từ tầng 22 lên tầng 29. Các vectơ biểu diễn độ dịch chuyển của thang máy trong hai lần di chuyển đó có bằng nhau không? Giải thích vì sao.......

HĐ3 trang 49 Toán 12 Tập 1: Trong không gian, cho hai vectơ $\vec{a}$ và $\vec{b}$ không cùng phương. Lấy điểm A và vẽ các vectơ $\vec{A B} = \vec{a}, \vec{B C} = \vec{b}$ . Lấy điểm A’ và vẽ các vectơ $\vec{A^{'} B^{'}} = \vec{a}, \vec{B^{'} C^{'}} = \vec{b}$ (H.2.10).......

Luyện tập 3 trang 50 Toán 12 Tập 1: Trong Ví dụ 3, hãy tính độ dài của vectơ $\vec{A C} + \vec{C^{'} D^{'}}$ ......

Luyện tập 4 trang 50 Toán 12 Tập 1: Cho tứ diện ABCD (H.2.13). Chứng minh rằng $\vec{A B} + \vec{C D} = \vec{A D} + \vec{C B}$ .......

HĐ4 trang 50 Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’ (H.2.14)......

Câu hỏi trang 50 Toán 12 Tập 1: Trong Hình 2.14, hãy phát biểu quy tắc hình hộp với các vectơ có điểm đầu là B.....

Luyện tập 5 trang 50 Toán 12 Tập 1: Cho hình hộp hình chữ nhật ABCD.A’B’C’D’. Chứng minh rằng $\vec{B B^{'}} + \vec{C D} + \vec{A D} = \vec{B D^{'}}$ ......

HĐ5 trang 51 Toán 12 Tập 1: Hình 2.15 mô tả một lọ hoa được đặt trên bàn, trọng lượng của lọ hoa tạo nên một lực tác dụng lên mặt bàn và một phản lực từ mặt bàn lên lọ hoa. Có nhận xét về độ dài và hướng của các vectơ biểu diễn hai lực đó.......

Luyện tập 6 trang 52 Toán 12 Tập 1: Trong Ví dụ 6, chứng minh rằng:......

Vận dụng 2 trang 52 Toán 12 Tập 1: Thang cuốn tại các trung tâm thương mại, siêu thị hay nhà ga, sân bay thường có hai làn, trong đó một làn lên và một làn xuống. Khi thang cuốn chuyển động, vectơ biểu diễn vận tốc của mỗi làn có là hai vectơ đối nhau không? Giải thích vì sao.......

HĐ6 trang 52 Toán 12 Tập 1: Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M, N lần lượt là trung điểm của AB, AC (H.2.17)......

Câu hỏi trang 53 Toán 12 Tập 1: Hai vectơ $1 \vec{a}$ và $\vec{a}$ có bằng nhau không? Hai vectơ $(- 1) \vec{a}$ và $- \vec{a}$ có bằng nhau không?......

Luyện tập 7 trang 53 Toán 12 Tập 1: Cho hình chóp S. ABCD có đáy ABCD là hình bình hành. Gọi E, F lần lượt là các điểm thuộc các cạnh SA, SB sao cho $S E = \frac{1}{3} S A, S F = \frac{1}{3} S B$ . Chứng minh rằng $\vec{E F} = \frac{1}{3} \vec{D C}$ .......

Luyện tập 8 trang 54 Toán 12 Tập 1: Trong Ví dụ 8, gọi I là điểm thuộc đoạn thẳng AG sao cho $\vec{A I} = 3 \vec{I G}$ (H.2.19). Chứng minh rằng $\vec{I A} + \vec{I B} + \vec{I C} + \vec{I D} = \vec{0}$ .......

Vận dụng 3 trang 54 Toán 12 Tập 1: Khi chuyển động trong không gian, máy bay luôn chịu tác động của bốn lực chính: lực đẩy của động cơ, lực cản của không khí, trọng lực và lực nâng khí động học (H.2.20). Lực cản của không khí ngược hướng với lực đẩy của động cơ và có độ lớn tỉ lệ thuận với bình phương vận tốc máy bay. Một chiếc máy bay tăng vận tốc từ 900km/h lên 920km/h, trong quá trình tăng tốc máy bay giữ nguyên hướng bay. Lực cản của không khí khi máy bay đạt vận tốc 900km/h và 920km/h lần lượt được biểu diễn bởi hai vectơ $\vec{F_{1}}$ và $\vec{F_{2}}$ . Hãy giải thích vì sao $\vec{F_{1}} = k \vec{F_{2}}$ với k là một số thực dương nào đó. Tính giá trị của k (làm tròn kết quả đến chữ số thập phân thứ hai).......

HĐ7 trang 54 Toán 12 Tập 1: Trong không gian, cho hai vectơ $\vec{a}$ và $\vec{b}$ khác $\vec{0}$ . Lấy điểm O và vẽ các vectơ $\vec{O A} = \vec{a}, \vec{O B} = \vec{b}$ . Lấy điểm O’ khác O và vẽ các vectơ $\vec{O^{'} A^{'}} = \vec{a}, \vec{O^{'} B^{'}} = \vec{b}$ (H.2.21).......

Câu hỏi trang 55 Toán 12 Tập 1: Xác định góc giữa hai vectơ cùng hướng (và khác $\vec{0}$ ), góc giữa hai vectơ ngược hướng trong không gian......

Luyện tập 9 trang 56 Toán 12 Tập 1: Cho hình lăng trụ tam giác đều ABC.A’B’C’ (H.2.25). Tính các góc $(\vec{A A^{'}}, \vec{B C})$ và $(\vec{A B}, \vec{A^{'} C^{'}})$ .......

HĐ8 trang 56 Toán 12 Tập 1: Hãy nhắc lại công thức xác định tích vô hướng của hai vectơ trong mặt phẳng......

Luyện tập 10 trang 57 Toán 12 Tập 1: Trong Ví dụ 10, hãy tính các tích vô hướng $\vec{A S} . \vec{B D}$ và $\vec{A S} . \vec{C D}$ ......

Luyện tập 11 trang 57 Toán 12 Tập 1: Cho hình lập phương ABCD.A’B’C’D’. Chứng minh rằng $\vec{A^{'} C} . \vec{B^{'} D^{'}} = 0$ .......

Vận dụng 4 trang 57 Toán 12 Tập 1: Như đã biết, nếu có một lực $\vec{F}$ tác động vào một vật tại điểm M và làm cho vật đó di chuyển một quãng đường MN thì công A sinh ra được tính theo công thức $A = \vec{F} . \vec{M N}$ , trong đó lực F có độ lớn tính bằng Newton, quãng đường MN tính bằng mét và công A tính bằng Jun (H.2.28). Do đó, nếu dùng một lực $\vec{F}$ có độ lớn không đổi để làm một vật di chuyển một quãng đường không đổi thì công sinh ra sẽ lớn nhất khi lực tác động cùng hướng với chuyển động của vật. Hãy giải thích vì sao. Kết quả trên có thể được áp dụng như thế nào khi kéo (hoặc đẩy) các vật nặng?......

Bài 2.1 trang 58 Toán 12 Tập 1: Trong không gian, cho ba vectơ $\vec{a}, \vec{b}, \vec{c}$ phân biệt và đều khác $\vec{0}$ . Những mệnh đề nào sau đây là đúng?......

Bài 2.2 trang 58 Toán 12 Tập 1: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có $A B = 2, A D = 3$ và $A A^{'} = 4$ . Tính độ dài của các vectơ $\vec{B B^{'}}, \vec{B D}$ và $\vec{B D^{'}}$ .......

Bài 2.3 trang 58 Toán 12 Tập 1: Một chiếc bàn cân đối hình chữ nhật được đặt trên mặt sàn nằm ngang, mặt bàn song song với mặt sàn và bốn chân bàn vuông góc với mặt sàn như Hình 2.29. Trọng lực tác dụng lên bàn (biểu thị bởi vectơ $\vec{a}$ ) phân tán đều qua bốn chân bàn và gây nên các phản lực từ mặt sàn lên các chân bàn (biểu thị bởi các vectơ $\vec{b}, \vec{c}, \vec{d}, \vec{e}$ )........

Bài 2.4 trang 58 Toán 12 Tập 1: Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng:......

Bài 2.5 trang 58 Toán 12 Tập 1: Cho hình lăng trụ tam giác ABC.A’B’C’ có $\vec{A A^{'}} = \vec{a}, \vec{A B} = \vec{b}$ và $\vec{A C} = \vec{c}$ . Hãy biểu diễn các vectơ sau qua các vectơ $\vec{a}, \vec{b}, \vec{c}$ :.....

Bài 2.6 trang 58 Toán 12 Tập 1: Cho hình chóp tứ giác S. ABCD. Chứng minh rằng tứ giác ABCD là hình bình hành nếu và chỉ nếu $\vec{S A} + \vec{S C} = \vec{S B} + \vec{S D}$ . ......

Bài 2.7 trang 58 Toán 12 Tập 1: Cho hình chóp S.ABC. Trên cạnh SA, lấy điểm M sao cho $S M = 2 A M$ . Trên cạnh BC, lấy điểm N sao cho $C N = 2 B N$ . Chứng minh rằng $\vec{M N} = \frac{1}{3} (\vec{S A} + \vec{B C}) + \vec{A B}$ ......

Bài 2.8 trang 58 Toán 12 Tập 1: Trong Luyện tập 8, ta đã biết trọng tâm của tứ diện ABCD là một điểm I thỏa mãn $\vec{A I} = 3 \vec{I G}$ , ở đó G là trọng tâm của tam giác BCD. Áp dụng tính chất trên để tính khoảng cách từ trọng tâm của một khối rubik (đồng chất) hình tứ diện đều đến một mặt của nó, biết rằng chiều cao của khối rubik là 8cm (H.2.30).......

Bài 2.9 trang 59 Toán 12 Tập 1: Ba sợi dây không giãn với khối lượng không đáng kể được buộc chung một đầu và được kéo căng về ba hướng khác nhau (H.2.31). Nếu các lực kéo làm cho ba sợi dây ở trạng thái đứng yên thì khi đó ba sợi dây nằm trên cùng một mặt phẳng. Hãy giải thích vì sao......

Bài 2.10 trang 59 Toán 12 Tập 1: Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có độ dài mỗi cạnh đáy bằng 1 và độ dài mỗi cạnh bên bằng 2. Hãy tính góc giữa các cặp vectơ sau đây và tính tích vô hướng của mỗi cặp vectơ đó.....

Bài 2.11 trang 59 Toán 12 Tập 1: Trong không gian, cho hai vectơ $\vec{a}$ và $\vec{b}$ có cùng độ dài bằng 1. Biết rằng góc giữa hai vectơ đó là $45^{0}$ , hãy tính:......

Bài 2.12 trang 59 Toán 12 Tập 1: Cho tứ diện ABCD. Chứng minh rằng.....

Xem thêm các bài giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 1

Bài 6. Vectơ trong không gian

Bài 7. Hệ trục toạ độ trong không gian

Bài 8. Biểu thức toạ độ của các phép toán vectơ

Bài tập cuối chương 2

Bài 9. Khoảng biến thiên và khoảng tứ phân vị

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Tổng hợp kiến thức

Tia phân giác của một góc là gì? Tính chất tia phân giác của một góc

Tia phân giác của một góc là gì? Tính chất tia phân giác của một góc Van Anh

74

Toán Tổng hợp kiến thức

Đạo hàm của hàm số y = cos2x

Đạo hàm của hàm số y = cos2x Van Anh

76

Toán Tổng hợp kiến thức

Top 1000 Bài tập thường gặp môn Toán có đáp án (phần 110)

Top 1000 Bài tập thường gặp môn Toán có đáp án (phần 110) Minh Nguyệt

149

Toán Lớp 5

Vở bài tập Toán lớp 5 Tập 2 trang 130 Bài 91: Ôn tập chung | Cánh diều

Vở bài tập Toán lớp 5 Tập 2 trang 130 Bài 91: Ôn tập chung | Cánh diều Lữ Ngọc My My

98

Tìm kiếm

tailieugiaovien.com.vn

Bài Viết Xem Nhiều

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

© 2021 Vietjack. All Rights Reserved.