Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 12 Bài 7: Hệ trục toạ độ trong không gian chi tiết sách Toán 12 Tập 1 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 12. Mời các bạn đón xem:
Giải bài tập Toán 12 Bài 7: Hệ trục toạ độ trong không gian
1. Hệ trục tọa độ trong không gian
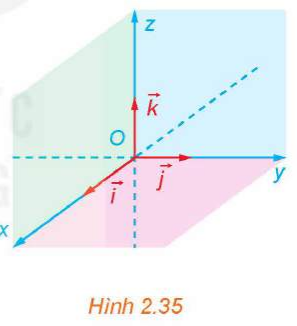
a) Gọi tên các mặt phẳng tọa độ có trong Hình 2.35.
b) Các mặt phẳng tọa độ trong Hình 2.35 có đôi một vuông góc với nhau không?
Lời giải:
a) Các mặt phẳng có trong hình vẽ là: Mặt phẳng (Oxy), (Oyz), (Ozx).
b) Vì , Ox và Oz cắt nhau tại O và nằm trong mặt phẳng (Oxz) nên . Mà
Chứng minh tương tự ta có:
Vậy ba mặt phẳng (Oxy), (Oyz), (Ozx) đôi một vuông góc với nhau.

Lời giải:
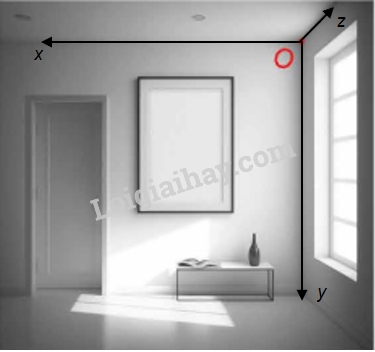
Góc căn phòng trong Hình 2.34 gợi lên hình ảnh về hệ trục tọa độ Oxyz trong không gian.
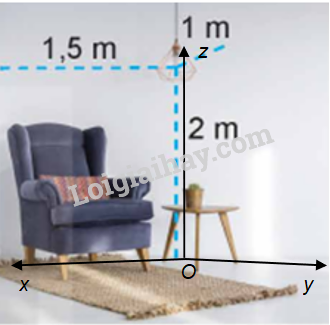
Mô tả: Hệ tọa độ Oxyz có:
+ Mặt phẳng (Oxy) là sàn nhà, hai mặt phẳng (Oyz), (Ozx) hai bức tường. Khi đó, ba mặt phẳng đôi một vuông góc với nhau.
+ Gốc tọa độ O (trùng với một góc phòng) là giao điểm của ba trục Ox, Oy, Oz.
Lời giải:
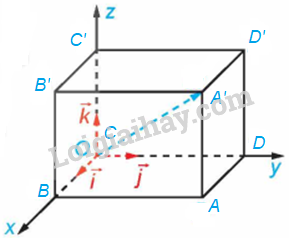
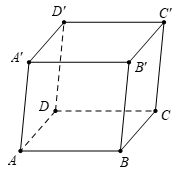
Vì ABCD. A’B’C’D’ là hình hộp chữ nhật nên các cạnh CC’, CB và CD đôi một vuông góc với nhau.
Các vectơ cùng có điểm đầu là C.
Do đó, suy ra có thể lập một hệ tọa độ Oxyz có gốc O trùng với đỉnh C và các vectơ lần lượt cùng hướng với các vectơ .
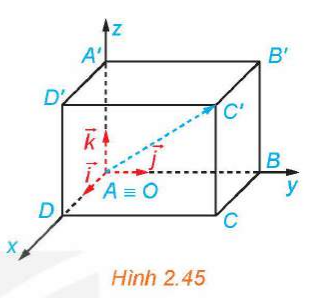
2. Tọa độ của điểm, tọa độ của vectơ trong không gian
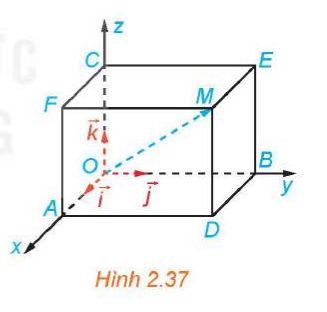
a) Hai vectơ và có bằng nhau hay không?
b) Giải thích vì sao có thể viết với x, y, z là các số thực.
Lời giải:
a) Vì OADB.CFME là hình hộp chữ nhật nên theo quy tắc hình hộp ta có:
b) Vì là vectơ đơn vị trên trục Ox nên với x là số thực.
Vì là vectơ đơn vị trên trục Oy nên với y là số thực.
Vì là vectơ đơn vị trên trục Oz nên với z là số thực.
Do đó, với x, y, z là các số thực.
Luyện tập 2 trang 62 Toán 12 Tập 1: Tìm tọa độ của điểm N trong Hình 2.39.
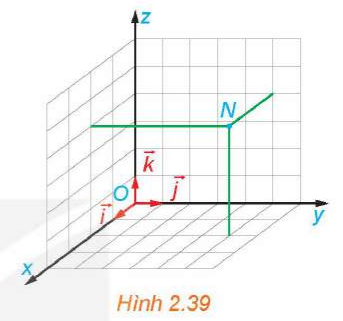
Lời giải:
Ta có: . Do đó, N(2; 5; 4).
Luyện tập 3 trang 62 Toán 12 Tập 1: Trong Ví dụ 3, hãy xác định tọa độ của các điểm B, D và C’.
Lời giải:
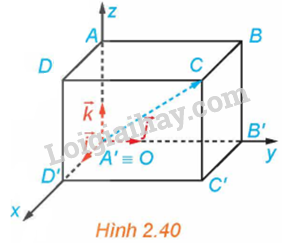
Theo Ví dụ 3 ta có: .
Vì ABB’O là hình bình hành nên . Do đó, B(0; 3; 5)
Vì OB’C’D’ là hình bình hành nên . Do đó, C’(2; 3; 0)
Vì ADD’A’ là hình bình hành nên . Do đó, D(2; 0; 5)
Trong Hình 2.34, một chiếc bóng đèn cách sàn nhà là 2m, cách hai bức tường lần lượt là 1m và 1,5m.

Lời giải:
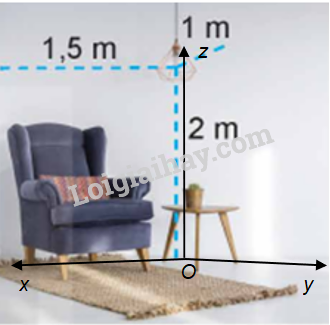
Mô tả: Hệ tọa độ Oxyz có:
+ Mặt phẳng (Oxy) là sàn nhà, hai mặt phẳng (Oyz), (Ozx) hai bức tường. Khi đó, ba mặt phẳng đôi một vuông góc với nhau.
+ Gốc tọa độ O (trùng với một góc phòng) là giao điểm của ba trục Ox, Oy, Oz.
Khi đó, bóng đèn có tọa độ (1,5; 1; 2).
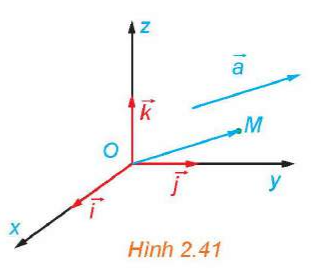
Lời giải:
Theo khái niệm tọa độ trong không gian ta có: . Mà nên . Do đó, có bộ ba số (x; y; z) sao cho .
Luyện tập 4 trang 63 Toán 12 Tập 1: Trong không gian Oxyz, hãy xác định tọa độ của vectơ .
Lời giải:
Tọa độ của vectơ là .
HĐ4 trang 63 Toán 12 Tập 1: Trong không gian Oxyz, cho hai điểm và .
a) Hãy biểu diễn hai vectơ và qua các vectơ và .
b) Xác định tọa độ của vectơ .
Lời giải:
a) Ta có: ,
b) Ta có:
Do đó, .
Lời giải:
Gọi tọa độ của điểm D là (x; y; z), tọa độ của D’ là , khi đó và .
Để ABCD.A’B’C’D’ là hình hộp thì ABCD là hình bình hành.
Do đó, . Suy ra
Để ABCD.A’B’C’D’ là hình hộp thì A’B’C’D’ là hình bình hành.
Do đó, . Suy ra

Lời giải:
Quãng đường máy bay bay được với vận tốc 890km/h trong nửa giờ là:
Vì máy bay duy trì hướng bay về phía nam nên tọa độ của vectơ biểu diễn độ dịch chuyển của chiếc máy bay trong nửa giờ đó với hệ tọa độ đã chọn là (0; 445; 0).
Bài tập
Bài 2.13 trang 64 Toán 12 Tập 1: Trong không gian Oxyz, cho ba vectơ , , đều khác và có giá đôi một vuông góc. Những mệnh đề nào sau đây là đúng?
a) Có thể lập được một hệ tọa độ Oxyz có các trục tọa độ lần lượt song song với giá của các vectơ , , .
b) Có thể lập được một hệ tọa độ Oxyz có các trục tọa độ lần lượt trùng với giá của các vectơ , , .
c) Có thể lập được một hệ tọa độ Oxyz có các vectơ lần lượt bằng các vectơ , , .
d) Có thể lập được một hệ tọa độ Oxyz có các vectơ lần lượt cùng phương các vectơ , , .
Lời giải:
Cả 4 câu đều đúng.

Lời giải:
Hình vẽ phù hợp với mô tả:
Bài 2.15 trang 65 Toán 12 Tập 1: Trong không gian Oxyz, xác định tọa độ của vectơ trong mỗi trường hợp sau:
a) và ;
b) và ;
c) và .
Lời giải:
a)
b)
c)
Bài 2.16 trang 65 Toán 12 Tập 1: Trong không gian Oxyz, xác định tọa độ của điểm A trong mỗi trường hợp sau:
a) A trùng với gốc tọa độ;
b) A nằm trên tia Ox và ;
c) A nằm trên tia đối của tia Oy và .
Lời giải:
a) A trùng với gốc tọa độ nên A(0; 0; 0).
b) Vì A nằm trên tia Ox và nên . Do đó, A(2; 0; 0).
c) Vì A nằm trên tia đối của tia Oy và nên . Do đó, .
Lời giải:
Vì A trùng gốc O nên A(0; 0; 0).
Vì D thuộc tia Ox nên hai vectơ và cùng hướng. Do đó, tồn tại số thực m sao cho . Mà D(2; 0; 0) nên .
Vì B thuộc tia Oy nên hai vectơ và cùng hướng. Do đó, tồn tại số thực n sao cho . Mà B(0; 4; 0) nên
Vì A’ thuộc tia Oz nên hai vectơ và cùng hướng. Do đó, tồn tại số thực p sao cho . Mà A’(0; 0; 3) nên .
Vì ODCB là hình bình hành nên . Do đó, C(2; 4; 0).
Vì OA’B’B là hình bình hành nên . Do đó, B’(0; 4; 3).
Vì OA’D’D là hình bình hành nên . Do đó, D’(2; 0; 3).
Vì ABCD. A’B’C’D’ là hình hộp chữ nhật nên theo quy tắc hình hộp ta có:
. Do đó, C’(2; 4; 3).
a) Xác định tọa độ của điểm C.
b) Xác định các tọa độ đỉnh còn lại của hình hộp.
Lời giải:
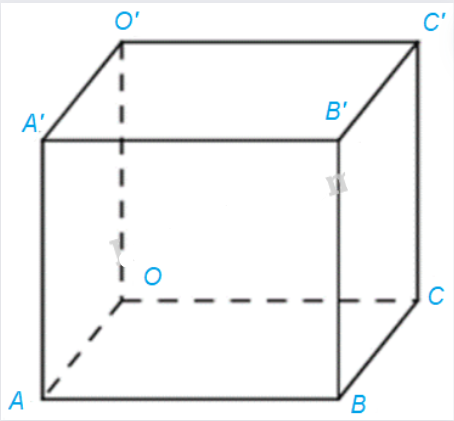
a) Ta có: O(0; 0; 0)
Vì OABC.O’A’B’C’ là hình hộp nên AOBC là hình bình hành. Do đó:
b) Vì OABC.O’A’B’C’ là hình hộp nên
Lời giải:
Khi máy bay di chuyển trên đường băng, tức là máy bay di chuyển ở trên mặt đất, tức là thuộc mặt phẳng (Oxy). Do đó, máy bay khi di chuyển trên đường băng thì tọa độ của nó luôn có dạng (x; y; 0) với x, y là hai số thực nào đó.

Xem thêm các bài giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:
Bài 7. Hệ trục toạ độ trong không gian
Bài 8. Biểu thức toạ độ của các phép toán vectơ
Bài 9. Khoảng biến thiên và khoảng tứ phân vị
Bài 10. Phương sai và độ lệch chuẩn
Lý thuyết Hệ trục toạ độ trong không gian
1. Hệ trục tọa độ trong không gian
|
Trong không gian, ba trục Ox, Oy, Oz đôi một vuông góc với nhau tại gốc O của mỗi trục. Gọi lần lượt là các vecto đơn vị trên các trục Ox, Oy, Oz - Hệ ba trục như vậy được gọi là hệ trục tọa độ Descartes vuông góc Oxyz, hay đơn giản là hệ tọa độ Oxyz - Điểm O được gọi là gốc tọa độ - Các mặt phẳng (Oxy), (Oyz), (Oxz) đôi một vuông góc với nhau được gọi là các mặt phẳng tọa độ Không gian với hệ tọa độ Oxyz còn được gọi là không gian Oxyz |
2. Tọa độ của điểm, tọa độ của vecto trong không gian
Tọa độ của điểm
|
Trong không gian Oxyz, cho một điểm M tùy ý. Bộ ba số (x;y;z) duy nhất sao cho được gọi là tọa độ của điểm M đối với hệ tọa độ Oxyz. Khi đó, ta viết M = (x,y,z), trong đó x là hoành độ, y là tung độ và z là cao độ của M |
Tọa độ của vecto
|
Trong không gian Oxyz, cho vecto tùy ý. Bộ ba số (x;y;z) duy nhất sao cho được gọi là tọa độ của vecto đối với hệ tọa độ Oxyz. Khi đó, ta viết = (x,y,z) hoặc (x,y,z) Trong không gian Oxyz, cho hai điểm và . Khi đó:
|
Ví dụ: Trong không gian Oxyz, cho hình lăng trụ tam giác ABC.A’B’C có A(1;0;2), B(3;2;5), C(7;-3;9)
a) Tìm tọa độ của
b) Tìm tọa độ của các điểm B’, C’
Lời giải
a) Ta có:
b) Gọi tọa độ của điểm B’ là (x,y,z) thì = (x-3;y-2;z-5). Vì ABC.A’B’C’ là hình lăng trụ nên ABB’A’ là hình bình hành, suy ra =
Do đó hay x = 7, y = 2, z = 4. Vậy B’(7;2;4)
Lập luận tương tự suy ra C’(11;-3;8)