Với giải Bài 1.15 trang 23 Toán 9 Tập 1 Kết nối tri thức chi tiết trong Bài 3: Giải bài toán bằng cách lập hệ phương trình giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 9. Mời các bạn đón xem:
Giải bài tập Toán 9 Bài 3: Giải bài toán bằng cách lập hệ phương trình
Bài 1.15 trang 23 Toán 9 Tập 1: Tìm số tự nhiên N có hai chữ số, biết rằng tổng của hai chữ số đó bằng 12, và nếu viết hai chữ số đó theo thứ tự ngược lại thì được một số lớn hơn N là 36 đơn vị.
Lời giải:
Gọi chữ số N cần tìm có dạng
Tổng của hai chữ số đó bằng 12 nên ta có phương trình
Hai chữ số viết theo thứ tự ngược lại ta được số mới có dạng
Ta được số mới lớn hơn số đã cho là 36 đơn vị nên ta có phương trình
Nên suy ra hay
Từ đó ta có hệ phương trình
Cộng từng vế của hai phương trình ta có hay nên
Thay vào phương trình thứ nhất ta có nên
Vậy số N cần tìm là 48
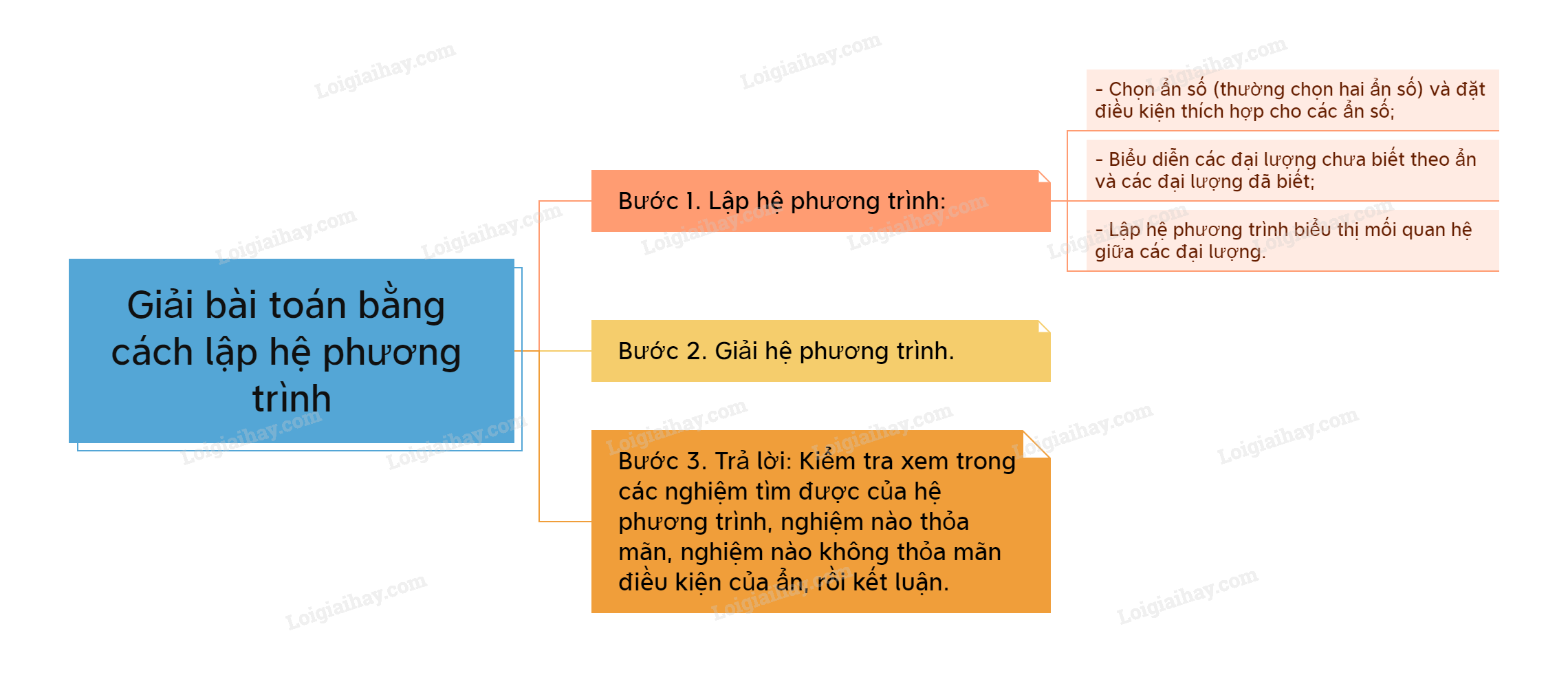
Sơ đồ tư duy Giải bài toán bằng cách lập hệ phương trình
Xem thêm lời giải bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:
Xem thêm các bài giải bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:
Bài 3. Giải bài toán bằng cách lập hệ phương trình
Bài 4. Phương trình quy về phương trình bậc nhất một ẩn
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
