Tailieumoi.vn giới thiệu Giải bài tập Toán lớp 12 Bài 13: Ứng dụng hình học của tích phân chi tiết sách Toán 12 Tập 2 Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 12. Mời các bạn đón xem:

Giải bài tập Toán 12 Bài 13: Ứng dụng hình học của tích phân 

HĐ1 trang 19 Toán 12 Tập 2: Xét hình phẳng giới hạn bởi đường thẳng y = f(x) = x + 1, trục hoành và hai đường thẳng x = −2; x = 1 (H.4.12).

a) Tính diện tích S của hình phẳng này.

b) Tính $\underset{-2}{\overset{1}{\int }}\left|f\left(x\right)\right|dx$ và so sánh với S.

Lời giải:

a)

Gọi A(−2; 0), C(−1; 0), D(1; 0) và B, E lần lượt là giao điểm của đường thẳng x = −2, x = 1 với đường thẳng y = x + 1.

Do đó B(−2; −1), E(1; 2).

Khi đó S = S_∆ABC + S_∆CDE = $\frac{1}{2}AB.AC+\frac{1}{2}CD.DE$$=\frac{1}{2}\mathrm{.1.1}+\frac{1}{2}\mathrm{.2.2}=\frac{5}{2}$

b) $\underset{-2}{\overset{1}{\int }}\left|f\left(x\right)\right|dx$$=\underset{-2}{\overset{1}{\int }}\left|x+1\right|dx$$=\underset{-2}{\overset{-1}{\int }}\left|x+1\right|dx+\underset{-1}{\overset{1}{\int }}\left|x+1\right|dx$$=-\underset{-2}{\overset{-1}{\int }}\left(x+1\right)dx+\underset{-1}{\overset{1}{\int }}\left(x+1\right)dx$

$=-{\left.\left(\frac{x^2}{2}+x\right)\right|}_{-2}^{-1}+{\left.\left(\frac{x^2}{2}+x\right)\right|}_{-1}^1$$=\frac{1}{2}+\frac{3}{2}+\frac{1}{2}=\frac{5}{2}$

Vậy $S=\underset{-2}{\overset{1}{\int }}\left|f\left(x\right)\right|dx$

Luyện tập 1 trang 20 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi parabol y = x² – 4, trục hoành và hai đường thẳng x = 0; x = 3 (H.4.15).

Lời giải:

Diện tích hình phẳng cần tính là:

$\underset{0}{\overset{3}{\int }}\left|x^2-4\right|dx$$=\underset{0}{\overset{2}{\int }}\left|x^2-4\right|dx+\underset{2}{\overset{3}{\int }}\left|x^2-4\right|dx$$=\underset{0}{\overset{2}{\int }}\left(4-x^2\right)dx+\underset{2}{\overset{3}{\int }}\left(x^2-4\right)dx$

$={\left.\left(4x-\frac{x^3}{3}\right)\right|}_0^2+{\left.\left(\frac{x^3}{3}-4x\right)\right|}_2^3$$=\frac{16}{3}-3+\frac{16}{3}=\frac{23}{3}$

HĐ2 trang 20 Toán 12 Tập 2: Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của các hàm số f(x) = −x² + 4x, g(x) = x và hai đường thẳng x = 1, x = 3 (H.4.16).

a) Giả sử S₁ là diện tích hình phẳng giới hạn bởi parabol y = −x² + 4x, trục hoành và hai đường thẳng x = 1, x = 3; S₂ là diện tích hình phẳng giới hạn bởi đường thẳng y = x, trục hoành và hai đường thẳng x = 1, x = 3. Tính S₁, S₂ và từ đó suy ra S.

b) Tính $\underset{1}{\overset{3}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx$ và so sánh với S.

Lời giải:

a) Ta có $S_1=\underset{1}{\overset{3}{\int }}\left|-x^2+4x\right|dx$$=\underset{1}{\overset{3}{\int }}\left(-x^2+4x\right)dx$$={\left.\left(-\frac{x^3}{3}+2x^2\right)\right|}_1^3$$=9-\frac{5}{3}=\frac{22}{3}$

$S_2=\underset{1}{\overset{3}{\int }}\left|x\right|dx$$=\underset{1}{\overset{3}{\int }}xdx$$={\left.\frac{x^2}{2}\right|}_1^3=\frac{9}{2}-\frac{1}{2}=4$

Do đó S = S₁ – S₂ = $\frac{22}{3}-4=\frac{10}{3}$

b) $\underset{1}{\overset{3}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx$$=\underset{1}{\overset{3}{\int }}\left|-x^2+4x-x\right|dx$$=\underset{1}{\overset{3}{\int }}\left|-x^2+3x\right|dx$

$=\underset{1}{\overset{3}{\int }}\left(-x^2+3x\right)dx$$={\left.\left(-\frac{x^3}{3}+3.\frac{x^2}{2}\right)\right|}_1^3$$=\frac{9}{2}-\frac{7}{6}=\frac{10}{3}$

Vậy $S=\underset{1}{\overset{3}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx$

Luyện tập 2 trang 21 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số $y=\sqrt{x}$, y = x – 2 và hai đường thẳng x = 1, x = 4.

Lời giải:

Diện tích hình phẳng cần tính là:

$S=\underset{1}{\overset{4}{\int }}\left|\sqrt{x}-x+2\right|dx$$=\underset{1}{\overset{4}{\int }}\left(\sqrt{x}-x+2\right)dx$$={\left.\left(\frac{2}{3}{x}^{\frac{3}{2}}-\frac{x^2}{2}+2x\right)\right|}_1^4$$=\frac{16}{3}-\frac{13}{6}=\frac{19}{6}$

Vận dụng 1 trang 22 Toán 12 Tập 2: Ta biết rằng hàm cầu liên quan đến giá p của một sản phẩm với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm với mức độ sẵn sàng cung cấp sản phẩm của nhà sản xuất. Điểm cắt nhau (x₀; p₀) của đồ thị hàm cầu p = D(x) và đồ thị hàm cung p = S(x) được gọi là điểm cân bằng.

Các nhà kinh tế gọi diện tích của hình giới hạn bởi đồ thị hàm cầu, đường ngang p = p₀ và đường thẳng đứng x = 0 là thặng dư tiêu dùng. Tương tự, diện tích của hình giới hạn bởi đồ thị của hàm cung, đường nằm ngang p = p₀ và đường thẳng đứng x = 0 được gọi là thặng dư sản xuất, như trong Hình 4.19.

(Theo R.Larson, Brief Calculus: An Applied Approach, 8^th edition, Cengage Learning, 2009).

Giả sử hàm cung và hàm cầu của một loại sản phẩm được mô hình hóa bởi:

Hàm cầu: p = −0,36x + 9 và hàm cung: p = 0,14x + 2, trong đó x là số đơn vị sản phẩm. Tìm thặng dư tiêu dùng và thặng dư sản xuất cho sản phẩm này.

Lời giải:

Hoành độ điểm cân bằng là nghiệm của phương trình:

−0,36x + 9 = 0,14x + 2 ⇔ x = 14.

Tọa độ điểm cân bằng là (14; 3,96).

Thặng dư tiêu dùng là:

$S_1=\underset{0}{\overset{14}{\int }}\left|-\mathrm{0,36}x+9-\mathrm{3,96}\right|dx$$=\underset{0}{\overset{14}{\int }}\left|-\mathrm{0,36}x+\mathrm{5,04}\right|dx$

$=\underset{0}{\overset{14}{\int }}\left(-\mathrm{0,36}x+\mathrm{5,04}\right)dx$

Thặng dư sản xuất là:

$S_2=\underset{0}{\overset{14}{\int }}\left|\mathrm{3,96}-\mathrm{0,14}x-2\right|dx$$=\underset{0}{\overset{14}{\int }}\left|\mathrm{1,96}-\mathrm{0,14}x\right|dx$

$=\underset{0}{\overset{14}{\int }}\left(\mathrm{1,96}-\mathrm{0,14}x\right)dx$$={\left.\left(\mathrm{1,96}x-\mathrm{0,07}{x}^2\right)\right|}_0^{14}$=13,72

HĐ3 trang 22 Toán 12 Tập 2: Xét hình trụ có bán kính đáy R, có trục là trục hoành Ox, nằm giữa hai mặt phẳng x = a và x = b (a < b) (H.4.20).

a) Tính thể tích V của hình trụ.

b) Tính diện tích mặt cắt S(x) khi cắt hình trụ bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x (a ≤ x ≤ b). Từ đó tính $\underset{a}{\overset{b}{\int }}S\left(x\right)dx$ và so sánh với V.

Lời giải:

a) Độ dài chiều cao hình trụ là: h = b – a.

Thể tích của hình trụ là: V = πR²h = πR²(b – a).

b) Diện tích mặt cắt S(x) khi cắt hình trụ bởi mặt phẳng vuông góc với trục Ox là

S(x) = πR².

Ta có $\underset{a}{\overset{b}{\int }}S\left(x\right)dx$$=\underset{a}{\overset{b}{\int }}\pi R^{2}dx$$={\left.\left(\pi R^{2}x\right)\right|}_a^b$$=\pi R^2\left(b-a\right)$

Vậy $V=\underset{a}{\overset{b}{\int }}S\left(x\right)dx$

Vận dụng 2 trang 23 Toán 12 Tập 2: Tính thể tích của khối chóp cụt đều có diện tích hai đáy là S₀, S₁ và chiều cao bằng h (H.4.24). Từ đó suy ra công thức tính thể tích khối chóp đều có diện tích đáy bằng S và chiều cao bằng h.

Lời giải:

Chọn hệ trục tọa độ Oxyz như hình vẽ.

Gọi a, b lần lượt là khoảng cách từ O đến đáy nhỏ và đáy lớn của hình chóp. Khi đó chiều cao của hình chóp cụt là h = b – a.

Thiết diện của khối chóp cụt khi cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x (a ≤ x ≤ b) là một đa giác đều đồng dạng với đáy lớn của hình chóp cụt theo tỉ số đồng dạng là $\frac{x}{b}$

Khi đó $\frac{S\left(x\right)}{S_1}=\frac{x^2}{b^2}\Rightarrow S\left(x\right)=\frac{x^2}{b^2}.S_1$

Do đó thể tích khối chóp cụt đều là:

$V=\underset{a}{\overset{b}{\int }}S\left(x\right)dx=\underset{a}{\overset{b}{\int }}\frac{x^2}{b^2}{S}_{1}dx={\left.\frac{S_1}{b^2}.\frac{x^3}{3}\right|}_a^b$$=\frac{S_1}{3b^2}\left(b^3-a^3\right)$

$=\frac{b-a}{3b^2}.\left(S_1{b}^2+S_{1}ab+S_1{a}^2\right)$$=\frac{h}{3}.\left[S_1+S_1\frac{a}{b}+S_1{\left(\frac{a}{b}\right)}^2\right]$

Vì $\frac{S_0}{S_1}={\left(\frac{a}{b}\right)}^2\Rightarrow S_0=S_1.{\left(\frac{a}{b}\right)}^2$; $S_0{S}_1=S_1^2.{\left(\frac{a}{b}\right)}^2$$\Rightarrow \sqrt{S_0{S}_1}=S_1.\frac{a}{b}$

Do đó $V=\frac{h}{3}.\left[S_1+\sqrt{S_1.S_0}+S_0\right]$

Khối chóp đều được coi là khối chóp cụt đều khi S₀ = 0.

Do đó thể tích khối chóp đều là $V=\frac{1}{3}.S.h$

HĐ4 trang 24 Toán 12 Tập 2: Xét hình phẳng giới hạn bởi đồ thị hàm số $f\left(x\right)=\frac{1}{2}x$, trục hoành và hai đường thẳng x = 0, x = 4. Khi quay hình phẳng này xung quanh trục hoành Ox ta được khối nón có đỉnh là gốc O, trục là Ox và đáy là hình tròn bán kính bằng 2 (H.4.25).

a) Tính thể tích V của khối nón.

b) Chứng minh rằng khi cắt khối nón bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ bằng x (0 ≤ x ≤ 4) thì mặt cắt thu được là một hình tròn có bán kính là f(x), do đó diện tích mặt cắt là S(x) = πf²(x). Tính $\pi \underset{0}{\overset{4}{\int }}{f}^2\left(x\right)dx$ và so sánh với V.

Lời giải:

a) Ta có chiều cao của khối nón là h = 4, bán kính đáy của khối nón là R = 2.

Do đó thể tích của khối nón là $V=\frac{1}{3}\pi R^{2}h=\frac{1}{3}\pi {.2}^2.4=\frac{16\pi }{3}$

b)

Khi cắt khối nón bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ bằng x (0 ≤ x ≤ 4) thì mặt cắt thu được là một hình tròn có bán kính là $f\left(x\right)=\frac{1}{2}x$

Khi đó diện tích mặt cắt là $S\left(x\right)=\pi f^2\left(x\right)=\frac{\pi }{4}{x}^2$

Ta có $\pi \underset{0}{\overset{4}{\int }}{f}^2\left(x\right)dx$$=\pi \underset{0}{\overset{4}{\int }}\frac{x^2}{4}dx$$=\frac{\pi }{4}\underset{0}{\overset{4}{\int }}{x}^{2}dx$$={\left.\left(\frac{\pi }{4}.\frac{x^3}{3}\right)\right|}_0^4=\frac{16\pi }{3}$

Vậy $V=\pi \underset{0}{\overset{4}{\int }}{f}^2\left(x\right)dx$

Vận dụng 3 trang 25 Toán 12 Tập 2: a) Tính thể tích của khối tròn xoay sinh ra khi quay hình thang vuông OABC trong mặt phẳng Oxy với OA = h, AB = R và OC = r, quanh trục Ox (H.4.28).

b) Từ công thức thu được ở phần a, hãy rút ra công thức tính thể tích của khối nón có bán kính đáy bằng R và chiều cao h.

Lời giải:

a) Chọn hệ trục như hình vẽ.

Khi đó ta có C(0; r), B(h; R). Suy ra $\overrightarrow{BC}=\left(h;R-r\right)$

Phương trình đường thẳng BC qua C và nhận $\overrightarrow{n}=\left(r-R;h\right)$ có dạng:

(r – R)x + h(y − r) = 0 hay $y=\frac{hr+\left(R-r\right)x}{h}$

Thể tích cần tính là:

$V=\pi \underset{0}{\overset{h}{\int }}{\left[\frac{hr+\left(R-r\right)x}{h}\right]}^{2}dx$$=\pi \underset{0}{\overset{h}{\int }}\left[r^2+2r.\frac{R-r}{h}x+{\left(\frac{R-r}{h}x\right)}^2\right]dx$

$=\pi {\left.\left(r^{2}x+r.\frac{R-r}{h}.x^2+{\left(\frac{R-r}{h}\right)}^2.\frac{x^3}{3}\right)\right|}_0^h$$=\pi \left[r^{2}h+\left(Rr-r^2\right).h+\frac{{\left(R-r\right)}^2.h}{3}\right]$

$=\pi \left(r^{2}h+Rrh-r^{2}h+\frac{1}{3}{R}^{2}h-\frac{2}{3}Rrh+\frac{1}{3}{r}^{2}h\right)$$=\pi \left(\frac{1}{3}{R}^{2}h+\frac{1}{3}Rrh+\frac{1}{3}{r}^{2}h\right)$

$=\frac{1}{3}\pi h\left(R^2+Rr+r^2\right)$

b) Khi r = 0 thì khối nón cụt trở thành khối nón có chiều cao h, bán kính đáy là R.

Do đó $V=\frac{1}{3}\pi R^{2}h$

Bài 4.14 trang 25 Toán 12 Tập 2: Tính diện tích của hình phẳng được tô màu trong Hình 4.29.

Lời giải:

Diện tích cần tính là:

$S=\underset{0}{\overset{4}{\int }}\left|5x-x^2-x\right|dx$$=\underset{0}{\overset{4}{\int }}\left|4x-x^2\right|dx$

$=\underset{0}{\overset{4}{\int }}\left(4x-x^2\right)dx$$={\left.\left(2x^2-\frac{x^3}{3}\right)\right|}_0^4$$=\frac{32}{3}$

Bài 4.15 trang 25 Toán 12 Tập 2: Tính diện tích của hình phẳng giới hạn bởi các đường:

a) y = e^x, y = x² – 1, x = −1, x = 1;

b) y = sinx, y = x, $x=\frac{\pi }{2},x=\pi$;

c) y = 9 – x², y = 2x², $x=-\sqrt{3},x=\sqrt{3}$;

d) $y=\sqrt{x},$ y = x², x = 0, x = 1.

Lời giải:

a)

Diện tích cần tính là:

$S=\underset{-1}{\overset{1}{\int }}\left|e^x-x^2+1\right|dx$$=\underset{-1}{\overset{1}{\int }}\left(e^x-x^2+1\right)dx$

$={\left.\left(e^x-\frac{x^3}{3}+x\right)\right|}_{-1}^1$$=e+\frac{2}{3}-e^{-1}+\frac{2}{3}$$=\frac{e^2-1}{e}+\frac{4}{3}$

b) Diện tích cần tính là:

$S=\underset{\frac{\pi }{2}}{\overset{\pi }{\int }}\left|\sin x-x\right|dx$$=\underset{\frac{\pi }{2}}{\overset{\pi }{\int }}\left(x-\sin x\right)dx$

$={\left.\left(\frac{x^2}{2}+\cos x\right)\right|}_{\frac{\pi }{2}}^{\pi }$$=\frac{{\pi }^2}{2}-1-\frac{{\pi }^2}{8}=\frac{3{\pi }^2}{8}-1$

c)

Diện tích cần tính là:

$S=\underset{-\sqrt{3}}{\overset{\sqrt{3}}{\int }}\left|9-x^2-2x^2\right|dx$$=\underset{-\sqrt{3}}{\overset{\sqrt{3}}{\int }}\left|9-3x^2\right|dx$$=\underset{-\sqrt{3}}{\overset{\sqrt{3}}{\int }}\left(9-3x^2\right)dx$

$={\left.\left(9x-x^3\right)\right|}_{-\sqrt{3}}^{\sqrt{3}}$$=9\sqrt{3}-3\sqrt{3}+9\sqrt{3}-3\sqrt{3}$$=12\sqrt{3}$

d)

Diện tích cần tính là:

$S=\underset{0}{\overset{1}{\int }}\left|\sqrt{x}-x^2\right|dx$$=\underset{0}{\overset{1}{\int }}\left(\sqrt{x}-x^2\right)dx$$={\left.\left(\frac{2}{3}{x}^{\frac{3}{2}}-\frac{x^3}{3}\right)\right|}_0^1$$=\frac{1}{3}$

Bài 4.16 trang 25 Toán 12 Tập 2: Các nhà kinh tế sử dụng đường cong Lorenz để minh họa sự phân phối thu nhập trong một quốc gia. Gọi x là đại diện cho phần trăm số gia đình trong một quốc gia và y là phần trăm tổng thu nhập, mô hình y = x sẽ đại diện cho một quốc gia mà các gia đình có thu nhập như nhau. Đường cong Lorenz y = f(x), biểu thị phân phối thu nhập thực tế. Diện tích giữa hai mô hình này, với 0 ≤ x ≤ 100, biểu thị “sự bất bình đẳng về thu nhập” của một quốc gia. Năm 2005, đường con Lorenz của Hoa Kỳ có thể được mô hình hóa bởi hàm số

y = (0,00061x² + 0,0218x + 1723)², 0 ≤ x ≤ 100,

trong đó x được tính từ các gia đình nghèo nhất đến giàu có nhất (Theo R.Larson, Brief Calculus: An Applied Approach, 8^th edition, Cengage Learning, 2009).

Tìm sự bất bình đẳng thu nhập của Hoa Kỳ vào năm 2005.

Lời giải:

Sự bất bình đẳng thu nhập của Hoa Kỳ vào năm 2005 là:

$S=\underset{0}{\overset{100}{\int }}\left|{\left(\mathrm{0,00061}{x}^2+\mathrm{0,0218}x+1723\right)}^2-x\right|dx$

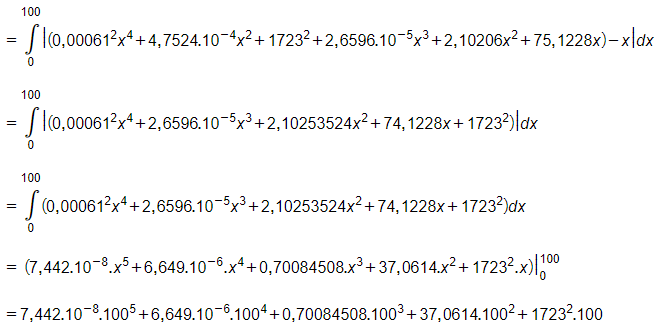
= 297945768,2.

Bài 4.17 trang 26 Toán 12 Tập 2: Tính thể tích của khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường sau xung quanh trục Ox: y = 2x – x², y = 0, x = 0, x = 2.

Lời giải:

Thể tích cần tìm là:

$V=\pi \underset{0}{\overset{2}{\int }}{\left(2x-x^2\right)}^{2}dx$$=\pi \underset{0}{\overset{2}{\int }}\left(4x^2-4x^3+x^4\right)dx$$=\pi {\left.\left(\frac{4}{3}{x}^3-x^4+\frac{x^5}{5}\right)\right|}_0^2$$=\frac{16\pi }{15}$

Bài 4.18 trang 26 Toán 12 Tập 2: Khối chỏm cầu có bán kính R và chiều cao h (0 < h ≤ R) sinh ra khi quay hình phẳng giới hạn bởi cung tròn có phương trình $y=\sqrt{R^2-x^2}$, trục hoành và hai đường thẳng x = R – h, x = R xung quanh trục Ox (H.4.30). Tính thể tích của khối chỏm cầu này.

Lời giải:

Thể tích cần tìm là:

$V=\pi \underset{R-h}{\overset{R}{\int }}\left(R^2-x^2\right)dx$$=\pi {\left.\left(R^{2}x-\frac{x^3}{3}\right)\right|}_{R-h}^R$

$=\pi \left(R^3-\frac{R^3}{3}-R^2\left(R-h\right)+\frac{{\left(R-h\right)}^3}{3}\right)$

$=\pi \left(R^3-\frac{R^3}{3}-R^3+R^{2}h+\frac{R^3}{3}-R^{2}h+R{h}^2-\frac{h^3}{3}\right)$

$=\pi \left(R{h}^2-\frac{h^3}{3}\right)$$=\pi h^2\left(R-\frac{h}{3}\right)$

Bài 4.19 trang 26 Toán 12 Tập 2: Cho tam giác vuông OAB có cạnh OA = a nằm trên trục Ox và $\widehat{AOB}=\alpha \left(0<\alpha \le \frac{\pi }{4}\right)$. Gọi β là khối tròn xoay sinh ra khi quay miền tam giác OAB xung quanh trục Ox (H.4.31).

a) Tính thể tích V của β theo a và α.

b) Tìm α sao cho thể tích V lớn nhất

Lời giải:

a) Xét tam giác OAB vuông tại A, có AB = OA.tanα = a.tanα.

Khi quay miền tam giác OAB xung quanh trục Ox ta được khối nón có bán kính đáy r = AB = a.tanα và chiều cao h = OA = a.

Do đó $V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\pi a^3{\tan }^2\alpha$

b) Có $V^{\text{'}}=\frac{1}{3}\pi a^3.2\tan \alpha .\frac{1}{{\cos }^2\alpha }$

Vì $0<\alpha \le \frac{\pi }{4}$ => 0 < tanα ≤ 1 nên V' > 0. Do đó V là hàm số đồng biến trên $\left(0;\frac{\pi }{4}\right)$

Do đó $\underset{\left(0;\frac{\pi }{4}\right]}{\max }V=V\left(\frac{\pi }{4}\right)=\frac{1}{3}\pi a^3$

Vậy $\alpha =\frac{\pi }{4}$ thì thể tích khối nón là lớn nhất.

Xem thêm các bài giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

Bài 12. Tích phân

Bài 13. Ứng dụng hình học của tích phân

Bài tập cuối chương 4

Bài 14. Phương trình mặt phẳng

Bài 15. Phương trình đường thẳng trong không gian

Bài 16. Công thức tính góc trong không gian